24.5: The Isolobal Principle and Application of Wade's Rules
- Page ID
- 34569
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ken Wade developed a method for the prediction of shapes of borane clusters; however, it may be used for a wide range of substituted boranes (such as carboranes) as well as other classes of cluster compounds. Wade’s rules are used to rationalize the shape of borane clusters by calculating the total number of skeletal electron pairs (SEP) available for cluster bonding. In using Wade’s rules it is key to understand structural relationship of various boranes.
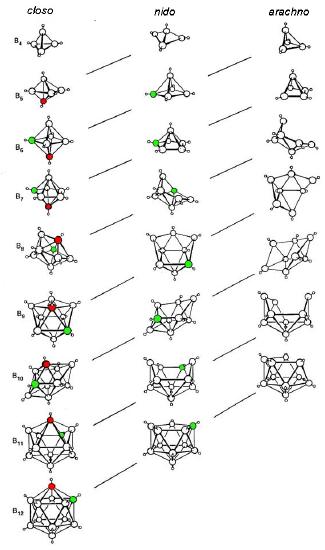
Structural relationship between closo, nido, and arachno boranes (and hetero-substituted boranes). The diagonal lines connect species that have the same number of skeletal electron pairs (SEP). Hydrogen atoms except those of the B-H framework are omitted. The red atom is omitted first, the green atom removed second. Adapted from R. W. Rudolph, Acc. Chem. Res., 1976, 9, 446.
The general methodology to be followed when applying Wade’s rules is as follows:
- Determine the total number of valence electrons from the chemical formula, i.e., 3 electrons per B, and 1 electron per H.
- Subtract 2 electrons for each B-H unit (or C-H in a carborane).
- Divide the number of remaining electrons by 2 to get the number of skeletal electron pairs (SEP).
- A cluster with n vertices (i.e., n boron atoms) and n+1 SEP for bonding has a closo structure.
- A cluster with n-1 vertices (i.e., n-1 boron atoms) and n+1 SEP for bonding has a nido structure.
- A cluster with n-2 vertices (i.e., n-2 boron atoms) and n+1 SEP for bonding has an arachno structure.
- A cluster with n-3 vertices (i.e., n-3 boron atoms) and n+1 SEP for bonding has an hypho structure.
- If the number of boron atoms (i.e., n) is larger than n+1 SEP then the extra boron occupies a capping position on a triangular phase.
What is the structure of B5H11?
Solution
- Total number of valence electrons = (5 x B) + (11 x H) = (5 x 3) + (11 x 1) = 26
- Number of electrons for each B-H unit = (5 x 2) = 10
- Number of skeletal electrons = 26 – 10 = 16
- Number SEP = 16/2 = 8
- If n+1 = 8 and n-2 = 5 boron atoms, then n = 7
- Structure of n = 7 is pentagonal bipyramid, therefore B5H11 is an arachno based upon a pentagonal bipyramid with two apexes missing.
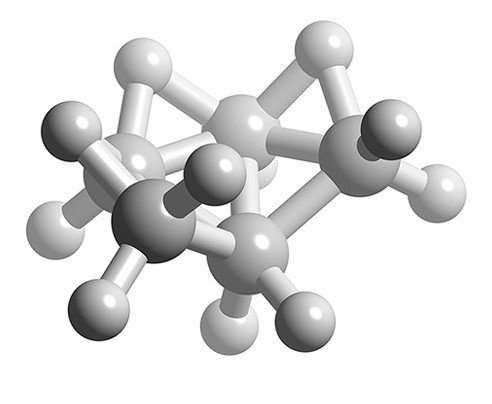
Ball and stick representation of the structure of B5H11.
What is the structure of B5H9?
Solution
- Total number of valence electrons = (5 x B) + (9 x H) = (5 x 3) + (9 x 1) = 24
- Number of electrons for each B-H unit = (5 x 2) = 10
- Number of skeletal electrons = 24 – 10 = 14
- Number SEP = 14/2 = 7
- If n+1 = 7 and n-1 = 5 boron atoms, then n = 6
- Structure of n = 6 is octahedral, therefore B5H9 is a nido structure based upon an octahedral structure with one apex missing.
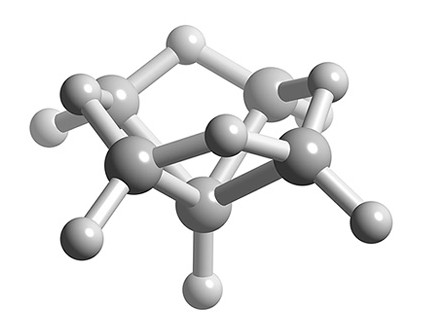
Ball and stick representation of the structure of B5H9.
What is the structure of B6H62-?
- Total number of valence electrons = (6 x B) + (3 x H) = (6 x 3) + (6 x 1) + 2 = 26
- Number of electrons for each B-H unit = (6 x 2) = 12
- Number of skeletal electrons = 26 – 12 = 14
- Number SEP = 14/2 = 7
- If n+1 = 7 and n boron atoms, then n = 6
- Structure of n = 6 is octahedral, therefore B6H62- is a closo structure based upon an octahedral structure.
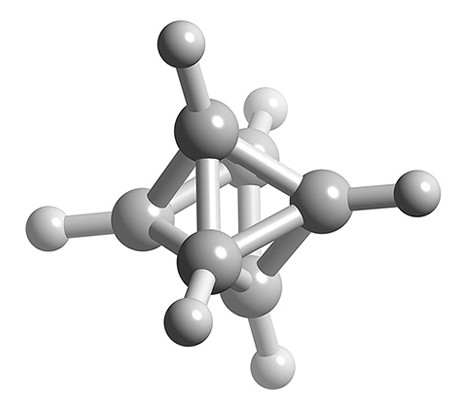
Ball and stick representation of the structure of B6H62-.
Table \(\PageIndex{1}\) provides a summary of borane cluster with the general formula BnHnx- and their structures as defined by Wade’s rules.
| Type | Basic formula | Example | # of verticies | # of vacancies | # of e- in B + charge | # of bonding MOs |
|---|---|---|---|---|---|---|
| Closo | BnHn2- | B6H62- | n | 0 | 3n + 2 | n + 1 |
| Nido | BnHn4- | B5H9 | n + 1 | 1 | 3n + 4 | n + 2 |
| Arachno | BnHn6- | B4H10 | n + 2 | 2 | 3n + 6 | n + 3 |
| Hypho | BnHn8- | B5H112- | n + 3 | 3 | 3n + 8 | n + 4 |
Bibliography
- R. W. Rudolph, Acc. Chem. Res., 1976, 9, 446.
- K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1.

