6.3C: Solid Metallic Elements

A metal (from Greek μέταλλον métallon, "mine, quarry, metal") is a material (an element, compound, or alloy) that is typically hard, opaque, shiny, and has good electrical and thermal conductivity. Metals are generally malleable - that is, they can be hammered or pressed permanently out of shape without breaking or cracking - as well as fusible (able to be fused or melted) and ductile (able to be drawn out into a thin wire). About 91 of the 118 elements in the periodic table are metals (some elements appear in both metallic and non-metallic forms).

Atoms of metals readily lose their outer shell electrons, resulting in a free flowing cloud of electrons within their otherwise solid arrangement. This provides the ability of metallic substances to easily transmit heat and electricity. While this flow of electrons occurs, the solid characteristic of the metal is produced by electrostatic interactions between each atom and the electron cloud. This type of bond is called a metallic bond.

Cubic and hexagonal close packing.

Crystalline solids consist of repeating patterns of its components in three dimensions (a crystal lattice) and can be represented by drawing the structure of the smallest identical units that, when stacked together, form the crystal. This basic repeating unit is called a unit cell.

Many metals adopt close packed structures i.e. cubic close packed (face centred cubic) and hexagonal close packed structures. A simple model for both of these is to assume that the metal atoms are spherical and are packed together in the most efficient way (close packing or closest packing). For closest packing, every atom has 12 equidistant nearest neighbours, and therefore a coordination number of 12. If the close packed structures are considered as being built of layers of spheres then the difference between hexagonal close packing and cubic close packed is how each layer is positioned relative to others. It can be envisaged that for a regular buildup of layers:

• hexagonal close packing has alternate layers positioned directly above/below each other, A,B,A,B,...
• cubic close packed (face centered cubic) has every third layer directly above/below each other, A,B,C,A,B,C,...

Body centred cubic

This is not a close packed structure. Here each metal atom is at the centre of a cube with 8 nearest neighbors, however the 6 atoms at the centres of the adjacent cubes are only approximately 15% further away so the coordination number can therefore be considered to be 14 when these are included. Note that if the body centered cubic unit cell is compressed along one 4 fold axis the structure becomes cubic close packed (face centred cubic).

Cubic, Hexagonal and Body-centred Packing

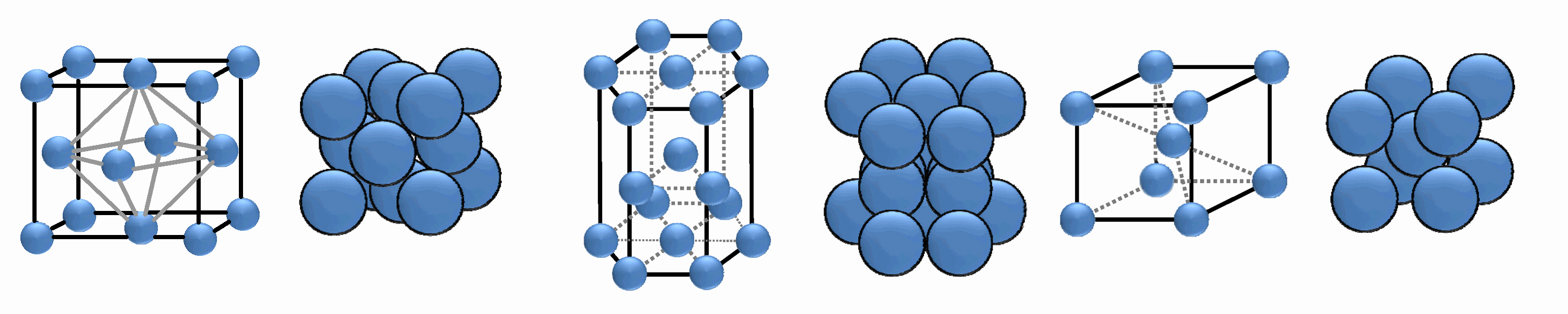
cubic close packing (ccp) packing efficiency =74% CN=12

hexagonal close packing (hcp) packing efficiency =74% CN=12

body-centred cubic packing (bcc) packing efficiency =68% CN=8

Trends in melting point

Melting points are chosen as a simple measure of the stability or strength of the metallic lattice. Some simple trends can be noted. The transition metals have generally higher melting points than the others. In the alkali metals (Group 1) and alkaline earth metals (Group 2) the melting point decreases as atomic number increases, but in transition metal groups with incomplete d-orbital subshells, the heavier elements have higher melting points. For a given period, the melting points reach a maximum at around Group 6 and then fall with increasing atomic number.

Mercury, caesium and gallium have melting points below 30 °C whereas all the other metals have sufficiently high melting points to be solids at "room temperature". The structures of the metals can be summarised by the table below which shows that most metals crystallise in roughly equal amounts of bcc, hcp and ccp lattices.

Crystal structure of metallic elements in the periodic table
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
H																	He
453.69 Li bcc	1560 Be hcp					MP (K) At. Symbol Lattice type						B	C	N	O	F	Ne
370.87 Na bcc	923 Mg hcp											933.47 Al ccp	Si	P	S	Cl	Ar
336.53 K bcc	1115 Ca ccp	1814 Sc hcp	1941 Ti hcp	2183 V bcc	2180 Cr bcc	1519 Mn	1811 Fe bcc	1768 Co hcp	1728 Ni ccp	1357.8 Cu ccp	692.68 Zn hcp	302.91 Ga	Ge	As	Se	Br	Kr
312.46 Rb bcc	1050 Sr ccp	1799 Y hcp	2128 Zr hcp	2750 Nb bcc	2896 Mo bcc	2430 Tc hcp	2607 Ru hcp	2237 Rh ccp	1828 Pd ccp	1235 Ag ccp	594 Cd	430 In	505 Sn	904 Sb	Te	I	Xe
301.59 Cs bcc	1000 Ba bcc		2506 Hf hcp	3290 Ta bcc	3695 W bcc	3459 Re hcp	3306 Os hcp	2719 Ir ccp	2041.4 Pt ccp	1337.33 Au ccp	234.32 Hg	577 Tl hcp	600.61 Pb ccp	544.7 Bi	527 Po	At	Rn

Group 1: Alkali metals

The alkali metals have their outermost electron in an s-orbital and this electronic configuration results in their characteristic properties. The alkali metals provide the best example of group trends in properties in the periodic table, with elements exhibiting well-characterized homologous behaviour.

The alkali metals have very similar properties: they are all shiny, soft, highly reactive metals at standard temperature and pressure and readily lose their outermost electron to form cations with charge +1. They can all be cut easily with a knife due to their softness, exposing a shiny surface that tarnishes rapidly in air due to oxidation by atmospheric moisture and oxygen. Because of their high reactivity, they must be stored under oil to prevent reaction with air, and are found naturally only in salts and never as the free element. In the modern IUPAC nomenclature, the alkali metals comprise the group 1 elements, excluding hydrogen (H), which is only nominally considered a group 1 element.

Group 2: Alkali Earth Metals

extended structures of Li, Mg, Ca

Lithium -bcc

Magnesium -hcp Spacefill UnitCell All Layers A B A B A layers

Calcium -ccp Spacefill UnitCell All Layers A B C A B C layers

Note that Housecroft and Sharpe has Ca and Sr both listed as hexagonal and not cubic (face) close packed lattices. Calcium and Strontium exist in several allotropic forms and the lowest temperature forms (for Ca < 450 °C) are ccp. At high temperatures phase transitions occur to give hexagonal.

Return to the course outline or move on to Lecture 5: Structure of the elements Boron, Carbon and Phosphorus, Sulfur.

References

Much of the information in these course notes has been sourced from Wikipedia under the Creative Commons License.
'Inorganic Chemistry' - C. Housecroft and A.G. Sharpe, Prentice Hall, 4th Ed., 2012, ISBN13: 978-0273742753, pps 24-27, 43-50, 172-176, 552-558, 299-301, 207-212
'Basic Inorganic Chemistry' - F.A. Cotton, G. Wilkinson and P.L. Gaus, John Wiley and Sons, Inc. 3rd Ed., 1994.
'Introduction to Modern Inorganic Chemistry' - K.M. Mackay, R.A. Mackay and W. Henderson, International Textbook Company, 5th Ed., 1996.