3.4: Point Groups
- Page ID
- 2572
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Point groups are used to describe molecular symmetries and are a condensed representation of the symmetry elements a molecule may posses. This includes both bond and orbital symmetry. Knowing molecular symmetry allows for a greater understanding of molecular structure and can help to predict many molecular properties.
Introduction
Point groups are a quick and easy way to gain knowledge of a molecule. They not only contain a molecule's symmetry elements, but also give rise to a character table, which is a complete set of irreducible representations for a point group. A molecule's point group can be determined by either elucidating each symmetry element contained in a molecule or by properly using the Schreiber chart (see below).
Point groups usually consist of (but are not limited to) the following elements:
- E - The identity operator. This operation leaves a molecule completely unchanged and exists for mathematical purposes.
- Cn - The Cn proper axis of rotation is a 360/n° rotation that when performed leaves a molecule the same. A proper rotation with the highest value of n is known as the major axis of rotation.
- σ - The mirror plane. The mirror plane can be described as a plane which produces a reflection of part of a molecule that is unnoticeable and can be labeled as either σh , σv , σd.
- i - The inversion center. A molecule has a center of inversion if, when inverted, the molecule is unchanged.
See the section on symmetry elements for a more thorough explanation of each.
Each point group is associated with a specific combination of symmetry elements
Each point group has it's own combination of symmetry elements. Listed below are some of the many point groups and their respective symmetry elements, according to category, followed by a representative example.
Non axial groups
C1: E C1: E, i
Cn groups
C2: E, C2 (notice the major axis of rotation is the point group) C3: E, C3, C32
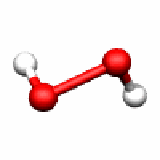
H2O2 C2
Dn groups
D2: E C2(z), C2(y), C2(x) D3: E, 2C3, 3C2
Cnv groups
C2v: E, C2, σv(xz), σv'(yz) C3v: E, 2C3, 3σv
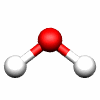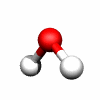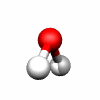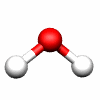
H2O C2v
Cnh groups
C2h: E, C2, i, σh C3h: E, C3, C32, σh, S3, S33
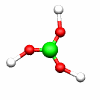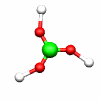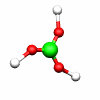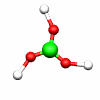
B(OH)3
Dnh groups
D2h: E
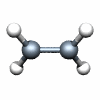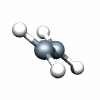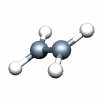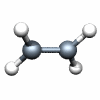
C2H4 D2h
How to determine a molecules point group
A molecule's point group can be determined by calculating all the symmetry elements of a molecule and matching them to a respective point group. This process, however, is greatly simplified when the Schreiber chart is used:
References
- Housecroft, Catherine E.; Sharpe, Alan G., Inorganic Chemistry, 3rd Ed. Pearson Education Limited 2008, Chapter 4
- Koster, George F.; Wheeler, Robert G.; Dimmock, John O., The Properties of Thirty-Two Point Groups, The MIT Press 1963
- Bertolucci, Michael D.; Harris, Daniel C., Symmetry and Spectroscopy: An Introduction to Vibrational and Electronic Spectroscopy, Dover Publications 1989
Outside Links
Problems
- Determine the point group of BH3 by calculating all it's symmetry elements then use the chart and determine which method is faster.
- Determine the point groups of BH3 and NH3. Why is there a difference?
- What is the point group of PPh3?
- Determine the point groups of CO2 and H2O and then compare them.
- Propose a molecule with no symmetry. What is it's point group?

