10.2: Metal-Insulator Transitions
- Page ID
- 183353
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Chapter 6 we learned that metals and insulators not only have different electrical properties but also have very different crystal structures. Metals tend to have high coordination numbers (typically 8 or 12) whereas insulators have low coordination numbers that can be rationalized as "octet" bonding arrangements. For example, in crystalline Si or Ge (diamond structure), each atom has four nearest neighbors. There are two electrons per bond, and thus each atom has eight electrons in its valence shell. Sn, the element below Ge, exists in two different forms, one (gray tin) with the diamond structure that is a brittle narrow-gap semiconductor, and the other (white tin) with a body-centered tetragonal structure that is a malleable metal. These two forms are very close in energy, and in fact metallic white tin transforms to the brittle semiconducting gray form at low temperature. Extremely cold weather in 18th century Europe caused many tin organ pipes to break and eventually turn to dust. This transformation has been called tin blight, tin disease, tin pest or tin leprosy. The dust is actually grey tin, which lacks the malleability of its metallic cousin white tin.
Under experimentally accessible temperatures and pressures, Si and Ge are always semiconducting (i.e., insulating), and Pb is always metallic. Why is Sn different? The reason has to do with orbital overlap. Theory tells us in fact that any (and all) insulators should become metallic at high enough pressure, or more to the point, at high enough density. For most insulators, however, the pressures required are far beyond those that we can achieve in the laboratory.

How can we rationalize the transition of insulators to the metallic state? Indeed, how can we understand the existence of insulators at all?
The Hubbard Model
Let's consider a chain of a large number (N) of atoms as we did in Chapter 6. For convenience, we can say that these are atoms such as H, Na, or Cs that have one valence electron. The simple band model we developed earlier suggests that the chain should be metallic, because N atoms combine to make N orbitals, and the N valence electrons only fill the band of orbitals halfway. But this conclusion doesn't depend on the density, which creates a paradox. If atoms in the chain are very far apart, we suspect that the electrons should localize on the atoms.
|
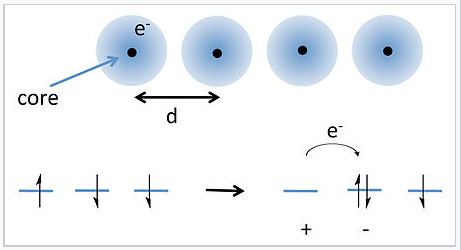
Electron hopping in a 1-D chain of atoms. |
A solution to this problem was proposed by J. Hubbard in 1963.[1] Hubbard considered the energy required to transfer an electron from an atom to its nearest neighbor, as shown in the picture at the right. Because each atom already has one electron (with random spin), moving an electron over by one atom requires overcoming the energy of electron-electron repulsion to make a cation-anion pair. For well-separated atoms this energy (U) is given by:
\[U = IP -Ea -\frac{e^{2}}{4\pi \varepsilon_{0} d}\]
where IP and EA are the ionization energy and electron affinity, ε0 is the permittivity of free space, and the last term in the equation represents the coulombic attraction between the cation and the anion. For atoms such as alkali metals, U is on the order of 3–5 eV, which is much larger than the thermal energy kT. Thus we expect there to be very few anion-cation pairs at room temperature, and the chain of atoms should be insulating.
|
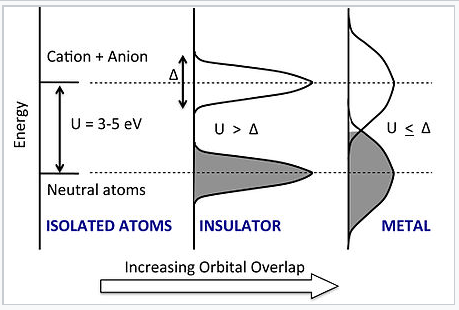
Energy vs. DOS for the chain of atoms as the density and degree of orbital overlap between atoms increases. Increasing overlap broadens the neutral atom and anion-cation states into bands, each of which has a bandwidth Δ. A transition to the metallic state occurs abruptly when Δ exceeds the Hubbard gap U. |
What happens when we squeeze the atoms together? In the Hubbard model, as the distance between atoms decreases, the energies of both the neutral atom states and the anion-cation states broaden into bands, each of which has a band width Δ. The lower band can accommodate exactly N electrons (not 2N as in the MO picture we developed earlier) because each orbital can only take one electron without spin-pairing. Thus for small Δ the lower band is full and the upper band is empty. However, as we continue to compress the chain, the orbital overlap becomes so strong that Δ ≈ U. At this point, the bands overlap and some of the electrons fill the anion-cation states. The chain then becomes conducting and the material is metallic.
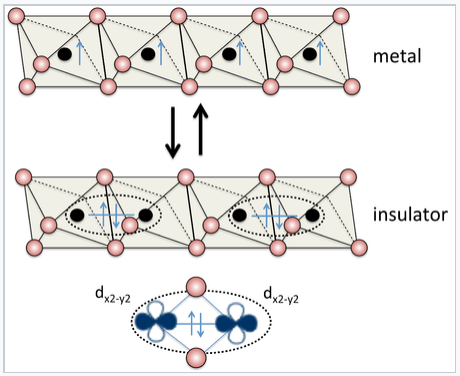
Some materials, such as Sn and VO2, happen to have just the right degree of orbital overlap to make the Hubbard transition occur by changing the temperature or pressure. Such materials can be very useful for electrical switching, as illustrated at the right for rutile structure VO2. Most materials are far away from the transition, either on the metallic or insulating side. An interesting periodic trend that illustrates this concept can be seen among the transition metal monoxides, MO (M = Ti, V, Cr, Mn, Fe, Co, Ni), all of which have the NaCl structure. TiO and VO are metallic, because the 3d orbitals have significant overlap in the structure. However, CrO, MnO, FeO, CoO, and NiO are all insulators, because the 3d orbitals contract (and therefore Δ < U) going across the transition metal series. In contrast, the analogous sulfides (TiS, VS,....NiS) are all metallic. The sulfides have the NiAs structure, in which all the metal atoms are eclipsed along the stacking axis (the hexagonal c-axis). The short metal-metal distances along that axis result in strong orbital overlap, making Δ > U.
|
Vanadium dioxide has the rutile structure, and in its undistorted form it is metallic, with one valence electron per V atom. Distortion of the lattice makes pairs of V atoms, resulting in an electronically insulating state. The metal-insulator transition can be driven reversibly by changing the temperature, pressure, or orbital occupancy. Electrical switching of this transition in VO2 is being studied for applications in high performance thin film transistors[2] |
The Mott Model
A simpler, less atomistic model of the metal-insulator transition was formulated by Neville Mott.[3] The Mott model considers the behavior of an electron in a material as a function of the density of all the other valence electrons. We know for a one-electron hydrogen-like atom (H, Na, Cs, etc.) the Schrödinger equation contains a potential energy term:
\[V(r) = -(\frac{e^{2}}{4 \pi \varepsilon_{0} r})\]
This potential energy function gives rise to familiar ladder of allowed energy levels in the hydrogen atom. However, in a metal, this Coulomb potential must be modified to include the screening of nuclear charge by the other electrons in the solid. In this case there is a screened Coulomb potential:
\[V(r) = -(\frac{e^{2}}{4 \pi \varepsilon_{0}r}) exp(-qr)\]
where q, which is the inverse of the screening length, is given by:
\[ q^{2} = 4m_{e}^{2}(\frac{3n}{\pi})^{\frac{1}{3}}(\frac{2\pi}{h})\]
Here n is the density of atoms (or valence electrons), me is the electron mass, and h is Planck's constant. At distances much larger than the screening length q-1, the electron no longer "feels" the charge on the nucleus. Mott showed that there is a critical density of electrons nc above which the valence electrons are no longer bound by individual nuclei and are free to roam the crystal. This critical density marks the transition to the metallic state, and is given by the Mott criterion:
\[\mathbf{n_{c}^{\frac{1}{3}}a_{H} \approx 0.26}\]
In this equation, aH is an effective Bohr radius for the valence electrons in the low-density limit, e.g. the average orbital radius of electrons in the 6s shell of a Cs atom when computing the value for Cs metal.
|
Solutions of lithium metal in liquid ammonia at low (top, ionic conductor) and higher (bottom, metal) Li concentration. From a video by Joshua Judkins |
The important concept from the Mott model is that the metal-insulator transition depends very strongly on the density of valence electrons. This is consistent with the orbital overlap model of Hubbard, but also more general in the sense that it does not depend on a periodic structure of atoms. The Mott model is thus applicable to such diverse systems as metal atoms dissolved in liquid ammonia, metal atoms trapped in frozen gas matrices, and dopants in semiconductors.[4] In some systems, it is possible to continuously tune the density of valence electrons with rather striking results. For example, dissolving alkali metal (Li, Na, ...) in liquid ammonia (bp -33 oC) produces a blue liquid. The solvated alkali cations and negatively charged electrons impart ionic conductivity (as in a salt solution) but not electronic conductivity to the blue liquid ammonia solution. But as the concentration of electrons increases, a reflective, bronze-colored liquid phase forms that floats over the blue phase. This bronze phase is metallic and highly conducting. Eventually, with enough alkali metal added, the entire liquid is converted to the electronically conducting bronze phase.
The electrical switching of VO2 between insulating and metallic phases (see above) can also be rationalized in terms of the Mott transition. Adding more electron density (by chemical or electric field doping) increases the concentration of valence electrons, driving the phase transition to the metallic state.
Thermodynamics and phase transitions
Thermodynamically, the metal-insulator transition is a first-order phase transition. In such a transition, the structure and properties change abruptly (think of the breakfast-to-lunch transition at McDonalds - there is just no way to get pancakes after, or hamburgers before 10:30 AM![5]). Thus in the case of Sn metal, the changes in structure (from four- to eight-coordination) and in electronic conductivity (insulator to metal) occur simultaneously. As in other first order phase transitions such as ice to water to steam, there is a latent heat associated with the transition and a discontinuity in derivative properties such as the heat capacity.
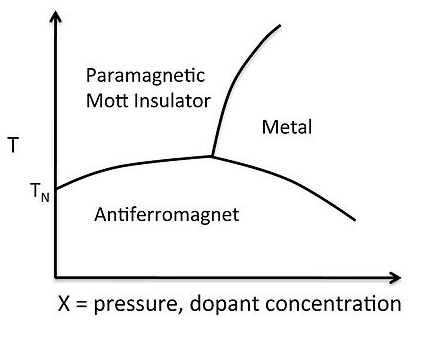
A typical phase diagram for a metal-insulator transition is shown at the right for V2O3. The octahedrally coordinated V3+ ion has a d2 electron count, so there are two unpaired spins per atom, and at low temperature the spins in the lattice order antiferromagnetically. As we learned in Chapter 8, above the Néel temperature an antiferromagnet becomes a paramagnet, which is also a Mott insulator. Increasing the pressure, or doping with electrons (e.g., by substituting some d3 Cr3+ for V3+) pushes the electron density over the Mott transition, the spins pair, and the solid becomes metallic.