8.2: Close-packing and Interstitial Sites
- Page ID
- 183339
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Many common inorganic crystals have structures that are related to cubic close packed (face-centered cubic) or hexagonal close packed sphere packings. These packing lattices contain two types of sites or "holes" that the interstitial atoms fill, and the coordination geometry of these sites is either tetrahedral or octahedral. An interstitial atom filling a tetrahedral hole is coordinated to four packing atoms, and an atom filling an octahedral hole is coordinated to six packing atoms. In both the hexagonal close packed and cubic close packed lattices, there is one octahedral hole and two tetrahedral holes per packing atom.
Question: Would anions or cations be better as packing atoms?
We might expect that anions, which are often larger than cations, would be better suited to the positions of packing atoms. While this is often true, there are many examples of structures in which cations are the packing atoms, and others in which the distinction is arbitrary. The NaCl structure is a good example of the latter.
|
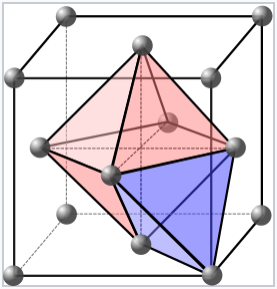
One octahedral and one tetrahedral site in a face-centered cubic unit cell. Each cell contains four packing atoms (gray), four octahedral sites (pink), and eight tetrahedral sites (blue). |
In the NaCl structure, shown on the right, the green spheres are the Cl- ions and the gray spheres are the Na+ ions. The octahedral holes in a face-centered cubic lattice can be found at fractional coordinates (1/2 1/2 1/2), (1/2 0 0), (0 1/2 0), and (0 0 1/2). There are four of these holes per cell, and they are filled by the chloride ions. The packing atoms (Na+) have coordinates (0 0 0), (0 1/2 1/2), (1/2 1/2 0), and (1/2 0 1/2). Note that each of the Na+ positions is related to a Cl- position by a translation of (1/2 0 0). Another way of stating this is that the structure consists of two interpenetrating fcc lattices, which are related to each other by a translation of half the unit cell along any of the three Cartesian axes. We could have equivalently placed the Cl ions at the fcc lattice points and the Na ions in the octahedral holes by simply translating the origin of the unit cell by (1/2 0 0). Thus the distinction between packing and interstitial atoms in this case is arbitrary.
|
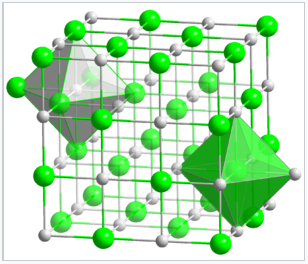
Crystal structure of NaCl. Both the Na+ and Cl- ions are octahedrally coordinated. |
NaCl is interesting in that it is a three-dimensional checkerboard, and thus there are no NaCl "molecules" that exist in the structure. When this structure was originally solved (in 1913 by using X-ray diffraction) by W. L. Bragg, his interpretation met resistance by chemists who thought that precise integer stoichiometries were a consequence of the valency of atoms in molecules. The German chemist P. Pfeiffer noted in 1915 that ‘the ordinary notion of valency didn’t seem to apply’, and fourteen years later, the influential chemist H. E. Armstrong still found Bragg’s proposed structure of sodium chloride ‘more than repugnant to the common sense, not chemical cricket’! Nevertheless, Bragg and his father, W. H. Bragg, persevered and used the then-new technique of X-ray diffraction to determine the structures of a number of other compounds, including diamond, zincblende, calcium fluoride, and other alkali halides. These experiments gave chemists their first real look at the atomic structure of solids, and laid the groundwork for X-ray diffraction experiments that later elucidated the structures of DNA, proteins, and many other compounds. For their work on X-ray diffraction the Braggs received the Nobel prize in Physics in 1915.
|
The lattice dimensions and positions of atoms in crystals such as NaCl are inferred from diffraction patterns. |
Since each type of atom in the NaCl structure forms a face-centered cubic lattice, there are four Na and four Cl atoms per NaCl unit cell. It is because of this ratio that NaCl has a 1:1 stoichiometry. The shaded green and gray bipyramidal structures in the NaCl lattice show that the Na+ ions are coordinated to six Cl- ions, and vice versa. The NaCl structure can be alternatively drawn as a stacking of close-packed layer planes, AcBaCbAcBa... along the body diagonal of the unit cell. Here the uppercase letters represent the packing atoms, and the lower case letters are the interstitial atoms. This layered packing is illustrated below:
NaCl structure
- ------------ A
- - - -c- - - -
- ------------ B
- - - -a- - - -
- ------------ C
- - - -b- - - -
- ------------ A
- - - -c- - - -
- ------------ B
- - - -a- - - -
- ------------ C
- - - -b- - - -
- ------------ A
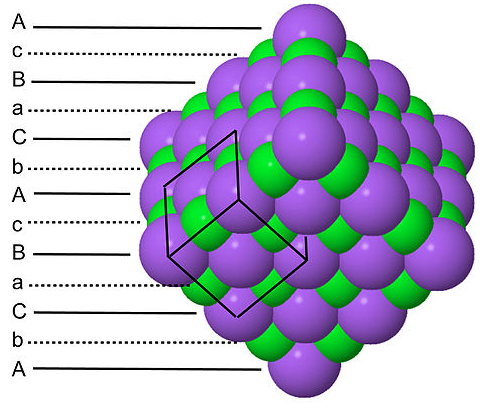
Note that both the packing atoms and interstitials are stacked in the sequence A-B-C-A-B-C..., in keeping with the fact that each forms a cubic close-packed lattice.
The NaCl structure is fairly common among ionic compounds:
- Alkali Halides (except CsCl, CsBr, and CsI)
- Transition Metal Monoxides (TiO, VO,..., NiO)
- Alkali Earth Oxides and Sulfides (MgO, CaO, BaS... except BeO and MgTe)
- Carbides and Nitrides (TiC, TiN, ZrC, NbC) -these are very stable refractory, interstitial alloys (metallic)
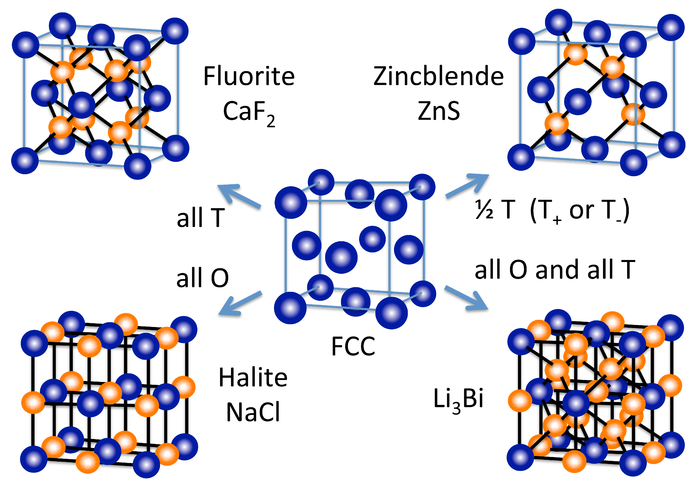
A number of other inorganic crystal structures are formed (at least conceptually) by filling octahedral and/or tetrahedral holes in close-packed lattices. The figure at the right shows some of the most common structures (fluorite, halite, zincblende) as well as a rather rare one (Li3Bi) that derive from the fcc lattice. From the hcp lattice, we can make the NiAs and wurzite structures, which are the hexagonal relatives of NaCl and zincblende, respectively.
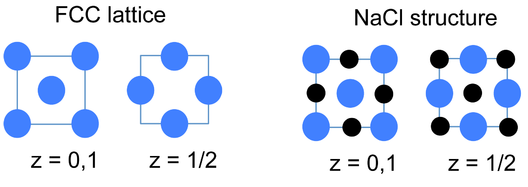
An alternative and very convenient way to represent inorganic crystal structures (especially complex structures such as Li3Bi) is to draw the unit cell in slices along one of the unit cell axes. This kind of representation is shown at the left for the fcc lattice and the NaCl structure. Since all atoms in these structures have z-coordinates of either 0 or 1/2, only those sections need to be drawn in order to describe the contents of the unit cell. It is a useful exercise to draw some of the fcc compound structures (above) in sections.