5.12: Ligand Substitution Reactions
- Page ID
- 188714
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transition metal complexes can exchange one ligand for another, and these reactions are important in their synthesis, stereochemistry, and catalytic chemistry. The mechanisms of chemical reactions are intimately connected to reaction kinetics. As in organic chemistry, the mechanisms of transition metal reactions are typically inferred from experiments that examine the concentration dependence of the incoming and outgoing ligands on the reaction rate, the detection of intermediates, and the stereochemistry of the reactants and products.
Thermodynamic vs. kinetics. When we think about the reactions of transition metal complexes, it is important to recall the distinction between their thermodynamics and kinetics. Take for example the formation of the square planar tetracyanonickelate complex:
\[\ce{Ni^{2+}_{(aq)} + 4CN^{-}_{(aq)} = [Ni(CN)4]^{2-}_{(aq)}} \: \: \: K_{(eq)} \approx 10^{30} M^{-4}\]
Thermodynamically, [Ni(CN)4]2- is very stable, meaning that the equilibrium above lies very far to the right. Kinetically, however, the complex is labile, meaning that it can exchange its ligands rapidly. For example the exchange between a 13C labeled CN- ion and a bound CN- ligand occurs on the timescale of tens of milliseconds:
\[\ce{[Ni(CN)4]^{2-}_{(aq)} + *CN^{-}_{(aq)} -> [Ni(CN)3(*CN)]^{2-} + CN^{-}_{(aq)}} \: \: k_{exchange} \approx 10^{2}M^{-1}s^{-1}\]
Conversely, a compound can be thermodynamically unstable but kinetically inert, meaning that it takes a relatively long time to react. For example, the [Co(NH3)6]3+ ion is unstable in acid, but its hydrolysis reaction with concentrated HCl takes about one week to go to completion at room temperature:
\[\ce{[Co(NH3)6]^{3+}_{(aq)} + 6H3O^{+}_{(aq)} -> [Co(H2O)6]^{3+}_{(aq)} + 6NH4^{+}_{(aq)}} \: \: K_{eq} \approx 10^{30}\]
Henry Taube, who studied the mechanisms of ligand exchange reactions in simple test tube experiments, classified transition metal complexes as labile if their reaction half-life was one minute or less, and inert if they took longer to react. The dynamic range of ligand substitution rates is enormous, spanning at least 15 orders of magnitude. On the timescale of most laboratory experiments, the Taube definition of lability is a useful one for classifying reactions into those that have low and high activation energies. As we will see, the crystal field stabilization energy (CFSE) plays a key role in determining the activation energy and therefore the rate of ligand substitution.
|
Henry Taube (Stanford University) received the 1983 Nobel Prize for his work on the electron transfer and ligand exchange reactions of transition metal complexes |
Crystal field stabilization energy and ligand exchange rates. Let's consider a very commmon and simple ligand exchange reaction, which is the substitution of one water molecule for another in an octahedral [M(H2O)6]n+ complex. Since the products (except for the label) are the same as the reactants, we know that ΔG° = 0 and Keq = 1 for this reaction. The progress of the reaction can be monitored by NMR by using isotopically labeled water (typically containing 17O or 18O):
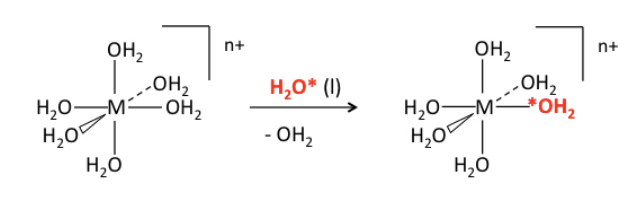
The most striking thing about this (otherwise boring) reaction is the vast difference in rate constants - about 14 orders of magnitude - for different metal ions and oxidation states:
| Mn+ | log k (sec-1) |
|---|---|
| Cr3+ |
|
| V2+ |
|
| Cr2+ |
|
| Cu2+ |
|

While at first it may seem strange that the same ion in two different oxidation states (Cr3+ vs. Cr2+) would be inert or labile, respectively, we can begin to rationalize the difference by drawing d-orbital splitting diagrams for the complexes. What we find is that octahedral complexes that have high CFSE (Cr3+, V2+) tend to be inert. Conversely, ions with electrons in high energy eg orbitals (Cr2+, Cu2+) tend to be labile. In the case of Cr3+ and V2+, the energy penalty for distorting the complex away from octahedral symmetry - to make, for example, a 5- or 7-coordinate intermediate - is particularly high. This activation energy for ligand substitution is lower for Cr2+ and Cu2+, which already have electrons in antibonding eg orbitals.
Based on the rules we developed for calculating the CFSE of transition metal complexes, we can now predict the trends in ligand substitution rates:
- Octahedral complexes with d3 and d6(low spin) configurations, such as Cr3+ (d3), Co3+ (d6), Rh3+ (d6), Ru2+ (d6), and Os2+ (d6) tend to be substitution-inert because of their high CFSE.
- Square planar d8 complexes, especially those in the 4d and 5d series, are also substitution-inert. Examples are complexes of Pd2+, Pt2+, and Au3+.
- Intermediate cases are complexes of Fe3+, V3+, V2+, Ni2+, and of main group ions (Be2+, Al3+) that are hard Lewis acids. These complexes make strong metal-oxygen bonds and have water exchange rates in the range of 101-106 s-1.
- Ions with zero CFSE exchange water molecules on a timescale of nanoseconds (k ≈ 108-109 s-1). These include ions with d0, d5 (high spin), and d10 electron counts, including alkali metal (Li+, Na+, K+, Rb+, Cs+) and alkali earth (Mg2+, Ca2+, Sr2+, Ba2+) cations, Zn2+, Cd2+, Hg2+, and Mn2+. In these cases the CFSE is zero and the energetic cost of breaking octahedral symmetry is relatively low.
- For p-block elements, faster exchange occurs with larger ions (e.g., Ba2+ > Ca2+ and Ga3+ > Al3+), because Lewis acid strength decreases with increasing ion size.
- The Cu2+ ion (d9), as a Jahn-Teller ion, is already distorted away from octahedral symmetry and is therefore quite labile, exchanging water ligands at a rate of about 108 s-1.
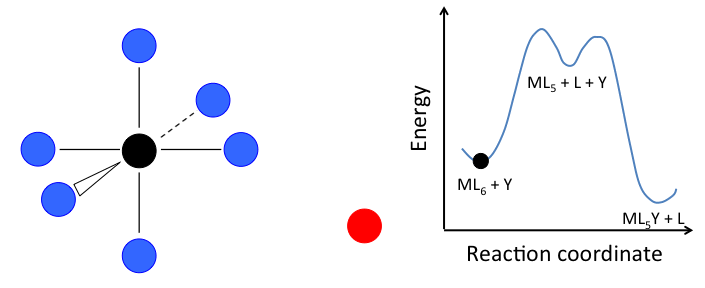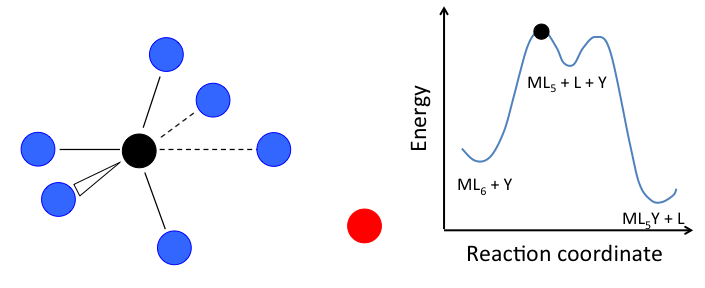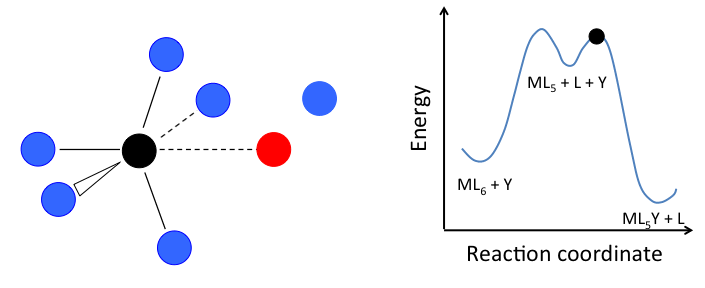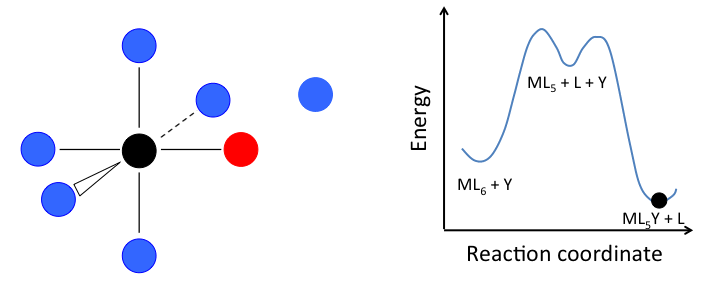
Ligand Substitution Mechanisms. For an MLn complex undergoing ligand substitution, there are essentially three different reaction mechanisms:
- In the dissociative mechanism, a MLn complex first loses a ligand to form an MLn-1 intermediate, and the incoming ligand Y reacts with the MLn-1 fragment:
\[\ce{L_{n-1}M-L <=>[-L, k_{1}][+L, k_{-1}] L_{n-1}M-\Box ->[+Y, k_{2}] L_{n-1}M-Y}\]
This mechanism is illustrated below for ligand substitution on an octahedral ML6 complex. The intermediate state in this example involves a trigonal bipyramidal ML5 fragment as well as free L and Y ligands.
If the rate determining step is the dissociation of L from the complex, then the concentration of Y does not affect the rate of reaction, leading to the first-order rate law:
\[Rate=k_{1}[ML_{n}]\]
In the case of an octahedral complex, this reaction would be first order in ML6 and zero order in Y, but only if the highest energy transition state is the one that precedes the formation of the ML5 intermediate. If the two transition states are close in energy (as in the case of the animation at the right), then the rate law becomes more complicated. In this case, we can simplify the problem by assuming a low steady-state concentration of the MLn intermediate. The resulting rate law is:
\[Rate= \frac{k_{1}k_{2}[Y][ML_{n}]}{k_{-1}[L] + k_{2}[Y]}\]
which reduces to the simpler first-order rate law when k2[Y] >> k-1[L]. Because the formation of the transition state involves dissociation of a ligand, the entropy of activation is always positive in the dissociative mechanism.
- In the associative mechanism, the incoming ligand Y attacks the MLn complex, transiently forming an MLnY intermediate, and the intermediate then loses a ligand L forming the MLn-1Y product
Complexes that undergo associative substitution are typically either coordinatively unsaturated or contain a ligand that can change its bonding to the metal, e.g. a change in the hapticity or bending of a nitric oxide ligand (NO). In homogeneous catalysis, the associative pathway is desirable because the binding event, and hence the selectivity of the reaction, depends not only on the nature of the metal catalyst but also on the molecule that is involved in the catalytic cycle.
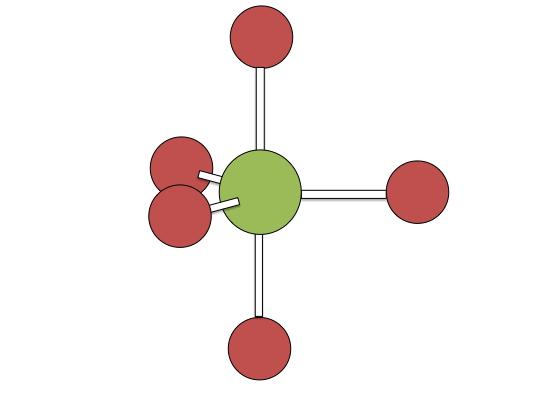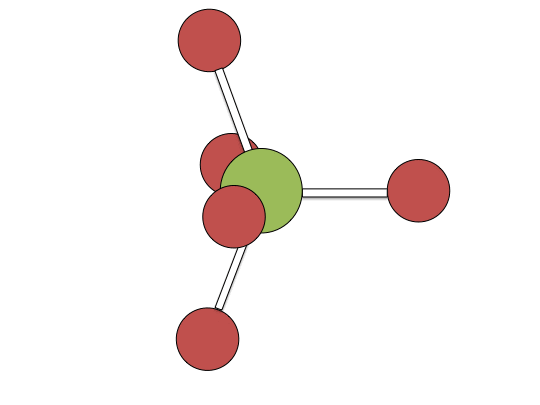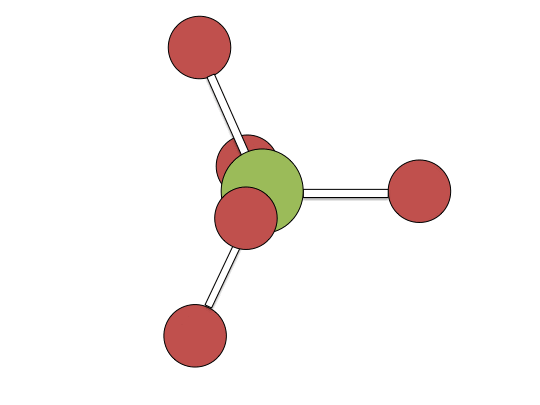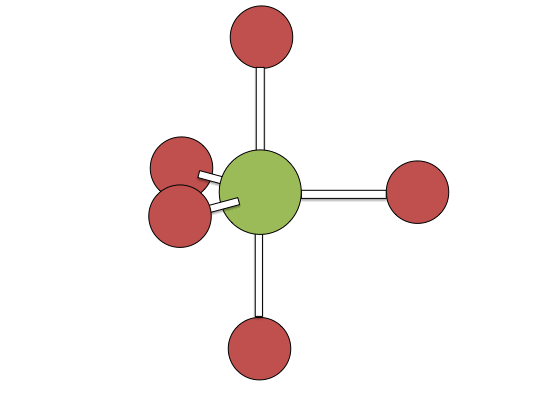
Berry pseudorotation mechanism
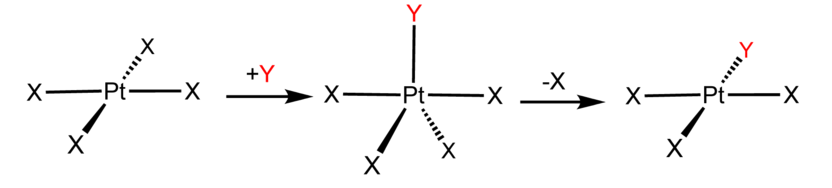
Examples of associative mechanisms are commonly found in the chemistry of d8 square planar metal complexes, e.g. Vaska's complex (IrCl(CO)[P(C6H5)3]2) and tetrachloroplatinate(II). These compounds (ML4) bind the incoming (substituting) ligand Y to form pentacoordinate intermediates ML4Y, which in a subsequent step dissociate one of their ligands. Although the incoming ligand is initially bound at an equatorial site, the Berry pseudorotation provides a low energy pathway for all ligands to sample both the equatorial and axial sites. Ligand dissociation must occur from an equatorial site according to the principle of microscopic reversibility. Dissociation of Y results in no reaction, but dissociation of L results in net substitution, yielding the d8 complex ML3Y. The first step is typically rate determining. Thus, the entropy of activation is negative, which indicates an increase in order in the transition state. Associative reactions follow second order kinetics: the rate of the appearance of product depends on the concentration of both ML4 and Y.
The Trans Effect, which is connected with the associative mechanism, controls the stereochemistry of certain ligand substitution reactions.
The trans effect refers to the labilization (making more reactive) of ligands that are trans to certain other ligands, the latter being referred to as trans-directing ligands. The labilization of trans ligands is attributed to electronic effects and is most notable in square planar complexes, but it can also be observed with octahedral complexes.[18] The cis effect is most often observed in octahedral complexes.
In addition to the kinetic trans effect, trans ligands also have an influence on the ground state of the molecule, the most notable ones being bond lengths and stability. Some authors prefer the term trans influence to distinguish this from the kinetic effect,[19] while others use more specific terms such as structural trans effect or thermodynamic trans effect.[18]
The discovery of the trans effect is attributed to Ilya Ilich Chernyaev,[20] who recognized it and gave it a name in 1926.[21]
The intensity of the trans effect (as measured by the increase in the rate of substitution of the trans ligand) follows this sequence:
- F−, H2O, OH− < NH3 < py < Cl− < Br− < I−, SCN−, NO2−, SC(NH2)2, Ph− < SO32− < PR3, AsR3, SR2, CH3− < H−, NO, CO, CN−, C2H4
Note that weak field ligands tend to be poor trans-directing ligands, whereas strong field ligands are strongly trans-directing.
The classic example of the trans effect is the synthesis of cisplatin and its trans isomer.[22] Starting from PtCl42−, the first NH3 ligand is added to any of the four equivalent positions at random. However, since Cl− has a greater trans effect than NH3, the second NH3 is added trans to a Cl− and therefore cis to the first NH3.

If, on the other hand, one starts from Pt(NH3)42+, the trans product is obtained instead:

The trans effect in square complexes can be explained in terms of the associative mechanism, described above, which goes through a trigonal bipyramidal intermediate. Ligands with a high kinetic trans effect are in general those with high π acidity (as in the case of phosphines) or low-ligand lone-pair–dπ repulsions (as in the case of hydride), which prefer the more π-basic equatorial sites in the intermediate. The second equatorial position is occupied by the incoming ligand. The third and final equatorial site is occupied by the departing trans ligand, so the net result is that the kinetically favored product is the one in which the ligand trans to the one with the largest trans effect is eliminated.[19]
- The interchange mechanism is similar to the associative and dissociative pathways, except that no distinct MLnY or MLn-1 intermediate is formed. This concerted mechanism can be thought of as analogous to nucleophilic substitution via the SN2 pathway at a tetrahedral carbon atom in organic chemistry. The interchange mechanism is further classified as associative (Ia) or dissociative (Id) depending on the relative importance of M-Y and M-L bonding in the transition state. If the transition state is characterized by the formation of a strong M-Y bond, then the mechanism is Ia. Conversely, if weakening of the M-L bond is more important in reaching the transition state, then the mechanism is Id.
An example of the Ia mechanism is the interchange of bulk and coordinated water in [V(H2O)6]2+. In contrast, the slightly more compact ion [Ni(H2O)6]2+ ion exchanges water via the Id mechanism.[23]
Effects of ion pairing. Highly charged cationic complexes tend to form ion pairs with anionic ligands, and these ion pairs often undergo reactions via the Ia pathway. The electrostatically held nucleophilic incoming ligand can exchange positions with a ligand in the first coordination sphere, resulting in net substitution. An illustrative process is the "anation" (reaction with an anion) of the chromium(III) hexaaquo complex:
\(\ce{[Cr(H2O)6]^{3+} + SCN^{-} <-> {[Cr(H2O)6], NCS}^{2+}}\)
\(\ce{{[Cr(H2O)6], NCS}^{2+} <-> [Cr(H2O)5NCS]^{2+} + H2O}\)



