10.3: The Concept of Isolobality, Carbonyl Clusters, and Ligands Related to CO
- Page ID
- 282121
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Isolobality
In the previous chapter we discussed the most simple homoleptic carbonyls. We still need to discuss more complex carbonyls, but before we do this, we will learn about the concept of isolobality. This isolobality concept greatly helps to understand and rationalize complex carbonyls, but its applications are not limited to carbonyl chemistry. It is generally very useful to predict the stability of organic and inorganic compounds. This makes it helpful in synthesis, because in synthesis it is important to be able to estimate if the target molecule is stable or not.

The concept of isolobality was developed by Roald Hoffmann, who won the Nobel prize in chemistry in 1981. It comes from the greek words “isos” meaning “similar” and “lobos” meaning lobe. Hence, “isolobal” means “similar lobes”. In his Nobel speech he defined isolobality as follows: “Molecular fragments are isolobal if the number, symmetry properties, approximate energy and shape of the frontier orbitals and the number of electrons in them are similar - not identical, but similar. “ When molecular fragments are isolobal then they can likely be combined to form a stable molecule. Thus, isolobal fragments are compatible building blocks for the construction of stable molecules. We can also say that the concept of isolobality helps us to predict when a stable bond forms. Whenever two molecular fragments are isolobal, then they will likely form stable bonds between them.
The Concept of Isolobality
Are there simple means how to estimate if two molecular fragments are isolobal? In main group chemistry the octet rule is a very helpful guide, especially for the period 2 elements for which the octet rule holds fairly strictly. The difference between the number "8" and the number of valence electrons (VE) of the molecular fragment is equal to the number of frontier orbitals and the number of electrons in it: # frontier orbitals = number of electrons in the frontier orbitals = 8 – VE(fragment). Thus, when two fragments have the same number of valence electrons, they can be considered isolobal.
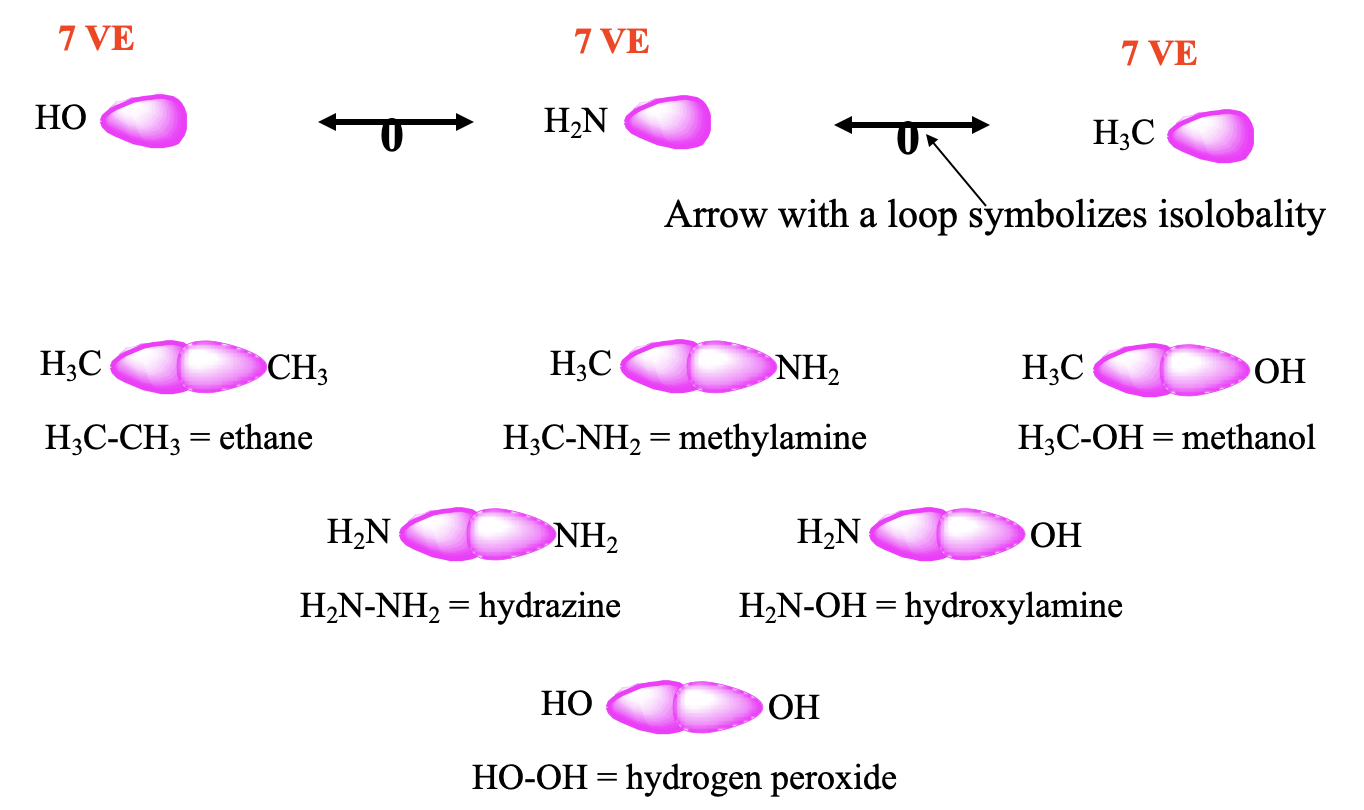
For example, the CH3 fragment has 7 VE, therefore it has one frontier orbital with one electron it (Fig. 10.3.2). The same is true for the NH2 and the OH fragments. The NH2 fragment has 5+2=7 VE, and the OH fragment has 6+1=7 VE. Therefore, these three fragments are isolobal. Isolobality between two fragments is symbolized by an arrow with a loop, and therefore we can write two such arrows between the three isolobal fragments. It should be possible to combine these isolobal fragments to form stable molecules. Let us test this. Two CH3 fragments can be combined to form an ethane molecule which is known to be stable. The combination of CH3 and NH2 gives methylamine which is stable, and the combination of CH3 and OH gives methanol, which is also stable. Two NH2 fragments give hydrazine, H2N-NH2 which exists, the combination of NH2 and OH gives the known hydroxylamine molecule NH2OH. The combination of two OH fragments gives hydrogen peroxide H2O2.
The Concept of Isolobality
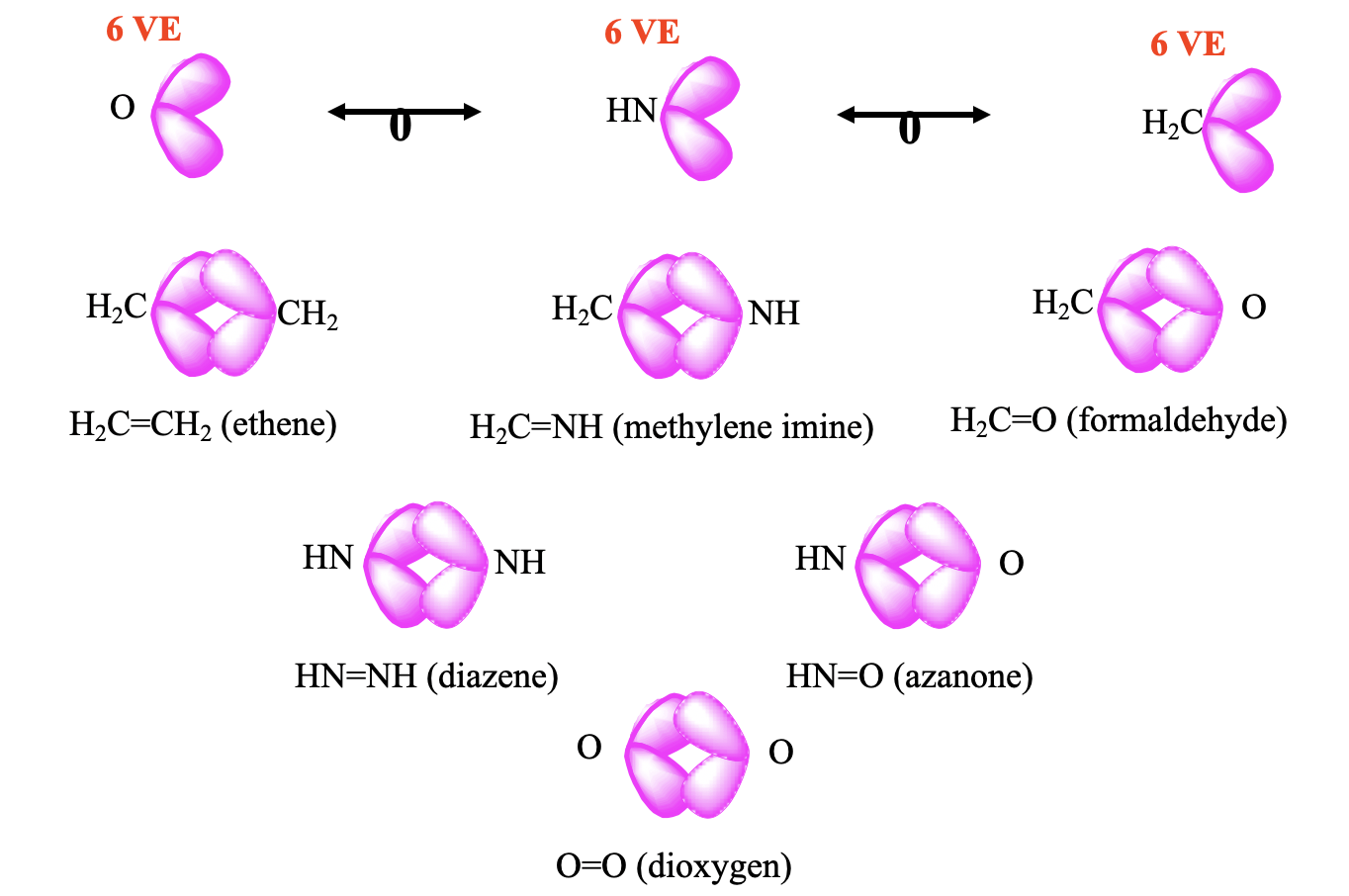
As another example, the CH2 fragment is a 6 VE fragment, thus there are 8-6=2 frontier orbitals with overall two electrons in them (Fig. 10.3.3). An NH-fragment and an O-atom also have 6 VE, and are therefore isolobal to CH2. In NH there are 5+1=6 valence electrons, and an oxygen atom has 6 valence electrons. We can combine two CH2 fragments to form ethene H2C=CH2. Combining CH2 with NH and O, respectively gives methylene imine H2CNH, and formaldehyde H2C=O, respectively. Methylene imine is stable in the gas phase, and oligomerizes in higher concentrations to form a hexamer, called urotropine. Other oligomers and polymers are also known. The combination of two NH fragments gives the known molecule diazene HN=NH, and the combination with an O atom gives H-N=O, which is known as nitroxyl or azanone, and is stable in the gas phase. The combination of two oxygen atoms gives the well known O2 molecule.
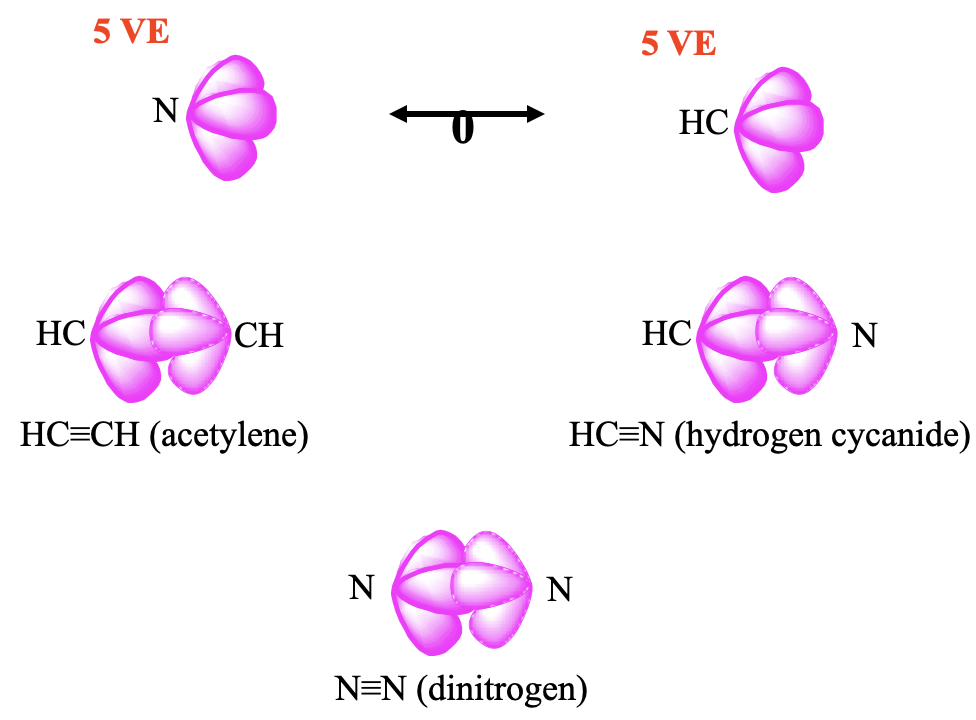
Lastly, let us look at a few 5 VE fragments (Fig. 10.3.4). The CH fragment has 4+1=5 VE, and an N-atom has 5 VE as well, thus they can be considered isolobal. Two CH fragments give acetylene C2H2, and two N atoms give the dinitrogen molecule N2. The combination of a CH fragment with an N fragment gives H-CN, well known as hydrogen cyanide.
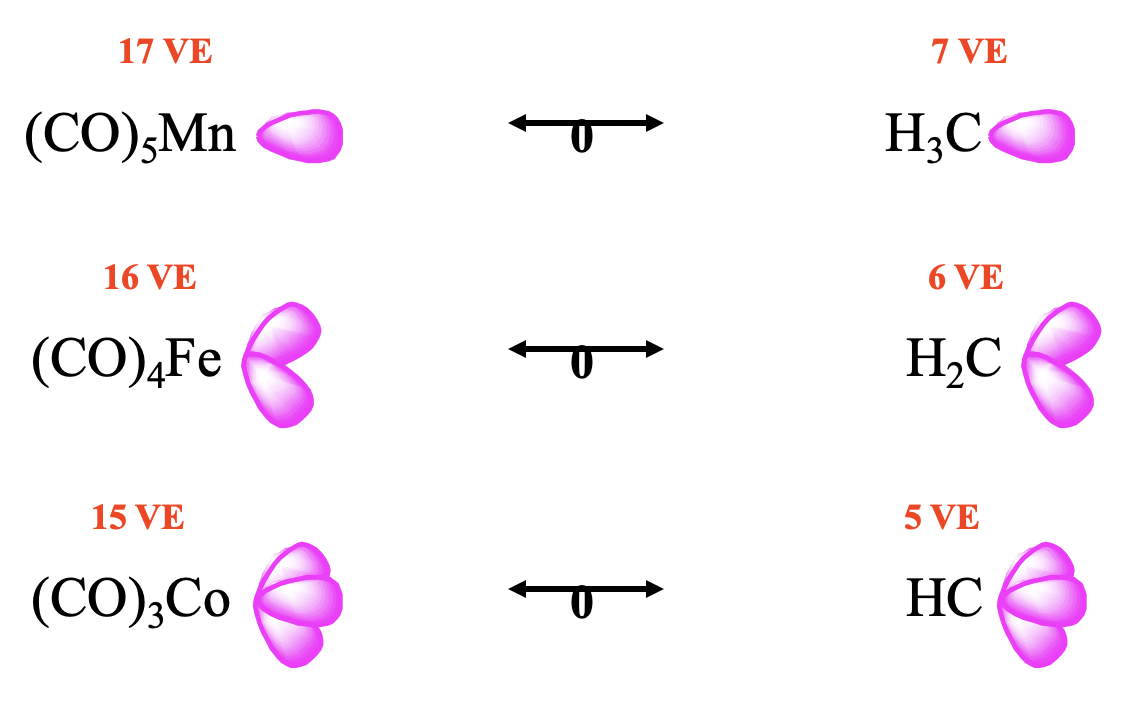
In the way the octet rule can help to predict the number of frontier orbitals and the electrons in them for main group element fragments, the 18 electron rule can be used to predict the number of frontier orbitals and electrons for organometallic fragments, including carbonyl fragments. The number of frontier orbitals and the number of electrons in them is 18 minus the number of valence electrons the organometallic fragment has: # frontier orbitals = number of electrons in them = 18-VE. For instance for a 17 VE fragment such as Mn(CO)5 there is one frontier orbital with one electron, for a 16 VE fragment such as Fe(CO)4 there are two frontier orbitals with one electron in each of them, and for a 15 VE fragment such as (CO)3Co there are three frontier orbitals with overall three valence electrons (Fig. 10.3.5). This implies that a 17 VE carbonyl fragment is isolobal to a 7 VE organic fragment such as CH3. Similarly, a 16 VE carbonyl fragment is isolobal to a 6 VE fragment such as CH2, and a 15 VE fragment is isolobal to a 5 VE fragment such as CH (Fig. 10.3.5).
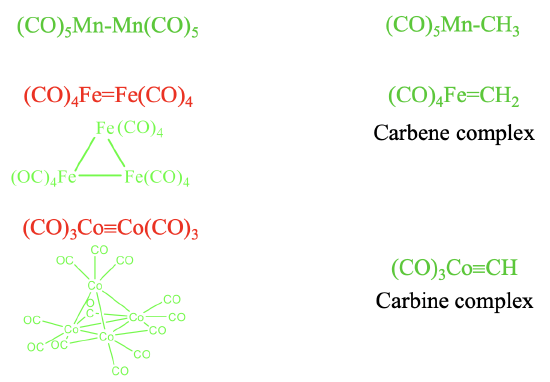
It should be possible to combine the isolobal fragments to form stable molecules. Let us check how well this works (Fig. 10.3.6). It should be possible to combine the two 17 VE electron fragments such as Mn(CO)5 to form (CO)5Mn-Mn(CO)5. This is a known molecule. Remember we encountered it previously when we discussed the homoleptic carbonyls of metals with an odd number of electrons. Combining this fragment with a 7 VE CH3 fragment leads to (CO)5Mn-CH3 which is also stable. Can we also combine two 16 VE electron fragments to form (CO)4Fe=Fe(CO)4 with an Fe=Fe double bond? The answer is no. Metal-metal double bonds, and also metal-metal triple bonds in carbonyl complexes are not formed. Instead clusters with single bonds are realized. The number of single bonds a metal makes is equal to the number of its frontier orbitals. In the case of 16 VE fragments trimeric clusters with single bonds are formed. In this cluster the two frontier orbitals of each fragment make two single bonds to two other fragments. In contrast, a 16 VE carbonyl fragment such as (CO)4Fe can be combined with a 6 VE fragment to form a compound with a Fe=C double bond. A compound with a metal-carbon double bond is called a carbene complex. Similarly, the combination of 15 VE fragments of the type Co(CO)3 does not lead to a stable (CO)3Co≡Co(CO)3 molecule with a Co≡Co triple bond. Instead, nature realizes a tetrameric tetrahedral cluster in which the three frontier orbitals of each 15 VE fragment make three single bonds to the other three 15 VE fragments. In clusters the CO ligands may not only be terminal, they can also be bridging. In the tetrameric Co-cluster, there are are nine terminal and three bridging CO-ligands. The three bridging CO ligands are connecting the three Co atoms at the base triangular face of the tetrahedron. What about the combination of a 15 VE fragment with an organic 5 VE fragment? The combination of a 15 VE fragment such as Co(CO)3 with a 5 VE organic fragment such as CH to does yield stable complexes such as the (CO)3Co≡CH complex with a Co≡C triple bond. Complexes with metal-carbon triple bonds are called carbine complexes.
Synthesis of Terameric Cluster Carbonyls
How can we make a carbonyl cluster like ((Co(CO)3)4?

It can be prepared by heating the Co2(CO)8 to a temperature above 54°C. Above this temperature the reactant loses four CO ligands and rearranges to form the cluster (Fig. 10.3.7). Interestingly, the higher homologues of the Co-cluster, the Rh4(CO)12 and the Ir4(CO)12 form spontaneously from the elements. Remember, that we previously determined that the Rh2(CO)8 and the Ir2(CO)8 are not stable. Rh and Ir favor the tetrameric clusters with 12 COs over the dimer with 8 CO ligands.
Structures of Co4(CO)12, Rh4(CO)12 and Ir4(CO)12
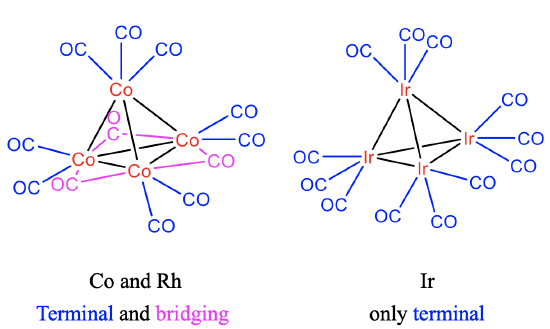
Like in the Co-cluster, there are 9 terminal and three bridging CO ligands in the Rh4(CO)12 cluster. By contrast, there are only terminal CO ligands in the iridium cluster (Fig.10.3.8) . This may be explained by the larger Ir-Ir bond length in comparison to the Co-Co and Rh-Rh bond lengths. The observation reflects the general rule that only 3d and 4d elements have bridging CO ligands, while only terminal ligands are observed in metals with 5d electrons.
Isoelectronic Charged Carbonyl Clusters
The previously discussed clusters were charge-neutral. Can we construct charged isoelectronic ones with different metals, and what is their stability? Let us start with the tetrameric Co-cluster made of four 15 VE fragments. The element left to the Co is the Fe. It has one electron less, therefore Fe(CO)3- is the 15 VE electron fragment which is isoelectronic to the neutral Co(CO)3 fragment. Its tetramer would be a Fe4(CO)124- cluster. This cluster is not known. The cluster already carries a 4- charge which is too high to support stable Fe-Fe bonds. Each Fe carries formally a 1- negative charge and there is too much electrostatic repulsion between the Fe atoms. Another possibility to realize a 15 VE fragment with Fe is a (CO)4Fe+ fragment. Here an additional ligand is added contributing two electrons, and one electron is removed resulting in a fragment with a 1+ charge. The fragment could be combined to form an Fe4(CO)164+ cluster. However, such a cluster is also not stable. This is because the coordination number would be 7, which is too high for a carbonyl. In addition, there is the destabilizing effect of the positive charge on the Fe-C bond. Similarly, tetramers of the 15 VE fragments Mn(CO)4, Cr(CO)4- and (CO)5Cr+ are also not known. Also in these cases, the coordination numbers would be too high. The Mn(CO)4 and the Cr(CO)4- would lead to a coordination number of 7, in the case of the Cr(CO)5+ fragment the coordination number would be even 8. We see here the limitations of the concept of isolobality. The presence of isolobality is not always sufficient to make a stable molecule, also other factors like coordination numbers and charge needs to be considered.What about charged isoelectronic clusters made from 16 VE? We saw previously that the neutral 16 VE Fe(CO)4 fragment gave a Fe3(CO)12 trimer. If we go from the Fe to the Mn, the isoelectronic 16 VE fragment would be a Mn(CO)4- fragment because Mn has one electron less than Fe. This fragment can indeed be trimerized to give a stable Mn3(CO)123- cluster with a 3- charge. This charge is not too high yet to destabilize the Mn-Mn bond and the coordination number of 6 is ideal for the stability of carbonyls. We could add a ligand and remove two electrons to produce a 15 VE Mn(CO)5+ fragment. However, in this case the coordination number would become 7 upon trimerization, which is too high to produce a stable cluster. In addition, the positive charge destabilizes the Mn-C bond. Replacing Mn by Cr in Mn(CO)5+ would give a neutral 16 VE Cr(CO)5 fragment, but its trimer is not stable because also in this case the coordination number becomes too high. Replacing Fe in Fe(CO)4 by Co would require a 1+ charge giving a Co(CO)4+ 16 VE fragment. Its trimer would have the coordination number 6, but it would carry a 4+ charge which is too high. A Co(CO)3- fragment would also have 16 VE, but its trimer is also not known, possibly because the relatively small coordination number of 5, which is less favorable than a coordination number of 6. Overall we can say as a rule for the stability for carbonyl clusters that there should not be positive charges, and no high negative charges. There should not be high coordination numbers.
Clusters with 16 VE and 6 VE Fragments

The cluster chemistry of carbonyls is even more versatile due to the possibility to substitute 16 and 15 VE fragments by 6 and 5 VE fragments, respectively. For instance, we can replace one 16 VE Fe(CO)4 fragment by a 6 VE CH2 fragment in the trimeric triiron dodecacarbonyl Fe3(CO)12 cluster (Fig. 10.3.9). In the resulting cluster a methylene group bridges two Fe atoms, therefore the complex can be regarded a μ-methylene complex. The substitution reduces the number of cluster valence electrons (CVE) from 48 to 38. A second substitution of another 16 VE tetracarbonyl iron fragment by another 6 VE methylene fragment gives a cluster with two Fe-C bonds and one carbon-carbon bond having 28 cluster valence electrons. This complex can be regarded as a ethene complex in which an ethene molecule binds side-on to a 15 VE Fe(CO)4 fragment. Upon binding, the two Fe-C bonds are formed at the expense of the C-C π-bond and the bond order in the C-C bond is reduced from 2 to 1. If we substitute the last tetracarbonyl iron fragment by a third CH2 unit, then a completely organic molecule, cyclopropane, results. All the molecules are known to be stable molecules, and their stability can be nicely understood by using the concept of isolobality.
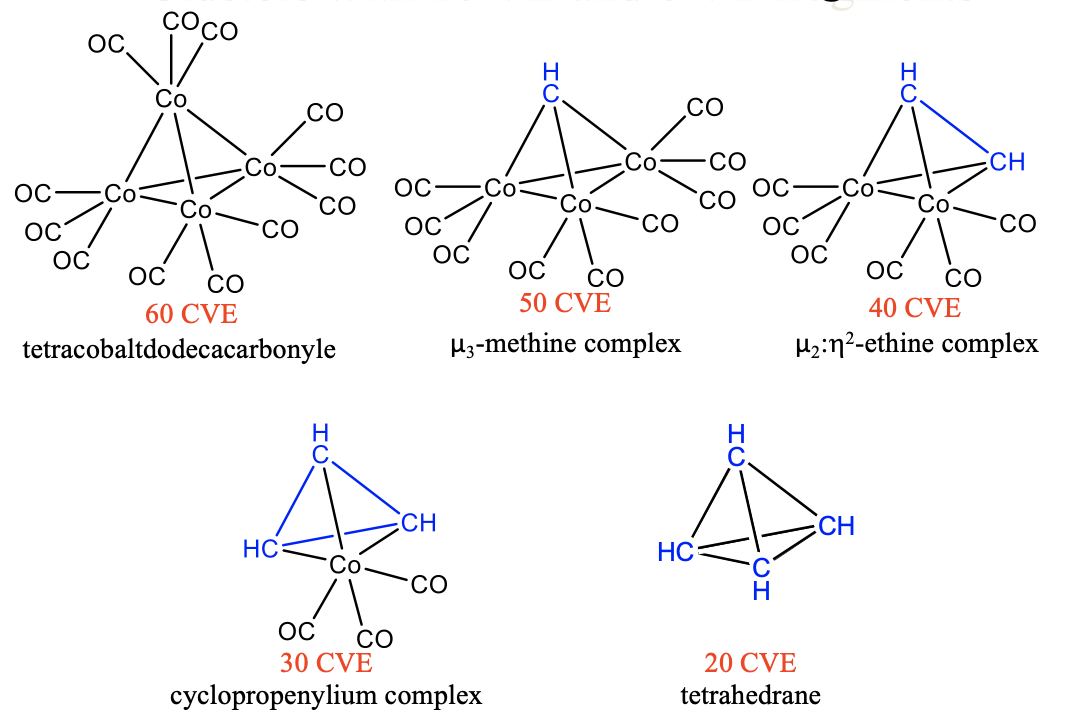
Similarly, we can substitute 15 VE tricarbonyl cobalt units by 5 VE CH fragments in tetracobaltdodecacarbonyl Co4(CO)12. A first substitution gives a 50 VE cluster with one CH fragment that makes three bonds to three Co(CO)4 fragments (Fig. 10.3.10). Because the CH group bridges three metal atoms it is regarded a μ3-methine complex. A second substitution produces a 40 VE cluster with an organic CH-CH unit that makes four bonds to two Co atoms of two 15 VE Co(CO)3 fragments. The CH-CH fragment can be considered an ethine molecule binding side-on to a dicobalthexacarbonyl fragment, whereby the two π-bonds in ethine are expended to form four Co-C single bonds. The cluster can be considered a μ2:ƞ2-ethine complex because the ethine bridges two Co atoms and both carbons are involved in the bonding with Co. A third substitution leads to a 30 CVE cluster with three CH units binding to one Co(CO)3 fragment. There are three C-C single bonds and three Co-C bonds in the cluster. The three CH units form a cyclopropenylium complex that binds side-on to a Co(CO)4 fragment. A free cyclopropenylium molecule is a 3-ring with three π-electrons that are delocalized in the ring. Therefore, the bond order in a free cyclopropenylium molecule is 1.5. In the complex the three π-electrons are being used to make the three single bonds with the cobalt atoms. The bond order in cyclopropenylium is thereby reduced from 1.5 to 1. Finally, the fourth substitution of a tricarbonyl cobalt fragment by a methine fragment yields the completely organic tetrahedrane molecule. This molecule and the others discussed before are stable. The isolobality concept lets us rationalize these complex structures easily and understand their stability.
Synthesis of Cluster Complexes From Alkynes
The view that the 40 VE clusters are alkyne clusters is not just a formal view. They can be synthesized from alkynes. For instance alkyne-dicobalt clusters are accessible from dicobalt octacarbonyl and alkynes (Fig. 10.3.11).
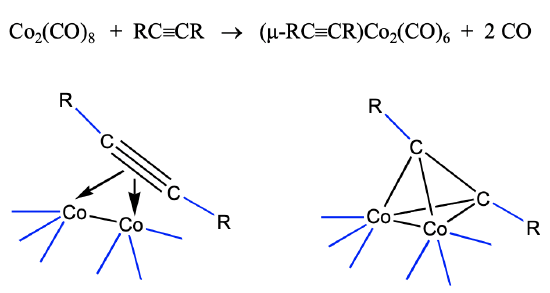
The cluster forms via the donation of the four π electrons of the alkynes into the metal d-orbitals of the dimeric cobalt carbonyl. This leads to a loss of of two CO ligands, and the formation of four Co-C bonds. Under harsher conditions the C-C triple bond can also cleave and this can give access to methine complexes.
Carbonyl Hydrides
Now let us leave the carbonyl cluster compounds and talk about another interesting class of carbonyls: carbonyl hydrides. They can be rationalized by the concept of isolobality as well. A hydrogen atom can be conceived as a species with one frontier orbital containing one electron. In this case the frontier orbital is simply the 1s orbital of the hydrogen. Thus, it should be possible to combine an H atom with a 17 VE carbonyl fragment like tetracarbonyl cobalt.
Indeed, one can combine such fragments to form stable carbonyl hydrides such as tetracarbonylhydrido cobalt (0). This molecule can be synthesized by reduction of bis(tetracarbonyl cobalt) (0) with dihydrogen (Fig. 10.3.12). Counter-intuitively, this molecule is a strong acid, it has an acidity similar to sulfuric acid. One would think that the Co-H bond would be polarized toward H based on electronegativity arguments. However, this is not the case. The carbonyl fragment has a frontier orbital which is energetically higher than that of H, and thus the bond is polarized toward H. In another view we can explain the high acidity be the fact that the loss of the proton leads to the very stable 18 VE tetrahedral Co(CO)4- anion. Thus, loss of the proton occurs easily.
Another 17 VE electron fragment is the Mn(CO)5 fragment. Also this fragment can be combined with an isolobal H fragment to form a stable molecule, which has the composition HMn(CO)5 (Fig. 10.3.13). It can be prepared from bis(pentacarbonyl manganese) and dihydrogen at 200 bar and 150°C. This carbonyl hydride is a weak acid, it has a similar acidity as H2S. We could argue that this lower acidity may be because the loss of the proton reduces its coordination number from 6 to 5. The coordination number of 6 is the preferred coordination number for carbonyls and thus the tendency to lose the proton is relatively small. The different metal and the number of carbonyl ligands will likely lead to a different energy of the frontier orbital compared to the previous example, which leads to a different polarity.
Overall, one can tune the properties in carbonyl hydrides from highly acidic to hydridic by choice of the metal the coordination number, and also by the choice of additional ligands L other than carbonyl. The electronic and steric properties of the ligands have an influence on the energy of the HOMO of the fragment, and thus on the polarity of the metal-hydrogen bond, and the acidity.
Ligands related to CO
The cyano ligand (CN-)
Now let us leave the CO ligand, consider a number of related ligands, and discuss similarities and differences compared to the CO ligand. Let us start with the cyano ligand CN-. This ligand is isoelectronic to the CO ligand. The N atom has one electron less than O, but the negative charge at the cyanide ligand compensates for that. One question we can ask is: What is the reactive end? The answer is: In analogy to the carbonyl ligand the reactive end is the carbon atom. We can explain this by the fact that the MO diagram is similar to that of CO, only the differences in atomic orbital energies are smaller due to the smaller electronegativity difference between C and N compared to C and O. Therefore, like in CO, the HOMO is represented by the electron lone pair at the C, which makes C the more reactive end. Due to the smaller electronegativity difference, the difference in energy between the lone pair at C and the lone pair at N is smaller, therefore, in contrast to CO, the cyano ligand acts far more often as a bridging ligand between two metals using both of its electron lone pairs.
Would we expect the cyano ligand to be a stronger or weaker σ-donor compared to the CO ligand? Think about it for a moment. The answer is: It is a stronger σ-donor because of its negative charge. The negative charge at the ligand increases electrostatic repulsion between the electrons, and this increases the orbital energies. Therefore, there is a stronger tendency to donate the electrons. Our next question is: Is the CN- ligand a stronger or weaker π-acceptor than CO? The energy of the π*-orbitals is higher compared to CO because of the negative charge at the ligand. Because of that, electrons from the metal cannot be as easily accepted by the ligand. Therefore, the cyano ligand is a weaker π-acceptor than the carbonyl ligand. Our last question is: Are cyano complexes more stable with metals in high or low oxidation states. Because of electrostatic arguments a cyanide anion interacts more strongly with a metal cation rather than a metal in a zero or negative oxidation state. Therefore, unlike CO, CN- does not stabilize metals in low oxidation states. It prefers to make complexes with metal in high, positive oxidation numbers.
The Nitrosyl Ligand NO
The nitrosyl ligand NO is another ligand similar to CO. It has one more electron that CO because N has one more electron than C. The additional electron makes NO an “odd” molecule with a radical electron. Like in CO and CN-, the more electropositive element is the reactive end. In the case of NO it is the N atom. The radical electron is the most reactive electron that can be most easily donated, however the electron lone pair at N may be donated in addition. In the former case, the NO is a 1-electron donor, in the latter it is a 3-electron donor. How can we tell if one or three electrons have been donated? When only one electron is donated, the electron lone pair at the nitrogen is sterically active and leads to a bent structure (Fig. 10.3.14).
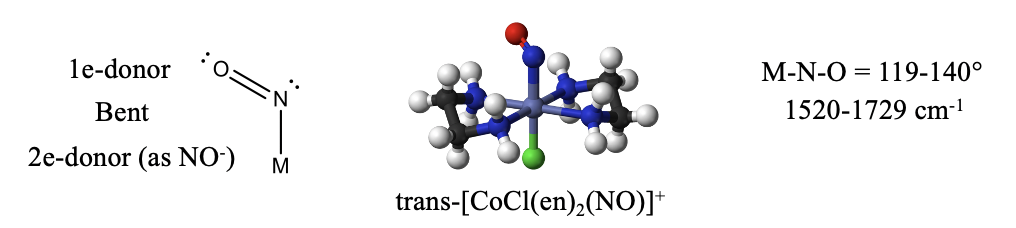
An example is the trans-bis-(ethylenediamine)chloronitrosyl cobalt (1+) cation. Generally, the O-N-M bond angle in nitrosyl complexes with NO as a 1e-donor can vary between 119 and 140°. We can also identify a bent nitrosyl ligand in the IR spectrum. Typical wave numbers are 1520-1729 cm-1.
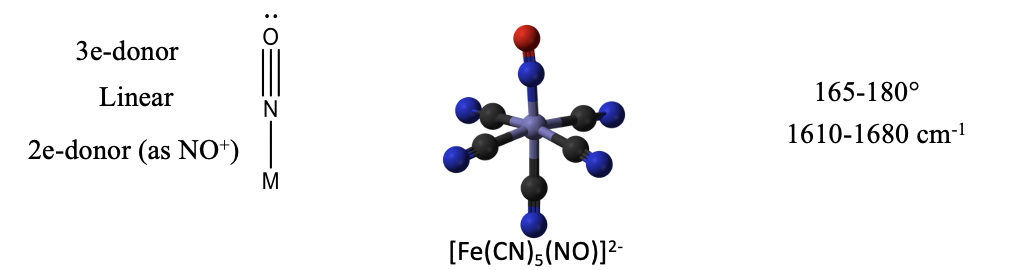
When the nitrosyl ligand donates all three electrons, then it binds to the metal in a linear fashion (Fig. 10.3.15). The electron lone pair is no longer sterically active because it is involved in the bonding. An example is the nitroprusside anion [Fe(CN)5(NO)]2-. It is used as a medication for the treatment of high blood pressure. The bond angles in complexes with NO as the 3-electron donor are often not exactly 180°, but vary between 165 and 180°. It can also be identified in the IR because it has a characteristic band between 1610-1680 cm-1.
There is a also a different view on nitrosyl complexes with linear and bent structures. In bent structures we can also consider the ligand as an NO- anion that donates two electrons. The NO- anion has two electron lone pairs at N. When it donates two electrons then one sterically active electron lone pair remains at the nitrogen atom. In linear structures we can regard the ligand also as an NO+ cation that donates two electrons. An NO+ cation has one electron lone pair at N, and when it donates that lone pair then there is no sterically active electron at the nitrogen left, and thus the ligand binds in a linear fashion.
We could also ask: What can neutral NO not be a 2-electron donor with the radical electron left at N? The answer is: The radical electron is the highest energy electron, and is always used first in interactions with a metal.
Phosphine Ligands
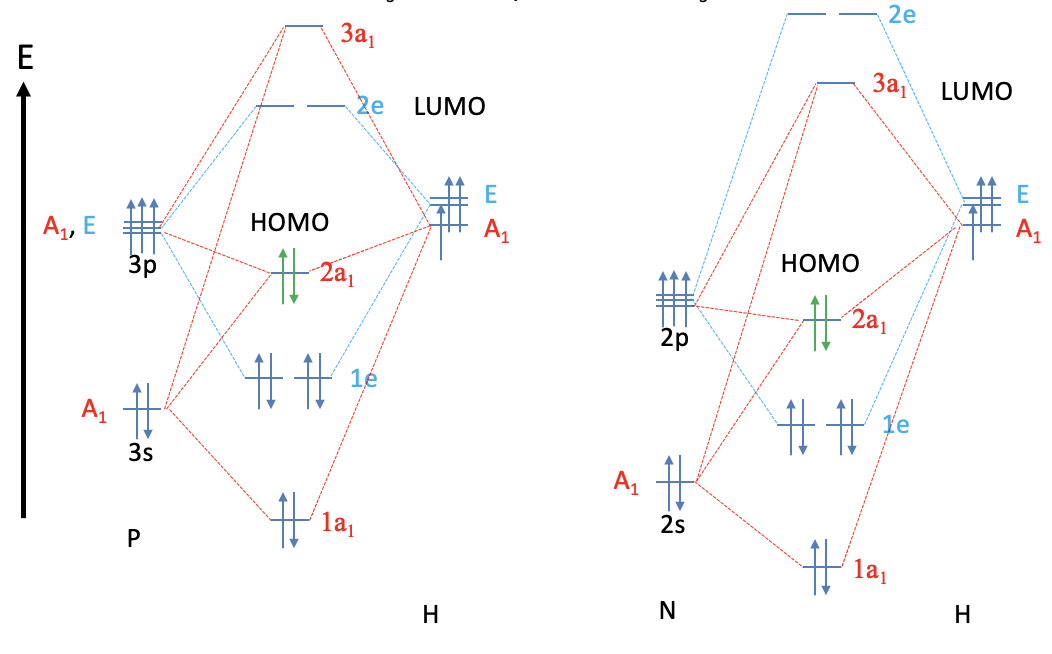
Phosphines are another class of important ligands in coordination chemistry. To approach the coordination chemistry of phosphines let us have a look at the MO diagram of the PH3 molecule and compare it with the NH3 molecule. As one would expect, the MOs are overall similar, but there is one important difference. While the LUMO in NH3 is the anti-bonding 3a1 orbital, the LUMOs in the PH3 molecule are the anti-bonding 2e orbitals. The relative energies of the 3a1 and 2e orbitals in the PH3 and NH3 molecules are swapped up. This can be attributed to the fact that the the P atom uses the 3s and the 3p orbitals as valence orbitals, while N uses the 2s and 2p orbitals. The 3s and the 3p orbitals are larger and overlap less effectively with the small 1s orbitals of the hydrogen. They also have a higher energy making the P-H bonds less polar than the N-H bonds. The energy of the PH3 HOMO is higher than that of the NH3 HOMO. Both the HOMO and the LUMO of PH3 are more diffuse and polarizable than the respective orbitals in NH3.
The higher energy of the HOMO in PH3 makes it a better donor than NH3. In addition, the PH3 has π-acceptor properties because the 2e LUMO are relatively low-lying anti-bonding 2e orbitals and have suitable shape for π-overlap with metal d-orbitals. NH3 does not have these π-acceptor properties because its LUMO is the 3a1 orbital, and not the 2e orbitals. The 2e orbitals in NH3 are energetically too high in order to allow for significant π-acceptor interactions.
Bonding in Phosphine Complexes
The σ-donor and π-acceptor properties of the phosphine ligand can be modified by substituting H by other groups. Generally, more electron donating groups increase the energy of the HOMO and the LUMO. This strengthens the σ-donor and reduces the π-acceptor properties. Vice versa, more electron withdrawing groups decrease the energy of the HOMO and the LUMO. As a consequence, the ligand becomes a weaker σ-donor and a stronger π-acceptor (Fig. 10.3.17).
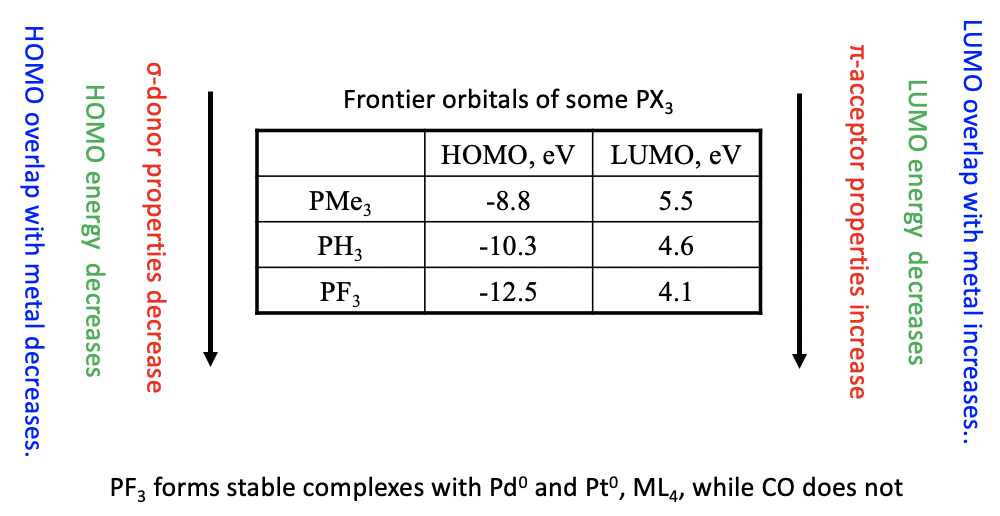
The table above shows the HOMO and LUMO energies of three phosphines. As expected the HOMO and LUMO energies decrease from PMe3 to PH3 to PF3 due to the increasingly electron-withdrawing nature of the substituent. As a consequence, the σ-donor properties weaken and the π-acceptor properties strengthen from to PMe3 to PH3 to PF3.
Not only the energies, but also the orbital overlap is important for the strength of the π-acceptor properties of the phosphine ligands. The more strongly electron-withdrawing the group is the more the anti-bonding e-type LUMO orbitals are located at the P atom. The more these orbitals are localized at P, the better they can overlap with the ligand. Vice versa the localization of the HOMO shifts toward the group as the group becomes more electron-withdrawing, thereby weakening the σ-donor properties.
Phosphine ligands with strongly electron withdrawing groups such as PF3 have π-acceptor properties strong enough to stabilize metals in low oxidation numbers, similar to CO. For example, the PF3 ligand forms stable complexes with Pd and Pt atoms in the oxidation number 0, while the respective Pd and Pt carbonyls are not known.
Dihydrogen Complexes
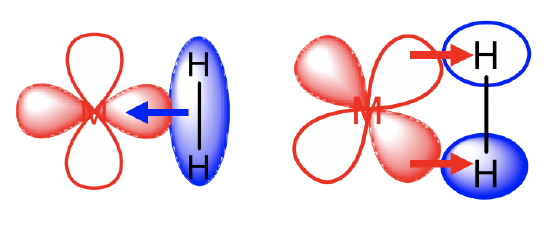
Even a simple dihydrogen molecule can serve as a ligand. We call the respective complexes dihydrogen complexes. When dihydrogen acts as a ligand, it binds side-on to the metal (Fig. 10.3.18). It uses its bonding σ-orbital for σ-donation. In addition, it uses its σ*-orbital as π-acceptor. The combination of the σ-donor and π-acceptor interactions leads to the lowering of the bond order and the lengthening of the H-H bond in the dihydrogen molecule. When these interactions are strong enough, then the H-H bond can cleave and two, separate hydrido-ligands bind to the metal via two metal-hydrogen single bonds. The π-acceptor interactions tend to be strong enough to cleave the H-H bond when the metal is relatively electron-rich. Dihydrogen complexes are therefore usually observed when the metal has a high oxidation number and/or when it has other strongly π-accepting ligands such as CO. For instance, the Mo(PMe)5H2 complex is a dihydride while the Mo(PR3)(CO)3(H2) complex is a dihydrogen complex because the latter contains three strongly π-accepting CO ligands, while the former does not.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


