10.1: Historical Background and Introduction into Metallocenes

Organometallic Chemistry

In this chapter you will get an introduction in a subfield of coordination chemistry: Organometallic chemistry. How is an orgamometallic complex defined?

Definition: Organometallic Complex

A complex with bonding interactions between one or more carbon atoms of an organic group or molecule and at least one metal atom is called an organometallic complex.

It is defined as a complex with bonding interactions between one or more carbon atoms of an organic group or molecule and at least one metal atom. It is important to understand that just the presence of an organic ligand is not sufficient to define an organometallic compound yet. There must be interactions between a carbon and a metal atom. If an organic ligand is present but no donor atom is a carbon atom, then we call this complex a metal-organic complex.

Figure \(\PageIndex{1}\): Example of organometallic vs metal-organic complexes

Let us practice this by one example: which of the following molecules are metal-organic and organometallic respectively: tetramethyl tin and tetramethoxy tin (Figure \(\PageIndex{1}\)). The former is organometallic while the latter is metal-organic. Why? This is because in tetramethyl tin there are Sn-C bonds, while in tetramethoxy tin there are Sn-O bonds.

Industrial Importance of Organometallic Compounds

Organometallic compounds are an industrially very important class of compounds. For example, aluminum and tin alkyl compounds are produced at amounts in the order of tens of thousand of tons per year. Even more important however is the use of organometallic compounds as catalysts to produce other compounds. This ranges from commodity polymers like polypropylene and polyethylene to simple organic molecules like acetaldehyde and acetic acid. These compounds are produced at a scale in the order of millions of tons per year.

History of Organometallic Chemistry

Let us take a historical approach to organometallic chemistry and see how the field has evolved. The arguably first organometallic compound was kakodyl oxide, an organo-arsenic compound.

It was accidentally produced by the French chemist Louis Cadet in 1760 when he was working on inks. He heated arsenic oxide and potassium acetate and obtained a red-brown oily liquid, known as Cadet’s fuming liquid.

Figure \(\PageIndex{2}\): Cacodyl and cacodyl oxide

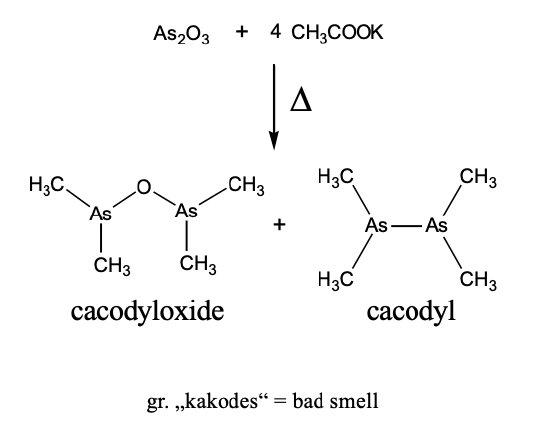
It consists mostly of cacodyl and cacodyl oxide (Figure \(\PageIndex{2}\)). In cacodyl, there is an As-As bond and two methyl groups attached to each As atom. In cacodyl oxide, there is an O atom in between the two As atoms, and each As is bound to two methyl groups. The names of these compounds come from the greek word “kakodes”=bad smell. Indeed, they have a very intense, garlic-like smell. The reaction can be used to identify arsenic in samples. For instance, if you suspected your food was poisoned with arsenic, you could heat a sample together with potassium acetate. If a bad, garlic-like smell evolved, then this would indicate that there is arsenic in your sample.

Figure \(\PageIndex{3}\): Willam Zeise (Public domain)

Another important milestone in coordination chemistry was the discovery of Zeise’s salt by the Danish chemist William Zeise in 1827 (Figure \(\PageIndex{3}\)). Zeise’s salt was the first olefin complex in which an olefin was bound side-on to a metal using its π-electrons for σ-bonding. Zeise observed that when sodium hexachloroplatinate (2-) was heated in ethanol, a compound with the composition Na[PtCl₃(C₂H₄)] could be isolated. The chemical composition of the compound suggested that there was a C₂H₄ organic fragment bonded to the platinum, but it was not clear how.

Figure \(\PageIndex{4}\): Zeise's salt: Synthesis and crystal structure.

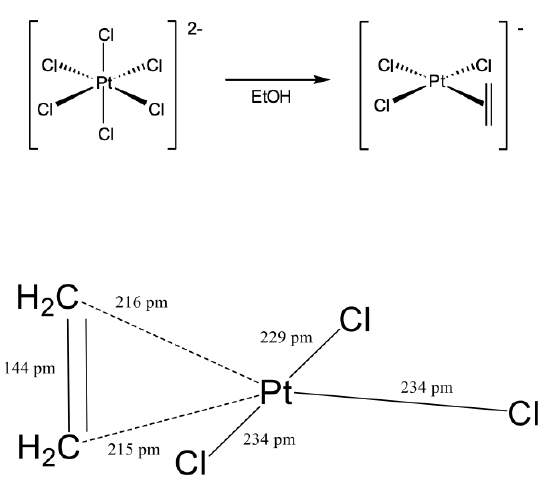
This question was only answered more than 100 years later in 1969 with the crystal structure analysis of Zeise’s salt. The crystal structure revealed that an ethylene molecule was bound side-on to the platinum (Figure \(\PageIndex{4}\)). The two carbon atoms had about the same distance to the Pt arguing that they were equally strongly involved in the bonding with Pt. The first C had a distance of 216 pm while the second carbon had a distance of 215 pm. The ethylene molecule was oriented perpendicular to the plane made of the three chloro ligands and the platinum atom. The Cl-Pt-Cl bond angles were near 90°. Overall, the structure could be described as a structure derived from a square planar structure with the ethylene as the fourth ligand that would stand perpendicular to the plane in order to minimize steric repulsion with the chloro ligands.

An important question was how to describe the bonding in the compound. It was noteworthy that the C-C bond length in Zeise’s salt was significantly longer (144 pm) than that in a free ethylene molecule (134 pm). Based on the bond-strength bond-length concept this argued that the bond was weaker than a regular C=C double bond, and that the bond order was smaller than 2. What could explain this lower bond order and the side-on coordination of the ethylene in Zeise’s salt?

Bonding in Zeise's Salt

Figure \(\PageIndex{5}\): Bonding in Zeise's salt

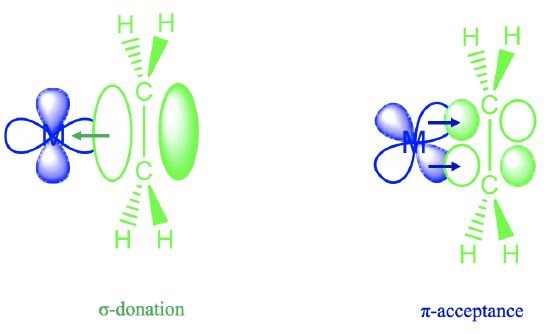
The answer is that the ethylene molecule uses its π-electrons for σ-bonding with a metal d-orbital (Figure \(\PageIndex{5}\)). You can see above that the lobe of a d_x²-y² orbital has the correct orientation to overlap with the bonding π-orbitals of the ethylene ligand in a σ-fashion. Through this interaction electron density gets donated from the bonding ligand π-orbital into the metal-d-orbital. This results in a lower electron density for π-bonding within the ligand, and thus the bond order is decreased. In addition, there is another effect that lowers the bond order. A metal d-orbital can interact with the π*-orbitals in π-fashion. In this process, electron density can be donated from the metal d-orbital into the empty π-orbitals of the ligand. The increased electron density in the π-orbitals further decreases the bond order.

In 1890, a further milestone in organometallic chemistry was reached with the synthesis of the first carbonyl complex, the nickel tetracarbonyl. Nickel tetracarbonyl is a colorless liquid that boils at 43°C.

Figure \(\PageIndex{6}\): Ludwig Mond (Public domain)

The compound was prepared by the German chemist Ludwig Mond (Figure \(\PageIndex{6}\)). Nickel tetracarbonyl forms spontaneously from nickel metal and carbon monoxide at room temperature.

Figure \(\PageIndex{7}\): Reactions associated with the Mond process

The reaction is the basis of the Mond-process that is used up to date in order to purify nickel (Figure \(\PageIndex{7}\)). Carbon monoxide gas can be streamed over impure Ni metal at temperatures of 50-60°C to form Ni(CO)₄ in gaseous form. Impurities are left behind in solid form.

Figure \(\PageIndex{8}\): Ni(CO)₄ spheres prepared through the Mond process (René Rausch, Nickel kugeln, CC BY-SA 3.0 DE)

Then, the nickel tetracarbonyl is thermally decomposed at ca. 220° to form nickel and carbon monoxide. The process can be varied to produce nickel in powder form, as spheres (Figure \(\PageIndex{8}\)), and as coatings. The Mond process is used up to date despite the very high toxicity of nickel tetracarbonyl.

Figure \(\PageIndex{9}\): Victor Grignard (Public domain)

In 1900 the first Grignard reagents were discovered. Victor Grignard (Figure \(\PageIndex{9}\)) was an enthusiastic young French chemist who discovered how to make organomagnesium halides (RMgX) while working for his Ph.D.

Figure \(\PageIndex{10}\): Grignard reaction

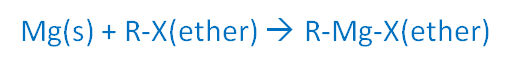
His supervisor, Sabatier, had been trying this chemistry for some time, but Victor was the genius who solved the problem. Organomagnesium halides form from magnesium and organic halides in ethers. This discovery in 1900 changed the course of organic chemistry and won Grignard and Sabatier the Nobel Prize in 1912.

Figure \(\PageIndex{11}\): Wilhelm Schlenk (Public domain)

In 1917, the first lithium alkyls were prepared by Wilhelm Schlenk (Figure \(\PageIndex{11}\)). Like Grignard reagents, lithium alkyls are very valuable reactants in synthetic organic chemistry. Lithium alkyls are very air-sensitive compounds, and some do even self-ignite in air, for example tert-butyl lithium. Therefore, they need to be handled carefully under inert gas.

Figure \(\PageIndex{12}\): The Schlenk-line (Pen1234567, Vacuum gas manifold with separate taps-diagram, CC BY 3.0)

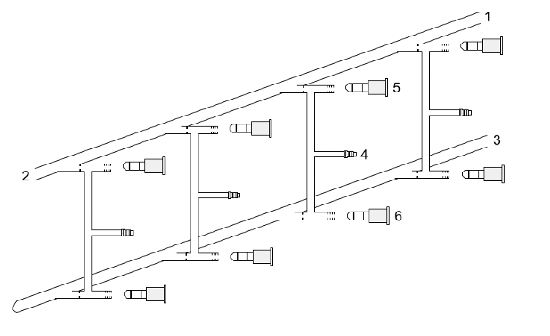
In this regard, Wilhelm Schlenk made an important invention: The Schlenk-lines (Figure \(\PageIndex{12}\)). The Schlenk lines allow to evacuate reaction flasks and back-fill them with an inert gas. A Schlenk line has a dual manifold with several ports. One manifold is connected to a source of purified inert gas, while the other is connected to a vacuum pump. The inert-gas line is vented through an oil bubbler, while solvent vapors and gaseous reaction products are prevented from contaminating the vacuum pump by a liquid nitrogen or dry ice/acetone cold trap. Special stopcocks or Teflon taps allow vacuum or inert gas to be selected without the need for placing the sample on a separate line.

The discussed discoveries were important milestones in the development of organometallic chemistry, but the field expanded only rapidly with the discovery of the first metallocene: The ferrocene. Like often in science, ferrocene was discovered through an accident.

Figure \(\PageIndex{13}\): Synthesis of ferrocene (Attribution: T.J. Kealy, P.L. Pauson, Nature 1951, 168, 1039.)

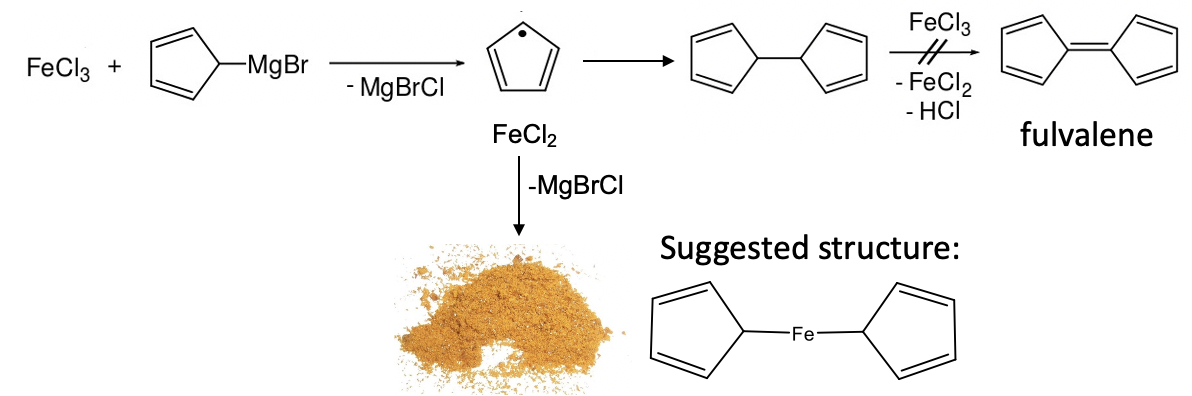
In 1951 Peter Pauson and Thomas Kealy attempted to synthesize the organic compound fulvalene through oxidative coupling of cyclopentadienyl magnesium chloride with iron (III) chloride. However, instead of obtaining fulvalene they observed the formation hydrofulvalene together with an orange powder with “remarkable stability”. Analysis of the powder showed that the chemical compound contained two cyclopentadienyl rings and one iron atom. According to the knowledge on bonding in organometallic compounds that was known at the time Kealy and Pauson suggested a structure for the molecule in which two cyclopentadienyl group were bound to a single Fe atom via two Fe-C bonds (Figure \(\PageIndex{13}\)).

However, the remarkable stability of the compound was in contradiction to this structure. The structure would be a 10 electron complex which would be highly coordinatively unsaturated. This would be inconsistent with the observed stability. We can briefly practice our electron counting skills again in order to prove that there are only 10 electrons (Figure \(\PageIndex{14}\)).

Figure \(\PageIndex{14}\): Electron counting in the wrong structure for Fe(Cp)₂

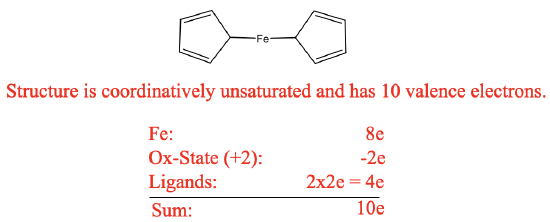
For example we can use the oxidation state method for electron counting. Fe in the neutral state has eight valence electrons. We would cleave the bonds heteroleptically which would create cyclopentadienyl anions with a 1- charge. This would mean that Fe is in the oxidation state +2, and thus we would subtract two electrons. The cyclopentadienyl anions would contribute two electrons each giving ten electrons overall. In contrast to expectations, the compound was stable in air, and could be sublimed without decomposition. Further the double-bonds in the cyclopentadienyl rings resisted hydrogenation. In addition, the structure was inconsistent with spectroscopic observations. Only one C-H stretch vibration was observed in the IR and only one signal was observed in the ¹H NMR. Kealy and Pauson’s structure would have been consistent with three C-H stretch vibrations and three NMR resonances.

Figure \(\PageIndex{15}\): Ernst Fischer (Attribution: Nobel Foundation https://www.nobelprize.org/prizes/chemistry/1973/fischer/biographical/) and Geoffrey Wilkinson (Smokefoot, Geoffrey Wilkinson ca. 1976, CC BY-SA 3.0)

For these reasons, Kealy’s and Pausons structure was soon questioned. Ernst Otto Fischer at University of Munich and Sir Geoffrey Wilkinson at Harvard University (Figure \(\PageIndex{15}\)) suggested an alternative structure that was very different from all known organometallic structures. The bonding in this structure was completely different from all bonding concepts considered thus far for organometallics.

Figure \(\PageIndex{16}\): The sandwich structure of ferrocene

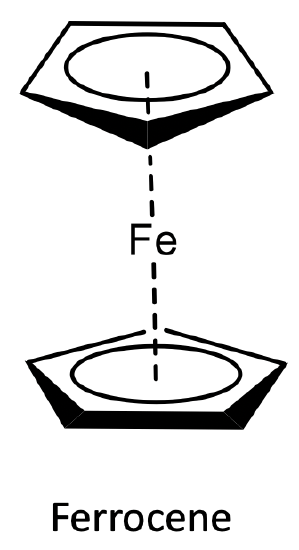
What structure did they propose? They proposed a sandwich structure in which the two aromatic cyclopentadienyl anions would sandwich an Fe²⁺ ion. What would be the bonding in this structure? The cylopentadienyl anion would donate its six π-electrons into the valence orbitals of the metal. Thus, all five carbon atoms would be equally involved in the bonding, the ligand would act as a ƞ⁵-ligand. Because of the donation of π-electrons in the cycopentadiene unit, the structure was called “ferrocene”. The ferrocene structure would explain the stability and low reactivity of the compound.

Figure \(\PageIndex{17}\): Electron counting in ferrocene using the oxidation state method

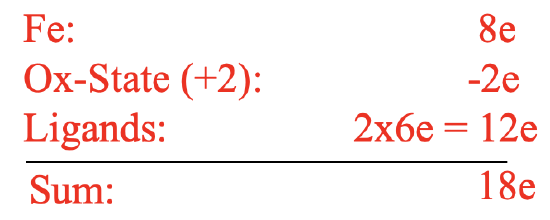
Electron-counting gives an 18 electron complex. Let us verify this using the oxidation state method. Fe would contribute eight electrons in the neutral state. The ligands would be considered as cyclopendienyl anions with a 1- charge. This would give an oxidation state of +2 for Fe reducing the number of electrons from eight to six. The two ligands would contribute six electrons each giving twelve electrons. 12+6=18. Hence, the structure fulfills the 18 electron rule. The structure is also consistent with the spectroscopic observation of one NMR resonance and one C-H stretch vibration. All these were excellent arguments to support the ferrocene sandwich structure, however they were not an absolute proof. The proof finally came with the X-ray crystal structure determination which unambiguously confirmed the sandwich structure.

Bonding in Ferrocene and MO Theory

Can the stability of the ferrocene structure also be explained by molecular orbital theory? Let us check! First, we need to decide on the point group. We will make the simplification that the two C_p cyclopentadienyl rings are in eclipsed formation, and then the point group is D_5h. Actually, the rings are in staggered confirmation and the point group is D_5d, but the energy difference is minimal, and there is a very small activation barrier between the two conformers.

\begin{array}{|c|rrrrrrrr|cc|}
\hline \bf{D_{5h}} & E & 2C_5 & 2C_5^2 & 5C_2 & \sigma _h & 2S_5 & 2S_5^2 & 5 \sigma_h  & h=20 & \\
\hline A_{1}’ & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1  & & x^2+y^2, \; z^2\\A_{2}’ & 1 & 1 & 1 & -1 & 1 & 1 & 1 & -1  & R_z & \\
E_{1}’ & 2 & 2cos(72 ^{\circ}) & 2cos(144 ^{\circ}) & 0 & 2 & 2cos(72 ^{\circ}) & 2cos(144 ^{\circ}) & 0  & (x, \; y) &  \\
E_{2}’ & 2 & 2cos(144 ^{\circ}) & 2cos(72 ^{\circ}) & 0 & 2 & 2cos(144 ^{\circ}) & 2cos(72 ^{\circ}) & 0  &  & (x^2-y^2,\; xy) \\
A_{1}” & 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1  & & \\
A_{2}” & 1 & 1 & 1 & -1 & -1 & -1 & -1 & 1  & z & \\
E_{1}” & 2 & 2cos(72 ^{\circ}) & 2cos(144 ^{\circ}) & 0 & -2 & -2cos(72 ^{\circ}) & -2cos(144 ^{\circ}) & 0  & (R_x,\;R_y) & (xz,\; yz) \\
E_{2}” & 2 & 2cos(144 ^{\circ}) & 2cos(72 ^{\circ}) & 0 & -2 & -2cos(144 ^{\circ}) & -2cos(72 ^{\circ}) & 0  & & \\
\hline \end{array}

We can define the z-axis standing perpendicular to the Cp rings, and the xy plane to be coplanar with the Cp rings.

Figure \(\PageIndex{18}\): The coordinate system for ferrocene, Fe valence orbitals, and their symmetry types.

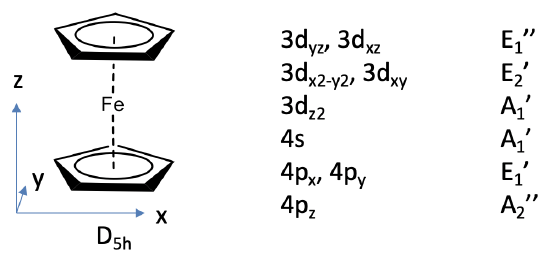
The Fe 3d, 4s and 4p orbitals will be our frontier orbitals and we can read their symmetry types from the character table of D_5h. The 3d_xz and 3d_yz have E₁’’ symmetry, the 3d_x²-y² and the 3d_xy have E₂’ symmetry, the 3d_z² has A₁’ symmetry, the 4s has A₁’ symmetry, and the 4p_x and the 4p_y orbitals have E₁’ symmetry, and the 4p_z has A₂’’ symmetry.

Next, we need to determine the ligand group orbitals. We know that the π-ligand molecular orbitals are the ones that donate the electrons into the metal-orbitals, thus we have to have a closer look at these orbitals. The π-MOs of the ligand are made from the five 2p_z orbitals of the carbon atoms that stand perpendicular to the ring. This means that there are 5 MOs to consider.

Figure \(\PageIndex{19}\): MOs of the cyclopentadienyl ligand and their relative energy

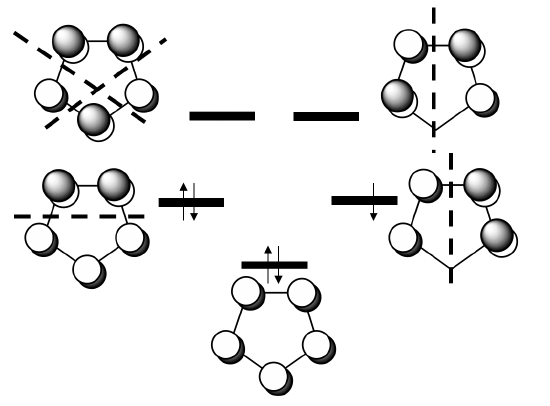
You can see the five MOs and their relative energy above. One is strongly bonding and has no node. Then, there are two double-generate weakly bonding ones that have one node, and finally there are two anti-bonding ones that have two nodes. Because the cyclopentadienyl anion has six π electrons, the bonding MO and the two weakly bonding MOs are full, the anti-bonding MOs are empty.

Because we have two Cp^- anions to consider we have overall 10 MOs to combine. We would therefore expect ten ligand group orbitals (LGOs). We can determine their symmetry type by determining the reducible and irreducible representations. The results are shown below.

Figure \(\PageIndex{20}\): 0-node LGOs

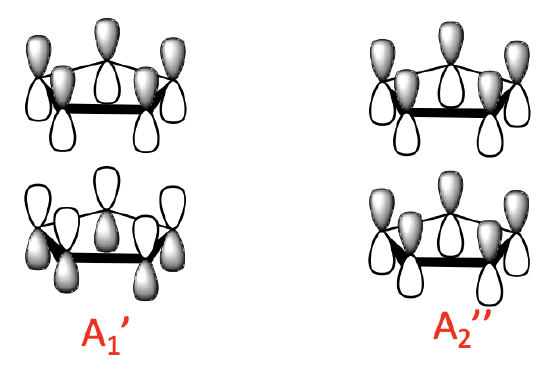
We can generally divide the LGOs into three groups with a different number of nodes. There are two 0-node LGOs with A₁’ and A₂’’ symmetry. They are made from the 0-node MOs of the ligand. There is a bonding an anti-bonding combination possible. In the bonding combination the 0–node ligand MOs have the lobes with the same algebraic sign pointing toward each other. The anti-bonding combination has the lobes with opposite algebraic sign pointing toward each other.

Figure \(\PageIndex{21}\): 1-node LGOs

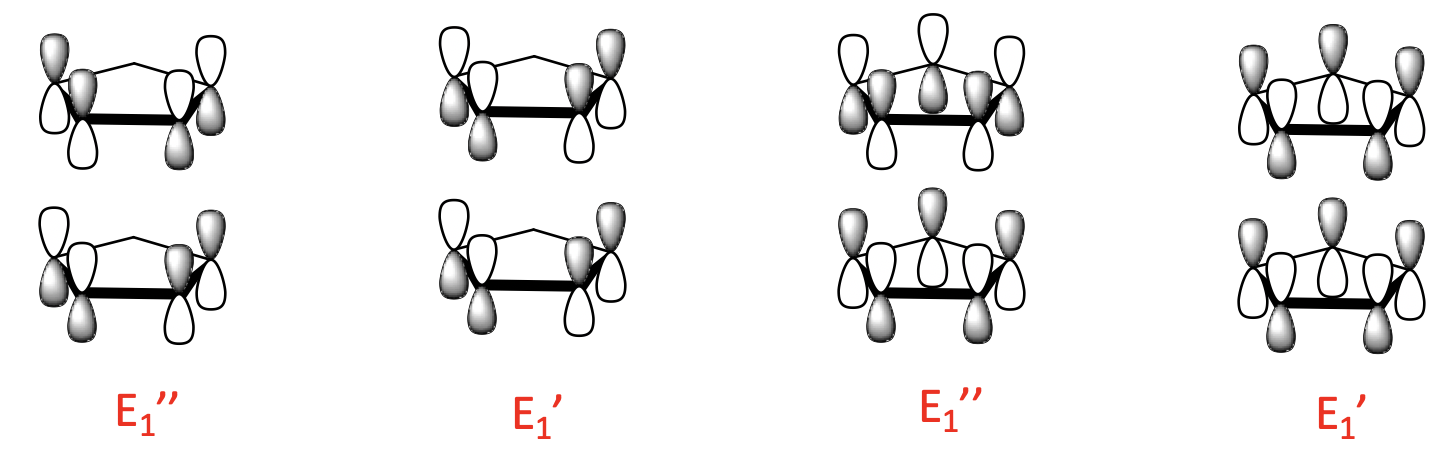
There are four 1-node LGOs with E₁’ and E₁’’ symmetry. They are constructed from the two 1-node ligand MOs. Like for the 0-node orbitals, there is a bonding and an anti-bonding combination possible.

Figure \(\PageIndex{22}\): 2-node LGOs

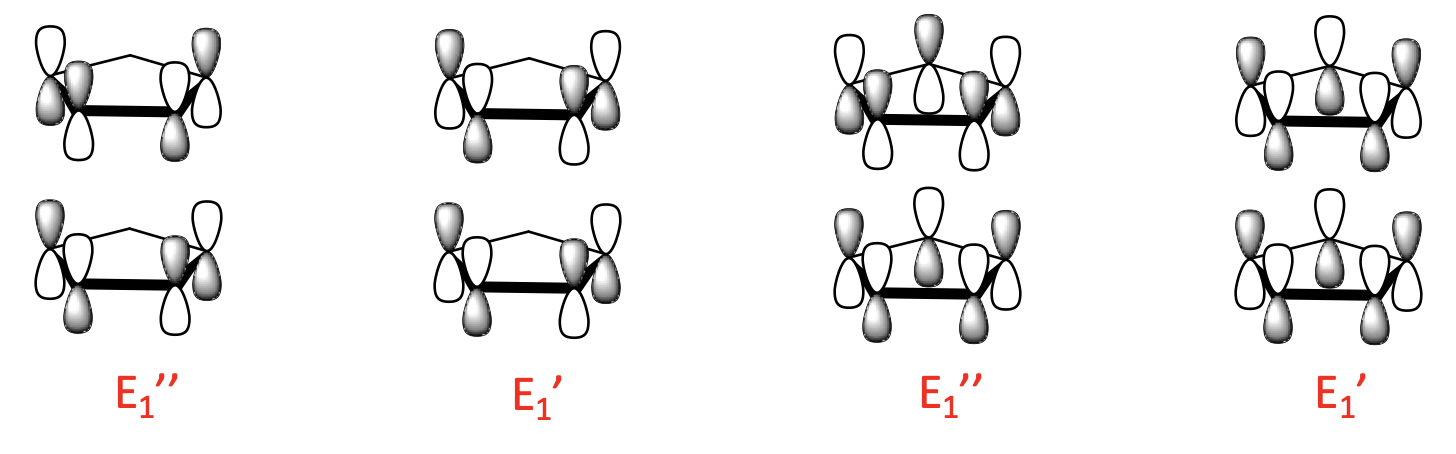
Finally, there are four 2-node LGOs with E₂’ and E₂’’ symmetry. They are made from the 2-node ligand MOs and there is also a bonding and an anti-bonding combination possible.

The Molecular Orbital Diagram of Ferrocene

Figure \(\PageIndex{23}\): MO diagram of ferrocene

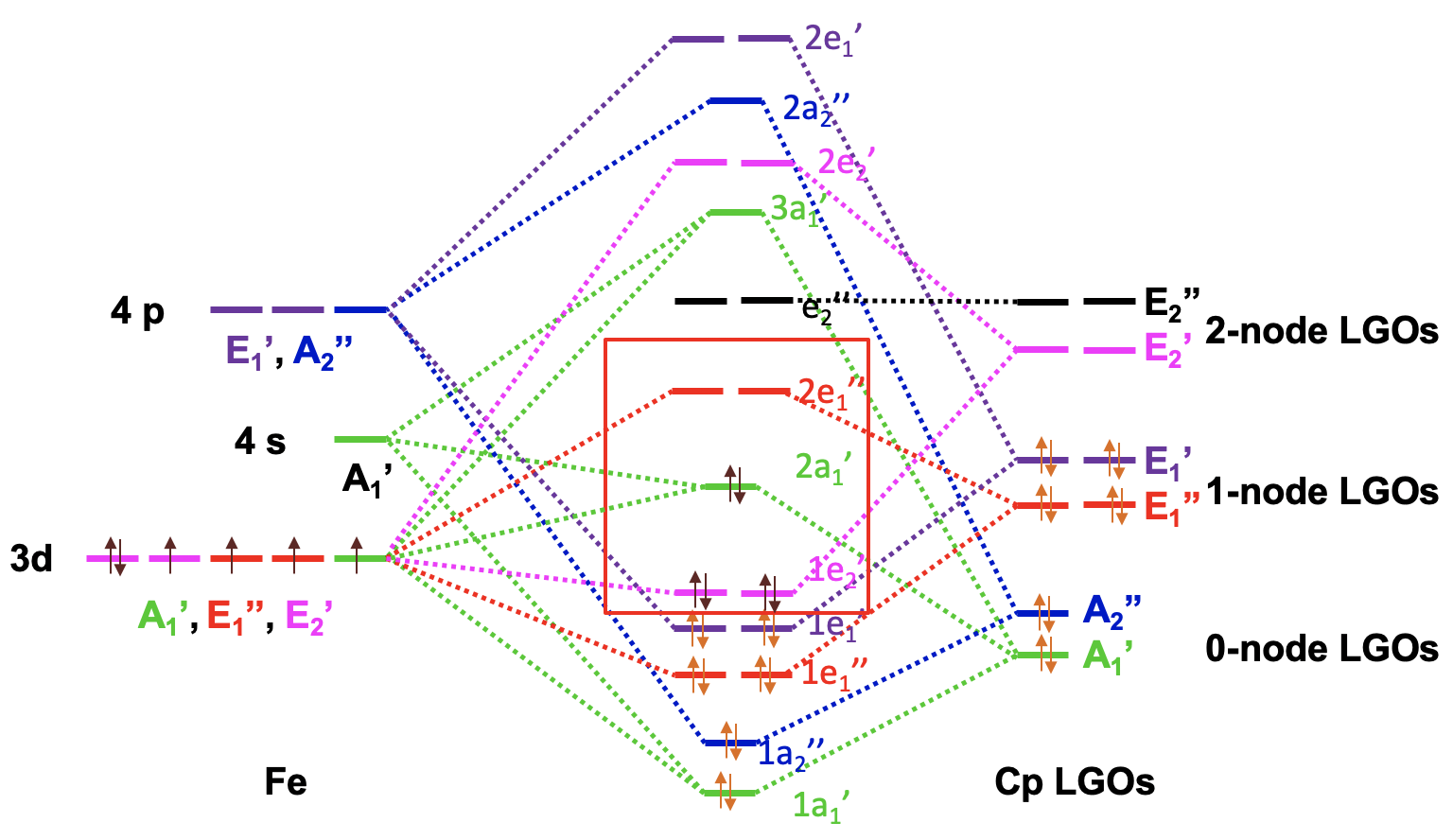
Now we have all the information to draw the molecular orbital diagram of ferrocene. As usual we plot the metal frontier orbitals on the left and label their symmetry. We plot the Cp LGOs on the right and also label the symmetry. We can order the LGOs according to energy with the 0-node LGOs having the lowest energy and the 2-node LGOs having the highest energy. Then, we can start to combine orbitals of the same symmetry type to form MOs. There are two metal AOs of the A₁’ type and one A₁’ LGO giving three MOs of this symmetry type, one bonding, one approximately non-bonding, and third one anti-bonding. We can connect AOs, LGOs, and MOs with dotted lines. Next, we can combine the A₂’’ AO and the A₂’’ LGO to form a bonding and an anti-bonding MO. We again connect the AOs, LGOs, and MOs with dotted lines. Then, we can produce two bonding e₁’’ and two anti-bonding e₁’’ MOs from the E₁’’ metal AOs and the E₁’’ LGOs and connect the orbitals with dotted lines. There are two E₁’ LGOs and two E₁’ AOs that can be combined to two bonding 1e₁’ and two anti-bonding 2e₁’ MOs and we again connect the orbitals with dotted lines. The two E₂’ LGOs can be combined with the two E₂’ d-orbitals to form a pair of bonding 1e₂’ and anti-bonding 2e₂’ molecular orbitals. Lastly, we notice that the E₂’’ LGOs do not find a partner, and we have to write them as non-bonding with the same energy into the MO diagram.

Now we need to fill the electrons into the orbitals. The ligands have twelve electrons overall. They can be filled into the six orbitals of the lowest energy. This fills the 1a₁’, the 1a₂’’, the 1e₁’’, the and 1e₁’ orbitals. We notice that all MOs are bonding which supports the stability of the molecule. We still need to consider the metal d-orbitals. We have an Fe²⁺ ion and thus six metal d-electrons. They would go into the 1e₂’ orbital which is bonding and the 2a₁’ orbital which is weakly bonding. The 2a₁ is the HOMO, and the next higher 2e₁’’ is the LUMO. We can see that we can fill all metal electrons into bonding MOs. The LUMO is an anti-bonding orbital, and thus overall all bonding MOs are filled, and no non-bonding and anti-bonding orbitals need to be filled. This is the ideal situation for a stable molecule. We can also see that the MO diagram explains the 18 electron rule. All 18 electrons are in bonding MOs.

We can consider the 1e₂’, the 2a₁’, and the 2e₁’’ metal d-orbitals in the ligand field produced by the Cp-ligands as these 5 orbitals can hold the maximum possible number of 10 d-electrons, have similar energy then the d-orbitals, and have contributions from them.

Metallocenes with other cyclic π-ligands

Is it possible to make metallocenes with other π-conjugated rings but the cylopentadienyl anion?

Figure \(\PageIndex{24}\): Bis-(benzene) chromium

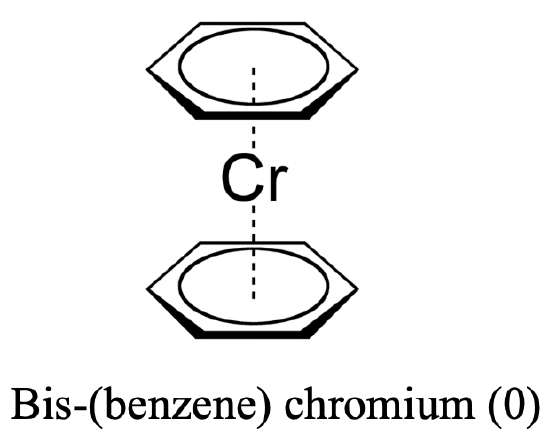
The answer is yes, for instance benzene is known to act as a ligand bis-(benzene) chromium (0). In this case the ligand acts as a ƞ⁶-ligand because all six carbon atoms are involved in the bonding. Why does chromium give stable metallocene complex with benzene? We can explain this again with the 18 electron rule. In bis-(benzene) chromium (0), chromium is in the oxidation state 0 because the benzene ligand has no charge. Thus, chromium contributes six electrons. Adding the 12 π-electrons from the two benzene ligands gives 18 electrons.

Other cyclic π-ligands

Also cyclobutadiene can act as a cylic π-ligand in complexes. The cyclobutadiene is is different from the cyclopentadienyl anion and the benzene ligand in two ways. Firstly, it has much more ring strain then the previous two, and secondly it is not an aromatic, but an anti-aromatic ligand. Remember, we have an aromatic ring when there are 4n+2 π-electrons, whereby n is an inter number. This means that rings with two (n=0), six (n=1), and ten (n=2) π-electrons are aromatic. Anti-aromatic rings are those that have 4n electrons, such as four (n=1), eight (n=2) and so forth. Cyclobutadiene has four electrons, and thus it is anti-aromatic. Anti-aromatic rings are less stable than aromatic ones because not all π-electrons are in bonding molecular orbitals. Let us illustrate this by constructing the MO diagram for the π-system of the cyclobutadiene molecule (Figure \(\PageIndex{25}\))

Figure \(\PageIndex{25}\): MO diagram for the π-system of the cyclobutadiene molecule

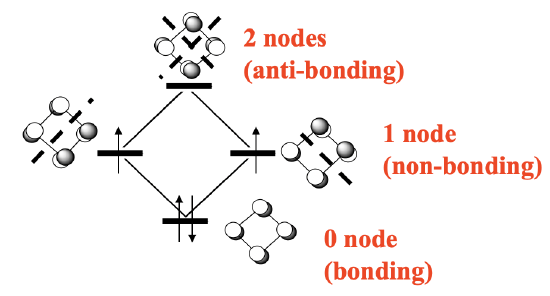
The π-system is made of four carbon atoms contributing a half-filled 2p_z orbital each (if we define the plane of the molecule as the xy plane). That makes four p-orbitals with four electrons that give four molecular orbitals. There is a bonding MO with no node, two doubly-degenerate non-bonding ones with one node, and one anti-bonding one with two nodes (Figure \(\PageIndex{25}\)). There are four electrons. We can fill two electrons into the bonding MO, but the other two must go into the two non-bonding ones under obedience of Hund’s rule.

Jahn-Teller distortion in cyclobutadiene

One may think that the cyclobutadiene is a square planar molecule because of complete delocalization of the π-electrons, but that is actually not the case. There are two shorter double-bonds and two longer single-bonds, and the shape of the molecules is a rectangle. This means that the two double bond are localized. We can view this effect as a Jahn-Teller distortion.

Figure \(\PageIndex{26}\): Jahn-Teller distortion in cyclobutadiene

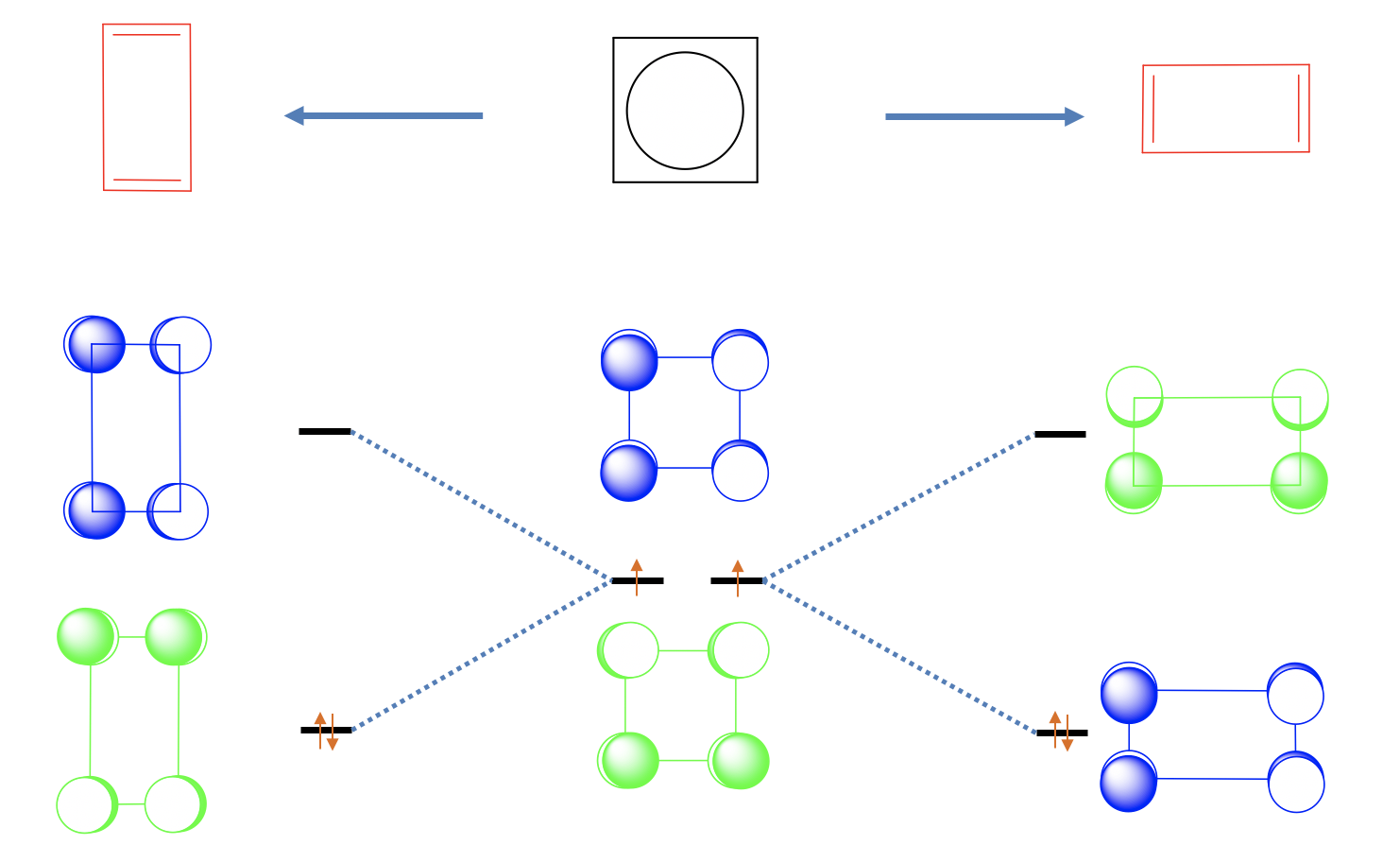
The distortion of the square to form a rectangle is energetically favorable because it lowers the energy of the two non-bonding electrons. Why? Let us look at the non-bonding orbital 1 first and elongate in x-direction, and squeeze in y-direction (Figure \(\PageIndex{26}\)). We can see that we bring the p-orbitals with bonding interactions further apart, and bring those with anti-bonding interactions closer together. This means that the energy of this orbital goes up and the orbital becomes anti-bonding. Let us do the same with non-bonding orbital 2. We see that the opposite happens. The bonding interactions are enhanced and the anti-bonding interactions are weakened. Therefore, this orbital becomes bonding and the energy goes down. We can now fill the two electrons into the bonding MO. We see that we have lowered the energy of the electrons through the distortion.

We could also have squeezed in x-direction and elongated in y-direction. In this case orbital 1 would have become bonding and orbital 2 anti-bonding. However, this distortion is symmetry-equivalent to the previous one, and does not produce a new molecule. Both molecules can be superposed by a simple 90° rotation.

Cyclobutadiene as ƞ⁴-ligand

Cyclobutadiene (Cb) in its free form is not stable because of the high ring strain and the anti-aromaticity, but complexes with cyclobutadiene as a ligand are stable. We would expect that 18 electron complexes are most stable.

Figure \(\PageIndex{27}\): Complexes with cyclobutadiene

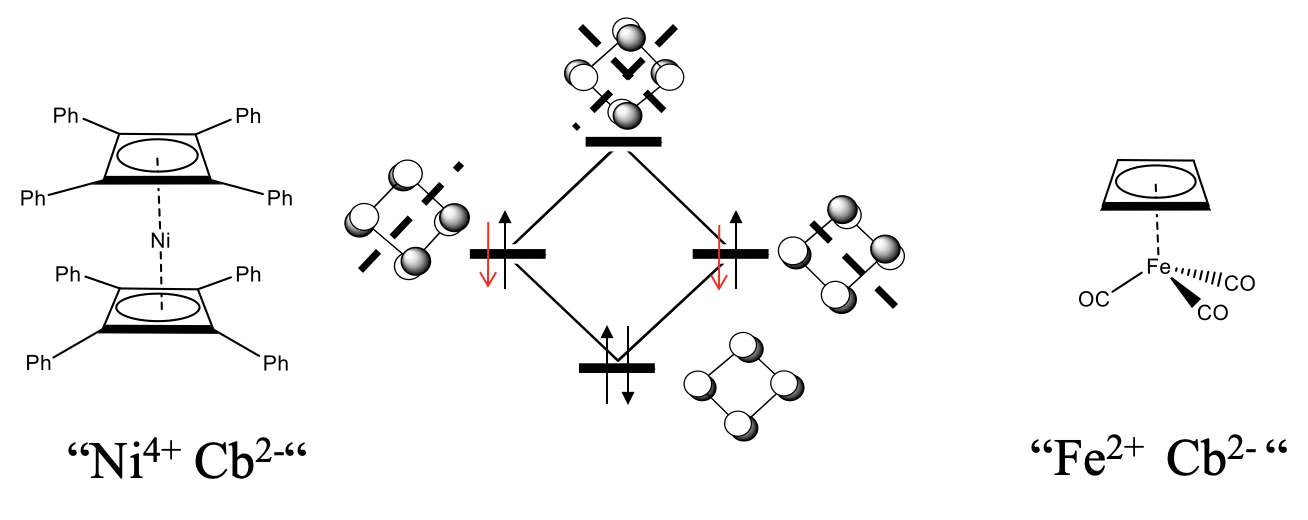
What would be an 18 electron sandwich complex with two cyclobutadiene ligands? Because each cyclobutadiene contributes four electrons, ten electrons would need to come from the metal, and we would expect a nickel cyclobutadienyl complex Ni(Cb)₂. This complex is not known, but derivatives are. For example a Ni complex with two tetraphenyl butadiene ligands are known (Figure \(\PageIndex{27}\)). Another example is the butadienyl tricarbonyl iron (0) complex. Interestingly, when cyclobutadiene acts as a ƞ⁴-ligand, then it is not distorted, but square planar. An explanation is that we can formally treat the cyclobutadiene ligand as an Cb^2- ligand binding to a metal cation. For instance in FeCb(CO)₃ the Fe would be an Fe²⁺, in the nickel complex, the nickel would be a Ni⁴⁺. The Cb^2- anion would formally aromatic because it has 4n+2=6 electrons. The additional two electrons would be in the non-bonding orbitals. Because the two non-bonding orbitals are completely filled now, there would be no longer a driving force for the distortion. Note though that is is a formal view only, and there are arguments that speak against this view. One is that the addition of the two electrons to the ligand should further destabilize the ring because the added electrons are non-bonding. Aromaticity would rather be achieved by removing two electrons to form a Cb²⁺ cation that would have only two electrons in the bonding orbital.

Cyclooctetraene (cot) as a ligand

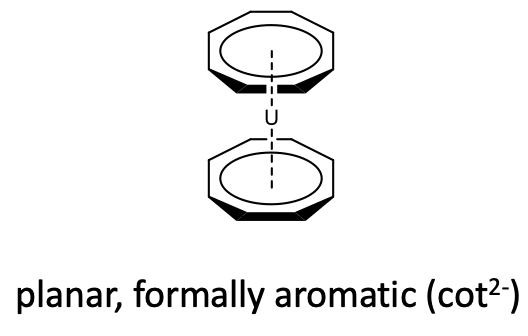
Also metallocenes with cyclooctatetraene (cot) acting as ƞ⁸-ligand is known. However, because of the large ring size only metals with large atomic radii, can make metallocenes with this ligand. For example uranium makes a uranocenes with two cyclooctatetraene ligands (Figure \(\PageIndex{28}\)).

Figure \(\PageIndex{28}\): Aromatic Cot^2- ligand

Like cyclobutadiene, cyclooctatetraene is an anti-aromatic ligand with 4n=8 π-electrons (n=2). In the free cyclooctatetraene molecule is non-planar and the π-electrons are localized (Figure \(\PageIndex{29}\)).

Figure \(\PageIndex{29}\): Free cyclooctatraene is non-planar, thus \(\pi\) electrons are localized.

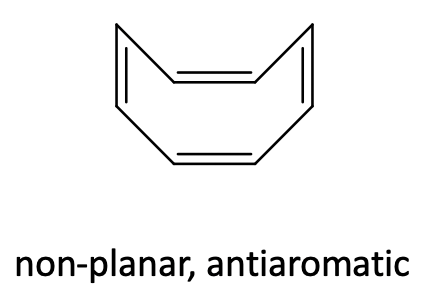
In metallocenes however, the ring becomes planar (Figure \(\PageIndex{28}\)). One can again formally explain that by assuming an aromatic cot^2- ligand that binds to a metal 2+ cation, however one should keep in mind again that this is a formal view and not necessarily reflects the bonding situation in the compound.

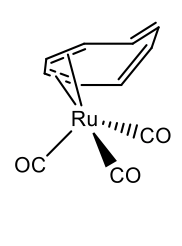
Metals having smaller atomic radius can bind to cot in ƞ², ƞ⁴, and less commonly in ƞ⁶-mode. The 18 electron rule holds in most cases. For instance, cot can make a ƞ⁴-complex in tricarbonyl cyclooctatetraene ruthenium (0) (Figure \(\PageIndex{30}\)).

Figure \(\PageIndex{30}\): tricarbonyl cyclooctatetraene ruthenium (0)

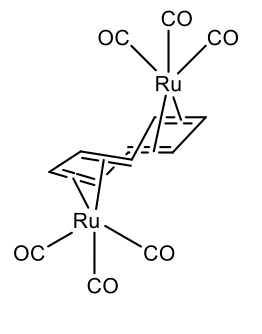
Also two metals can bind to a single cot-ligand. This is for instance realize in μ-cyclooctetraene bis(tricarbonyl ruthenium (0) (Figure \(\PageIndex{31}\)).

Figure \(\PageIndex{31}\): bis(tricarbonyl) cyclooctetraene ruthenium (0)

---

Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.