8.1: Microstates and Terms
- Page ID
- 281325
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A closer look at electronic spectra
Let us take a closer look at optical absorption spectra, also called electronic spectra of coordination compounds. We have previously argued that ligand field theory can predict and explain the electronic spectra. However, only in relatively few cases ligand field theory (LFT) is sufficient to explain the spectra. For example the hexaaqua nickel (2+) complex ion is an octahedral d8-complex ion. According to ligand field theory the metal d-orbitals in an octahedral field are the t2g and the eg–orbitals (Fig. 8.1.1). Six electrons are in the t2g orbitals, and two electrons are in the eg orbitals. Ligand field theory would predict that there is one electron transition possible, namely the promotion of an electron from a t2g into an eg orbital. This process would be triggered by the absorption of light whereby the wavelength of the light would depend on the Δo between the t2g and the eg orbitals. Overall, this should lead to a single absorption band in the absorption spectrum of the complex. We can check this prediction by experimentally recording the absorption spectrum of the complex (Fig. 8.1.1).
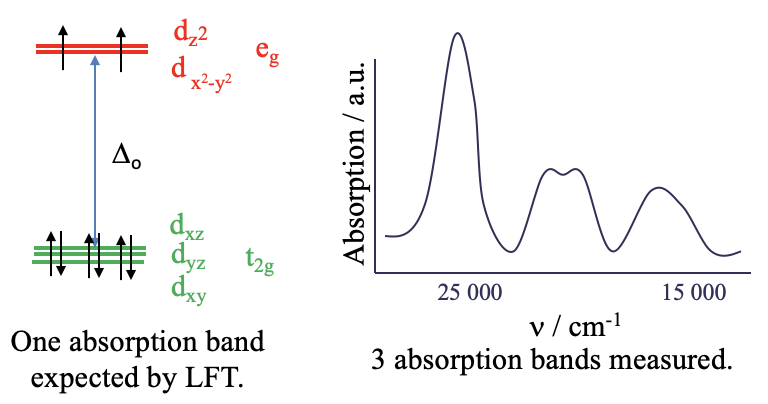
What we find is that the absorption spectrum is far more complex than expected. Instead of just a single absorption band there are multiple ones. Obviously, ligand field theory is unable to explain this spectrum. The question is why? The answer is: LFT assumes that there are no electron-electron interactions. However, in reality there is repulsion between electron in d-orbitals and this has an effect on their energy.
Effect of Electron-Electron Interactions
Let us look closer at this. To simplify the problem let us consider a d2 ion in an octahedral ligand field first (Fig. 8.1.2).
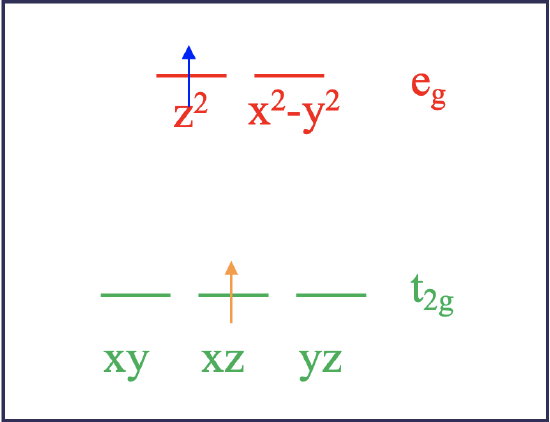

According to ligand field theory, the two electrons would be in the t2g orbitals when in the ground state. For instance, they could be in the xy, and the xz orbitals. This is called a microstate. It is called a microstate of a state because there are other combinations of orbitals possible. For example, the ground state would also be realized if the two electrons were in the xz and the yz orbitals. This combination would be another microstate associated with the ground state electron configuration. Upon excitation using light the electron in the dxy orbital could be promoted into an eg orbital, which could be either the dz2 or the dx2-y2. Those two possibilities reflect to different microstates associated with the excited state (Fig. 8.1.2). Let us assume the electron goes into the dz2 orbital. In this microstate one electron would be in the dxz orbital and the other one in the dz2 orbital. Now there us another possibility how to excite an electron. We could assume that not the dxy electron is promoted into the dz2 orbital, but the dxz electron gets promoted. In this case, we would realize a microstate in which one electron in the dxy orbital and the other one in the dz2 orbital.

Now let us compare the two cases. Ligand field theory would argue that both excited microstates have the same energy. However, in fact they do not. Why? That is because the electrons in the two excited microstates interact differently. This becomes plausible when considering the orbital shapes (Fig. 8.1.3). The dxz orbital has electron density on the z-axis, while the dxy orbital has not. Therefore, electrons in these orbitals would be expected to interact differently with an electron in a dz2 orbital which has most of its electron density on the z-axis. As a result, the two excited microstates do not have the same energy. This means that in order to promote the electron into the two different microstates we need different amounts of energies. Thus, the complex would absorb light with more than just one wavelength. This is in contrast to what ligand field theory predicts. What will we need to do in order to correctly predict how many absorption bands we get? The answer is, we must find all possible microstates for the d2 electron configuration and group those together which have the same energy. A group of microstates with the same energy is called a term. The number of electron transitions can then be predicted from the number of terms.
Russell Saunders Coupling of Electrons in Free Ions
Our task is now to find all the terms for the octahedral complex with d2 electron configuration. To simplify matters let us first look at a free d2 ion. A free ion is an ion which is not coordinated by any ligand.

The energy of the microstates depends on the quantum numbers ml and ms of the electrons (Fig. 8.1.4 and Fig. 8.1.5). This is because these quantum numbers of determine how the electrons interact. This is also called the Russell-Saunders coupling of electrons. Let us first see how the quantum number ml of the electrons influences the term symbol. The term is determined by the microstate with the highest quantum number ML, whereby ML is the sum of the quantum numbers ml of the individual electrons. The maximum ML value is also called the total orbital angular momentum quantum number L. The L value also tells you how many microstates belong to a term due to these magnetic interactions. The number of microstates is 2L+1. This is because ML can vary between –L and +L. So for instance if L=2, ML can adopt the values -2, -1, 0, +1, and +2, and that translates to 2L+1=5 microstates.
The quantum number L alone does not define the term yet. In addition, we must also consider the interaction of the spins of the electrons (Fig. 8.1.5).

The spin quantum number ms of a single electron can be either +1/2 or -1/2. When the spins of the electrons interact, their spin quantum numbers add up, defining the total spin angular momentum Ms. The microstate with the maximum Ms value defines the total spin angular momentum quantum number S. The number of microstates due to the spin-spin interactions that belong to the term is 2S+1. This is also called the spin multiplicity (Fig. 8.1.6).
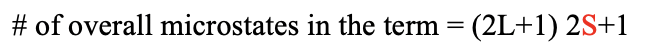
Overall the term has (2L+1)(2S+1) microstates. The total orbital angular quantum number L and the total orbital spin quantum number S define the term symbol (Fig. 8.1.7).
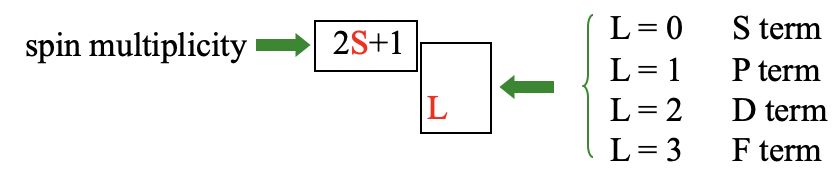
When L=0 we have an S term, when L=1, we have a P term, when L=2, we call it a D term, and when L=3 we call it an F term. These symbols are chosen in analogy to the symbols s, p, d, and f for orbitals. The spin multiplicity 2S+1 is then written as a superscript in front of the letter defined by L. This gives the overall term symbol for a term. We call a term with a spin multiplicity of 1 a singlet term, when 2S+1=2, we call the term a doublet term. A term with a spin multiplicity of three is called a triplet term, one with a spin-multiplicity of 4 a quartet term, and so forth.
Microstates for a free d2 ion
What are the possible microstates and the overall number of microstates for a free ion with d2-electron configuration? We can express this in a so-called microstate table (Fig. 8.1.8).
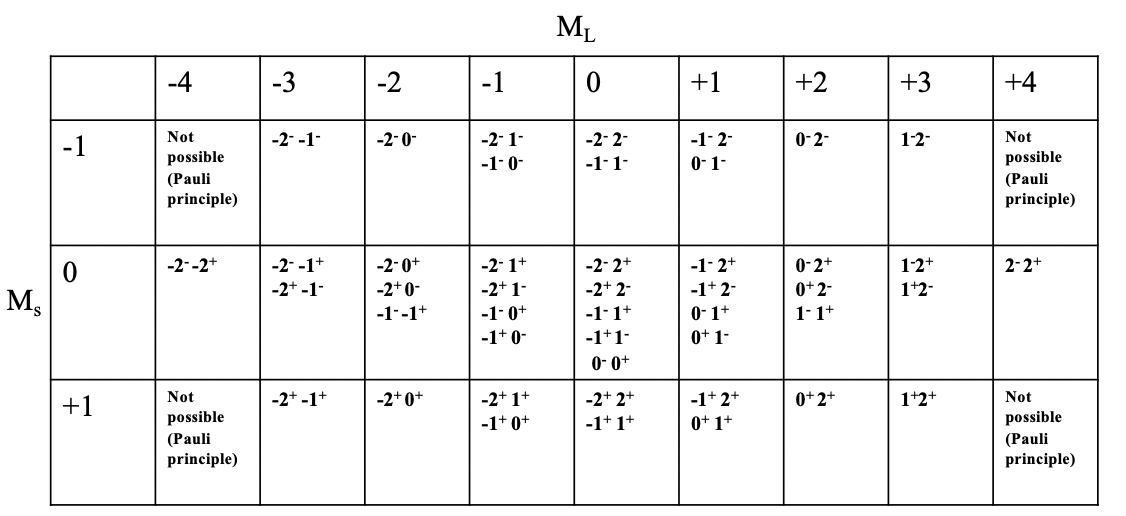
You can see the microstate table for the d2 electron configuration depicted above. Each column represents a possible value ML. For the d2 configuration, ML can adopt values from -4 to +4, hence there there are 9 columns. Each row represents possible Ms value. For the d2 electron configuration, Ms can vary between +1 and -1. +1 means both electrons have the spin +1/2, 0 means one electron has the spin +1/2 and the other one has the spin -1/2. The Ms value of -1/2 is adopted when both electrons have the spin -1/2. Now we can combine each Ms value with each ML value which defines a particular field in the table. You can see that some fields are empty due to the Pauli principle. For example, the field for ML=-4 and Ms=-1 is not filled because in this case both electrons would have the same quantum numbers, namely ml=-2, and ms =-1/2. We can further see that for some fields only one combination of electrons is possible, while for others there are multiple. For example, for the field with ML=4 and Ms=0 there is only one combination of electrons possible. You can see the symbol “2-2+” in this field. This means that the first electron has an ml value of 2 and and a spin of -1/2 and the second electron also has an ml value of 2 and an ms value of +1/2. The most populated field is the field for ML=0 and Ms=0. There are overall five microstates with that combination of ML and Ms values. If we count the overall number of microstates in the table then we arrive at the number 45. This is consistent with what we would expect according to the formula #microstates = (2L+1)(2S+1). In our example L=4 and S = 1, and thus the number of microstates is ((2x4)+1)((2x1)+1)=45. In general for a dn electron configuration with n d-electrons the number of microstates is (10!)/((10-n)!n!).
One useful property of a microstate table is that we can derive the terms and term symbols for a particular electron configuration from it. For simplification sake, we indicate a possible microstate in the table just by an “x”. Then we draw the largest possible rectangular box into the microstable that contains only fields with at least one possible electron combination (Fig. 8.1.9).
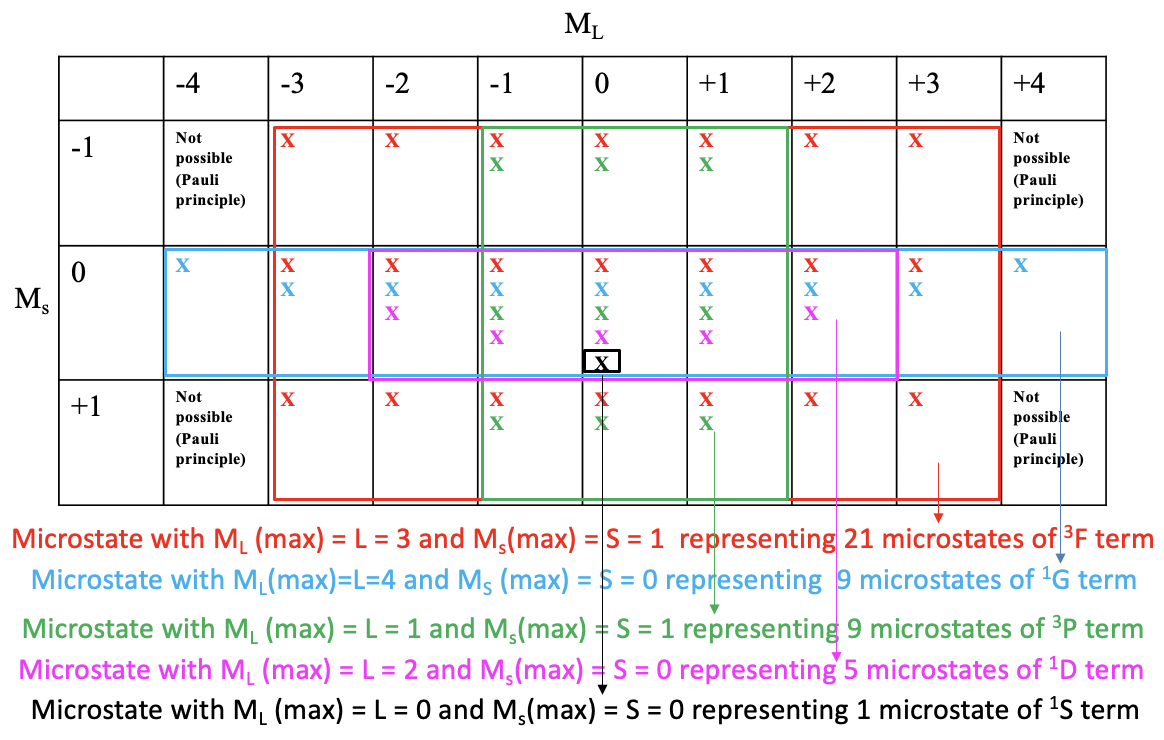
You can see that the largest possible box is the red box drawn (Fig. 8.1.9). This box contains the microstates that belong to the first term of the electron configuration d2. The number of microstates is equal to the number of fields within the red box. That makes 7x3=21 microstates. What is the term symbol for this term? In order to answer this question we need to find the microstate in the red box that has the highest ML and the highest Ms value. You can see that it is the one with ML=3 and Ms = 2. Thus, L=3 and S=1. This defines the term as a 3F term because 2S+1 = 3, and L=3 corresponds to the term symbol F. This term is a triplet term. Note that a triplet term also includes microstates with paired spins. Overall seven of the 21 microstates have Ms=0.
Next, we look what is the next-largest rectangular box we can draw, and which contains microstates we did not consider yet. We can see that the blue box contains nine fields equaling nine microstates. The microstate within this box that has the highest ML and Ms values is the one with ML=4 and Ms=0. This defines a 1G term. This is a singlet term. Note that a singlet term ONLY has microstates with paired spins (Ms=0).
There is another rectangular box which also contains nine microstates. It is the green one. The microstate with the highest ML and Ms values is the one with ML=1 and Ms=1. Thus, L =1, and 2S+1=3 which defines a 3P term. Note that despite this being a triplet term, the term also contains three microstates with paired spins.
The next-largest box is the purple one containing five fields and five microstates. What is the term with the highest ML and Ms values? It is the one with ML=2 and Ms=0. This means that L=2 and S=0 which defined a 1D term. This is a singlet term. A singlet term contains only microstates with paired spins. There is one microstate left we did not consider thus far. It is one with ML=0 and Ms = 0. These are the highest ML and Ms values because there is no other microstate. Thus, this term contains only one microstate and the term symbol is 1S. Now we have found all terms and term symbols.
The Energy of Terms
What is the relative energy of the terms? First we need to consider Hund’s rule which states that the higher the spin multiplicity, the lower the energy of a term.
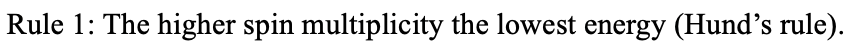
We therefore first need to rank the terms with regards to the spin multiplicity. Secondly, we need to consider the value of the total orbital angular momentum quantum number L. The higher the value the lower the energy for the term. This means that the energy of terms decreases from S, to P, to D, to F.
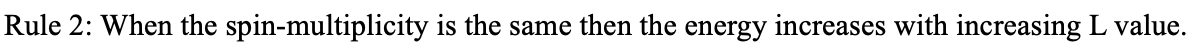
Note that this is contrary to orbital energies which increase from s, to p, to d, to f. Therefore, what would be the expected energy sequence for the terms associated with a d2 free ion? It should be: 3F<3P<1D<1S. However, the actual energy sequence is 3F<1D<3P<1G<1S. This means that, unexpectedly, the 1D term is energetically lower than the 3P term. We can understand from this is why Hund’s rule is a called a rule and not a law because there are exceptions. In most but not all cases a triplet term has a lower energy than a singlet term.
Free-Ion Terms of Other d Electron Configurations
What are the term of the other d-electron configurations (Fig. 8.1.10)?
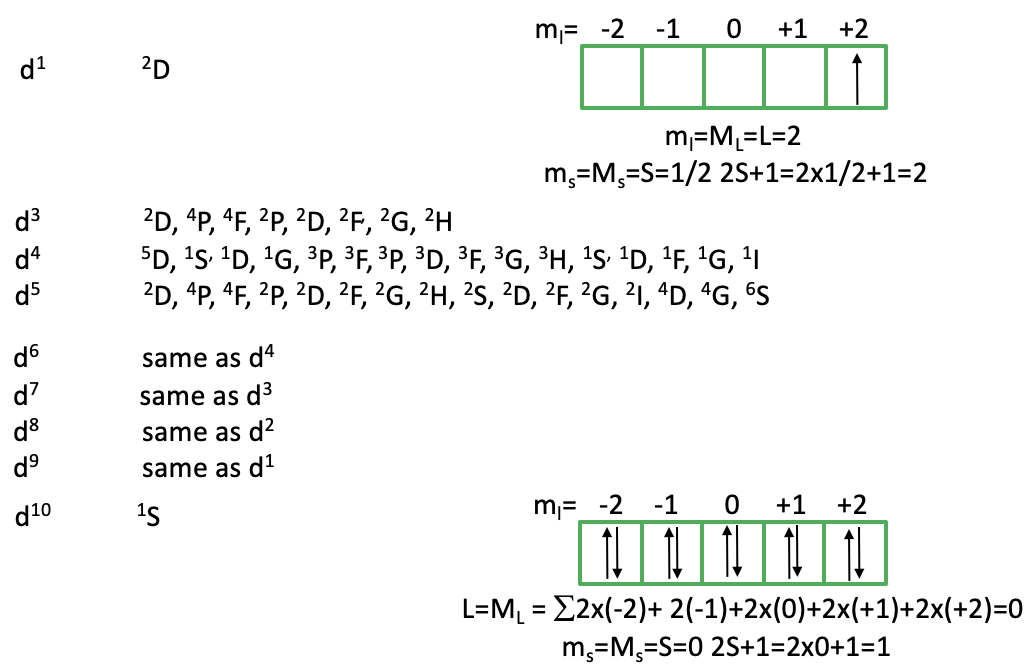
You can see above that there is only a single 2D term for a d1 free ion. How can we explain this term? Because there is no other electron, there are no electron-electron interactions, and thus every possible microstate has the same energy. This explains why there is only one term. Why is it 2D? The term symbol is determined by the microstate with the highest ML value and the highest Ms value. This is achieved when we fill the electron spin-up into the d-orbital with ml=2 (Fig. 8.1.10). Because there is only one electron, ml=ML=L=2. This makes the term a D term. It is a doublet term because Ms is maximized when the electron is spin-up or ms=+1/2. Thus, ms=Ms=S=1/2. 2S+1=2×1/2+1=2, thus we have a doublet state. How many microstates are associated with this term? (2L+1)(2S+1)=5×2=10. What does that mean? This means that we can fill the one electron that we have either spin-up or spin down in any of the five d-orbitals. All the 10 microstates are energetically equal.
When you go from d2 to d3 to d4 to d5 you can see that the number of the terms increases dramatically. This is because with increasing electron numbers the number of possible permutations increases, and thus the number of possible microstates. As a consequence, there are more terms. From d6 to d10 the number of terms decreases again. The terms for d6 are the same as the terms for d4, the d7-terms are identical to those for d3, the d8-terms are the same as the d2 and the d9-terms are the same as terms for the electron configuration d1. Why is that? This is because unoccupied states in orbitals permute the same way as occupied ones do. For instance, in the d3 electron configuration has three occupied states and seven unoccupied ones, while the d7 electron configuration has seven occupied states and three unoccupied ones. The d10 electron configuration has also only one term with the term symbol 1S (Fig. 8.1.10). Can we explain this? In the d10 electron configuration, there is no way to permute the electrons, hence there is only one microstate possible. In this microstate L=0. Why is that? When we sum up the individual ml-values of the ten electrons, then this sum is ML = L = 2×(-2)+2(-1)+2×(0)+2×(+1)+2×(+2)=0. The spin multiplicity of the term is 1 because all electrons are paired (2S+1=(2×0)+1=1). Hence, we have a singlet 1S term.
Spin-Orbit Coupling
We have still not considered all electron-electron interactions. In addition to the interaction between the angular magnetic momenta, and the magnetic interactions between the spins, there are also magnetic interactions between the angular momenta and the spins. This is called the spin-orbit coupling. It is expressed by an additional quantum number J. J can run from L+S to L-S.

The quantum number J is added as a subscript behind letter describing the term. So a full term symbol is described as 2S+1LJ. Spin-orbit coupling may lead to additional terms depending on L and S (Fig. 8.1.11).

For instance, for a 3P term, S=1, and L=1. Thus J can adopt values between L+S=1+1=2 and L-S=1-1=0. Thus, overall J can adopt the values, 0, 1, 2. This means a 3P term splits into three terms due to the spin-orbit coupling. Their term symbols are 3P0, 3P1, and 3P2. Their energy increases with increasing quantum number J. 1S and 1D terms on the other hand to do not split into additional terms. For a 1S term L+S=0+0=0, and L-S=0-0=0. The full term symbol is 1S0. For the 1D term, L+S=2+0=2 and L-S=2-0=2, thus the full term symbol is 1D2. Overall, the energy differences between terms due to J are very small, in the order of tens of wavenumbers, and orders of magnitudes smaller than energy differences due to RS-coupling, which are typically in the order of tens of thousands of wavenumbers. Thus, we usually ignore the effect of J when interpreting electronic spectra.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


