4.2: Hard and Soft Acids and Bases
- Page ID
- 274911
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Hard and Soft Bases Concept (HSAB)
The hard and soft acid and base concept (HSAB) can be conceived as a refinement of the Lewis-acid and base concept. Its most useful feature is that it can make predictions about the strength of the acid-base interactions. It can also estimate if the interactions are more ionic or more more covalent.
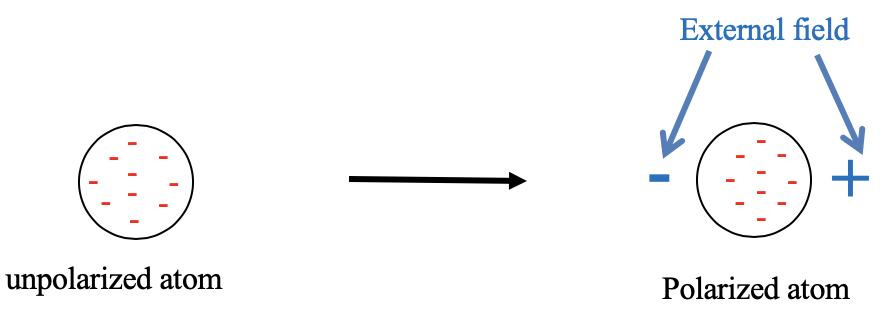
4.2.1 Visual representation of a unpolarized atom and an atom polarized in an electric field.
Let us first clarify what is meant by hard and soft, respectively. These terms refer to the polarizability of the electrons in an atom or a molecule (Fig. 4.2.1). An atom is soft when its electrons are easily polarizable. This means that the electron cloud easily deforms in an electric field. Easy deformation is consistent with the term “soft”. In an electric field the negatively charged electrons are attracted to the positive pole of the electric field. Therefore, the electron cloud distorts toward the positive end of the electric field, and the atom is polarized. Vice versa, when the electron cloud is not easily polarizable, we say the atom is hard. What is then meant by a hard and a soft acid or base? A hard or soft acid is a hard or soft Lewis acid, and a hard or soft base is a hard or soft Lewis base. As mentioned previously, the HSAB concept is useful because it make statements about the strength of the acid-base interactions, and thus the strength of the bonds. It can also make statements on whether the bonding is more covalent or more ionic (Fig. 4.2.2).

Generally, hard-hard interactions, meaning the interactions between a hard acid and a hard base, tend to be strong. The bonding is more likely ionic. Soft-soft interactions also tend to be strong, but they are more likely covalent. Hard-soft interactions tend to be weak.

Why are soft-soft and hard-hard interactions strong, while hard-soft interactions are weak? To answer this question, we must first understand what makes and acid or base hard or soft. Generally, we can say that the more delocalized the electrons are, the softer the species. For a single atom or ion this means that the larger the atom or ion is the softer the species. The larger the atom size, the more delocalized are its valence electrons. The size of a neutral atom is defined by its position in the periodic table. Generally, the higher the period, the softer the atom (Fig. 4.2.3).

For ions, also the charge plays a role. For cations, a higher positive charge makes a cation harder, for anions a higher negative charge makes the anion softer (Fig. 4.2.4).

The size of the donor/acceptor atom is not the only factor that determines the hardness. Also the ability of the species to make π-bonding is important. Species that have orbitals suitable for π-bonding tend to be soft even if size arguments suggest that they are hard. This is because π-bonding increases electron delocalization (Fig. 4.2.5).
For example, transition metals have d-orbitals available which are suitable for π-bonding with ligands, while alkali metals do not. Therefore, a relatively small transition metal cation such as Cu+ is softer than large alkali metal ions such as Cs+. For anions π-bonding is also important. For instance, CN- anions are soft bases even though the donor carbon atom is small because the CN- ligand has π-orbitals available for π-bonding with Lewis acids.
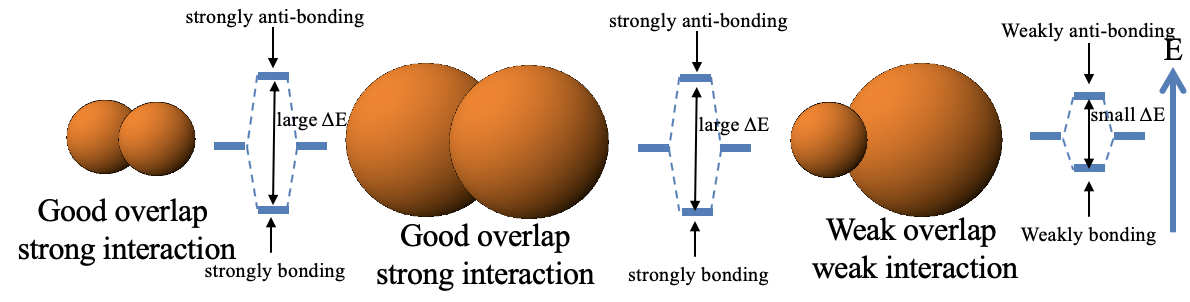
So back to the question: Why are soft-soft and hard-hard interactions strong, but hard-soft interactions weak? This essentially boils down to rule 2 of the orbital overlap criterion (see chapter 3 on MO theory). Two small orbitals have typically good overlap, and two large orbitals also have good orbital overlap, and thus the interaction is strong. However, large and small orbitals tend to have weak orbital overlap, and thus the bonding weak.
Now to the question of why soft-soft interactions tend to be more covalent, while hard-hard interactions tend to be more ionic. The answer has to do with the fact that in smaller atoms the energy differences between atomic orbitals tends to be larger compared to large atoms. As a consequence, it is statistically more likely that the HOMO and LUMO of two soft species have more similar energies compared to two hard species. When the HOMO and LUMO of a Lewis acid and a Lewis base are similar in energy, then the bonding is more covalent. When they are significantly different, then the bonding is more ionic.
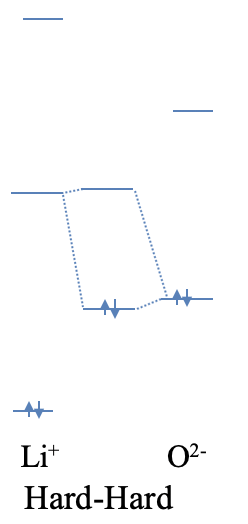
Let us illustrate this by two qualitiative examples. Lithium oxide is made of O2- anions and Li+ cations. If we view the ionic bonding between the O2- and the Li+ ions as an extreme case of a polar, dative bond, then oxide anion acts as a Lewis base, and the Li+ ion acts as a Lewis acid. How can the high ionicity be explained? Both the Li+ and the O2- are small ions, thus they are both hard. The small size also implies that the energy differences between the atomic orbitals are large. Because of this, it is unlikely that the highest occupied atomic orbital of the O2- ion has a similar energy than the lowest unoccupied atomic orbital of the Li+ ion. Due to the large energy difference, the bonding MO will be localized almost completely at the O2- anion, and the bonding will be ionic (Fig. 4.2.7).
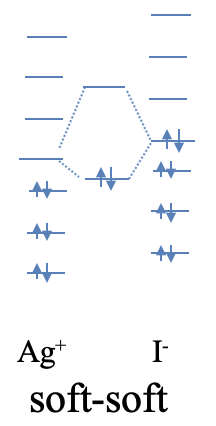
An example of a compound with strong soft-soft-interactions is silver iodide. While AgI is considered an ionic compound, the interactions have a significantly stronger covalent character. The soft nature of Ag+ is readily understood from the fact that Ag+ is a period 5 transition metal ion with low positive charge, and d-orbitals available for π-bonding. Iodine is a period 6 element, thus iodide is quite soft. Because Ag and I are elements of period 5 and 6, respectively, their orbital energy differences are significantly smaller than those of O and Li which are period 2 elements. Thus, the HOMO of I- and the LUMO of Ag+ are naturally closer in energy resulting in a more covalent interaction (Fig. 4.2.8).
We should be aware that we need to treat these considerations with caution. For example, B-O bonds are fairly covalent bonds despite the fact that B and O are both quite hard. The HOMO of the donor and the LUMO of the acceptor of hard species are not necessarily much different. Other parameters such as electronegativity differences also weigh in and must be taken into account to correctly predict the nature of the chemical bond.
Examples - Bases
To get a feeling for correctly estimating the hardness of a species let us consider a few examples. Let us start with some bases.

What statements about hardness can you make for the series F-, Cl-, Br-, I- (Fig. 4.2.9). They are all halogenide ions with the same negative charge. The size increases from fluoride to chloride, to bromide to iodide. Thus, the softness should increase in the same order. F- is a small ion with a small negative charge and should be be hard, I is a very heavy element therefore I- is very soft. Cl- and Br- are moderately hard, and soft ions, respectively.
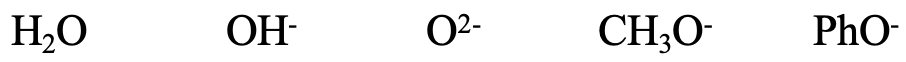
Next, consider the series H2O, OH-, O2-, CH3O-, and PhO-. All of the species contain small O donor atoms, so all of them should be considered hard. The OH- ion is somewhat softer than the H2O because of the negative charge that increases the size of the donor O atom. For the same reason O2- is somewhat softer than OH-. CH3O- is somewhat softer than O2- because of the positive inductive effect of the methyl group. The phenolate ion is the softest because the negative charge at O can be delocalized in the aromatic ring. The delocalization of the negative charge leads to a greater polarizability, and thus softness. We could also think about if F- would likely be harder or softer than H2O. F is a little smaller than O, but F carries a negative charge, so the case is ambiguous.
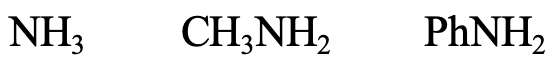
Next, let us look at the series NH3, CH3NH2, and PhNH2 (Fig. 4.2.11). The N donor atom is a small, little polarizable atom, thus the species should be regarded hard. N is somewhat larger than O though, which means that NH3 is somewhat softer than H2O. CH3NH2 would be a bit softer than NH3 because the positive inductive effect of the methyl group, and aniline would be a bit softer than methyl amine because of possibility to delocalize the lone pair at N in the aromatic ring.
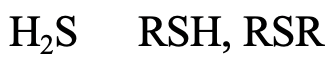
What about H2S, alkyl thiols and di alkyl thiols (4.2.12)? The S donor atom is in the 3rd period, and large enough to be considered soft. The softness would be expected to somewhat increase from H2S to R-SH to R-S-R because of the positive inductive effect of the alkyl group.
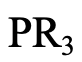
The next example is a phospine of the general formula PR3 (4.2.13). Like sulfur, phosphorus is a period 3 donor atom, and phosphines are generally soft.

Lastly, let us look at carbon monoxide and cyanide (Fig. 4.2.14). At first glance these species appear like hard bases because of the small carbon donor atoms. However, they are actually quite soft because of their ability to use their π and π* orbitals in π-bonding with Lewis acids, in particular transition metal ions. We will look closer at this issue later when we discuss the bonding in transition metal complexes in detail.
Example - Acids
Now let us think about the hardness of acids.

In the series H+, Li+, Na+, K+: Are these hard or soft acids and how does the hardness change within this series (Fig. 4.2.15)? The answer is: All alkali metal cations are considered hard acids, even the relatively large K+ cation in the 4th period. This is because alkali metal cations have only s-valence orbitals and thus a lack of orbitals suitable for π-bonding. Within the series H+ is the hardest and K+ is the softest because the ionic radius increases with increasing period.
Similarly, the earth alkaline metals Be2+, Mg2+, and Ca2+ are hard cations with the hardness decreasing from Be2+ to Ca2+. Due the the 2+ charge earth alkaline metal cations are expected harder than alkali metal cations of the same period, for example Be2+ should be estimated harder than Li+.

In the next series BF3, BCl3, B(CH3), and BH3 the hardness declines from BF3 to BH3 (Fig. 4.2.17). BCl3 is a softer than BF3 because of the smaller electronegativity of Cl versus F. The more electronegative F withdraws more electron density from the boron making it smaller, and thus harder. Because of the positive inductive effect, the B(CH3)3 is softer than BCl3. The BF3 and BCl3 molecules are considered hard acids overall, the B(CH3)3 is an intermediate case. At first glance, it would appear that BH3 is harder than B(CH3)3, nonetheless it acts more like a soft acid, possibly because of the hydride-like character of the compound.

Next let us consider the transition metal ion series Fe2+, Fe3+, Co2+, Co3+, Rh3+, Ir3+ (Fig. 4.2.18). These cations have the ability to make π-bonding, but because of the higher 2+ and 3+ charge respectively, none of them are soft. All period 4 cations with a 3+ charge, namely Fe3+ and Co3+ are hard acids, the Fe2+ and Co2+ ions are at the borderline between hard and soft due to their lower charge. Rh3+ and Ir3+ are also at the borderline. They have a higher positive charge, but are in period 5 and 6, respectively. Rh3+ would be expected to be harder than Ir3+ because it is in a lower period.

Ti4+ and Si4+ are both hard acids (Fig. 4.2.19). Generally, all ions with a charge of +4 or higher are hard acids.
What about the last series Cu+, Cd2+, Hg2+, Pd2+, and Pt2+ (Fig,. 4.2.20)? Think about it. They are all considered soft acids. Cu+ is a relatively low period 4 element, but has only a 1+ charge, and has d-orbitals for π-bonding. Hg2+, Pd2+, and Pt2+ have a somewhat higher 2+ charge, but are period 5 and 6 elements, and also have d-orbitals for π-bonding. Pt2+ would be expected softer than Pd2+ because of its higher period.
Quantitative Measures for Hardness
From the previous considerations we have seen that it is possible to make qualitative, and in some cases semi-quantitative estimates about the hardness of acids and bases, but they are not a quantitative measure for hardness. A hardness scale that allows for quantitative measure of hardness is Pearson’s concept of absolute hardness (Equ. 4.2.1).
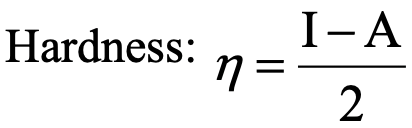
Equation 4.2.1 Equation for the quantitative calculation of absolute hardness
It relates the hardness to the difference between the ionization energy and the electron affinity over 2.
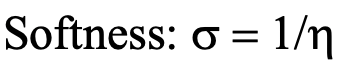
Equation 4.2.2 Equation for the quantitative calculation of softness
The softness is then defined as the inverse of the absolute hardness (Eq. 4.2.2).
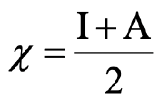
Equation 4.2.3 Equation for Mulliken's electronegativity
We can immediately see that the absolute hardness is related to Mulliken’s electronegativity scale which is the ionization energy + the electron affinity over 2 (4.2.3).
What is the idea behind this definition? We have previously qualitatively discussed that hard species tend to have large orbital energy differences, while soft species tend of have small orbital energy differences. Therefore, it makes sense to define the energy difference between the highest occupied atomic or molecular orbital and the lowest unoccupied atomic or molecular orbital a quantitative measure for the hardness of a species (Eq. 4.2.4).
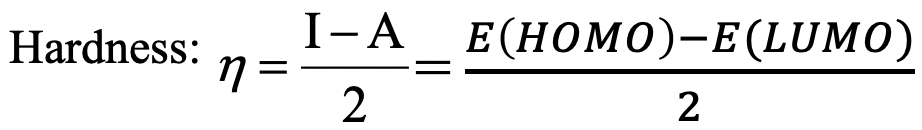
Equation 4.2.4 Extended equation for the calculation of absolute hardness
The first ionization energy IE is minus the energy of the highest occupied atomic/molecular orbital: IE=-E(HOMO or HOAO) and the electron affinity is minus the energy of the lowest unoccupied molecular or atomic orbital: EA=-E(LUMO/LUAO). Therefore, the difference between the HOMO/HOAO and the LUMO/LUAO is the same as the difference between the ionization energy and the electron affinity.
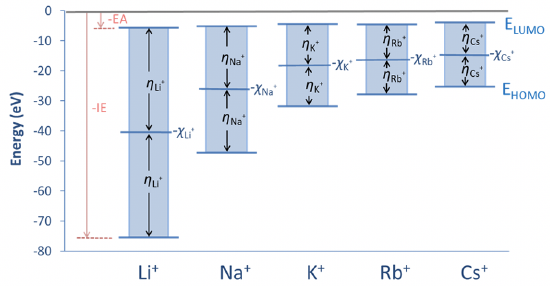
Figure 4.2.21 illustrates the concept of absolute hardness for the example of the alkali metal cations. You can see that the lowest unoccupied atomic orbitals are fairly similar in energy, but the energy of the highest occupied atomic orbital increases significantly from the Li+ to the Cs+. Thus, the energy differences decrease from the Li+ to the Cs+, and the absolute hardness η is just half the value. The energy on the y-axis half-way between the HOMO and the LUMO energy is minus the energy associated with the Mulliken electronegativity.
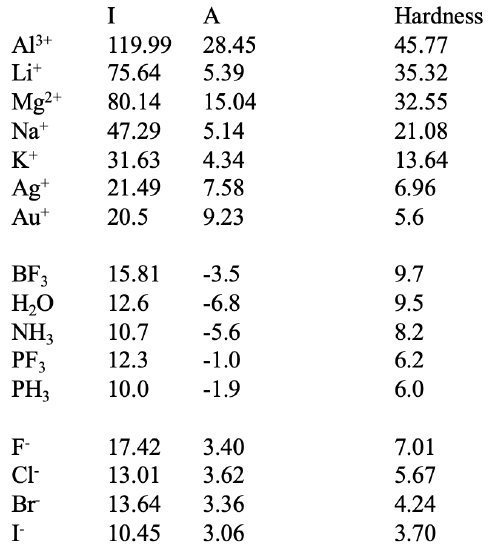
In the table above (Fig. 4.2.22) you can see a number of acids and bases together with their hardness calculated from ionization energies and electron affinities. Let us check if the calculated values are in line with expectations and see what additional value the absolute hardness concept brings. For example, we can see that Li+ is harder than Na+ which is harder than K+. This is what we expected.
We can also see that we can determine relative hardness not possible by qualitative inspection. For example, we can see that Al3+ is harder than Li+. From atomic size perspective a neutral Al is larger than a neutral Li, and from that perspective the Li+ should be harder. On the other hand the positive charge is higher on Al compared to Li. From that point of view the Al should be harder. By qualitative inspection we could not tell which parameter dominates the overall hardness. The absolute hardness concept shows that (for this case) the charge is more important than neutral atom size. Similarly we could not decide by inspection that Mg2+ was softer than Li+ because charge arguments would suggest that Mg2+ is harder while neutral atom size arguments would say that Li+ should be harder. We can see that in this case neutral atom size has a larger impact, albeit only slightly. According to our expectations Mg2+ is harder than Na+ as both ions are neighbored in the same period, and thus very similar in atomic radius, but the Mg has the higher positive charge. We can also see that Ag+ and Au+ have much lower hardness than K+ which we would expect. We would also understand the Au+ has a lower value than Ag+ because these elements are in the same group, and Au+ is in period 6, while Ag+ is in period 5.
Below Au+ you can see a group of neutral molecules. Only the BF3 molecule is a Lewis acid, other molecules are Lewis bases. We can see that BF3 has a relatively high hardness, but is softer than K+. Of the bases, H2O is the hardest base, followed by NH3, followed by PF3 followed by PH3. This is what we expected. O is the smallest donor atom, followed by N, followed by P. PF3 is harder than PH3 because of the higher electronegativity of fluorine versus hydrogen.
The last group are the halogenide anions. According to expectations F- is the hardest and I- is the softest. We can see that Cl- has a lower hardness value than PH3. The chemical behavior of latter is that of a soft base, while the former is still regarded a relatively hard base. We can see that we also need to treat the absolute hardness values with some caution, it is not an omnipotent method, other factors but HOMO and LUMO energy values can also influence polarizability.
When comparing the three groups we see that the cations tend to have the highest hardness values, followed by the neutral molecules. The anions tend to have the lowest values. This means that a hard acid tends to have a higher absolute hardness value than a hard base. To interpret the values meaningful we should therefore only compare acids with acids and bases with bases.
The HSAB Concept and Solubilities
Because the HSAB concept can estimate the strength of the interactions between Lewis acids and Lewis bases, it can also estimate a number of other properties that derive from this strength of interactions. For example, it can be used to estimate solubilities. When the Lewis acid-base interaction between cation and anion is strong we would expect low solubility, when the interaction is weak then we would expect high solubility.
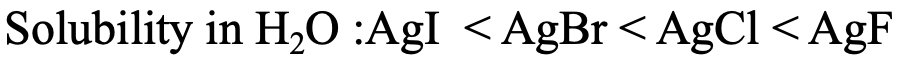
For example, it is know that the solubility of silver halogenides in water increases from AgI to AgBr to AgCl to AgF (Fig. 4.2.23). This is in accordance with the HSAB concept. Ag+ is considered soft, and thus it would make the strongest interactions with the softest anion, the iodide I-. Ag+ would make the weakest interactions with F-, because it is the hardest.
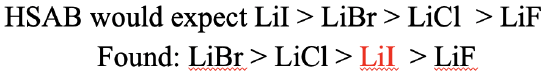
What would be our expectations for the lithium halogenides (Fig. 4.2.24)? In this case, we would expect the solubility to decline from LiI to LiBr, to LiCl, to LiF. Why? This is because Li+ is a hard cation, and thus the strongest interactions should result with F-. Consequently, LiF would have the lowest solubility. I- is the softest anion, thus it should make the weakest interactions with Li+.Consequently, the LiI would have the highest solubility. Is this what we observe experimentally? The experimentally greatest observed solubility is that of LiBr, followed by LiCl, followed by LiI. LiF has the lowest solubility. We can see that the LiI solubility is not what we expected. Instead of having the highest solubility, it has the second-lowest solubility. We can see here the limitations of the HSAB concept. There are also other factors that determine solubility, in particular solvation enthalpy. I- has a very low hydration enthalpy, which explains the lower than expected LiI solubility. In a way, the HSAB concept is able to explain the low hydration enthalpy of I- because it is based on the strength of interaction between I- and water. The water is a hard acid and therefore interacts only weakly with a soft base like I-. This can serve as an explanation for the low hydration enthalpy.
Another good example to illustrate the effects of solvation enthalpy on solubility is the solubility of the silver halogenides in liquid ammonia (not aqueous ammonia). It is actually reversed, the AgF has the smallest solubility , and the AgI has the highest solubility. The HSAB interaction between Ag+ and the halogenide ions are the same no matter of the solvent. Therefore, they cannot serve as an explanation. Rather, we can argue that the reverse enthalpies of solvation in liquid ammonia compared to liquid water are responsible for the inverse behavior. From the standpoint of HSAB, the ammonia molecules are already significantly softer than the water molecules, therefore interactions with the soft anions become significantly stronger.
The HSAB Concept and Stability
The HSAB concept can also be used to estimate thermodynamic stabilities of compounds, such as decomposition points, melting points etc. Generally, the greater the acid-base interactions the greater the expected thermodynamic stability. Let us do couple of exercises to practice this concept.
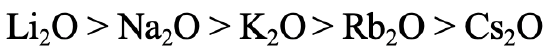
What order of thermodynamic stability would you expect for the alkali oxides (Fig. 4.2.25)? The answer is: The stability declines with increasing period of the alkali metal. Why? The oxide anion is considered a hard base due to its relatively small radius. Thus, the strongest interactions are expected with the Li+ which is the hardest alkali metal, and the weakest interactions would be expected for the Cs+ which is the softest alkali metal. This is in line with experimental observations. Only Li gives Li2O when burned in O2, Na gives sodium peroxide and the remaining alkali metals give superoxides.
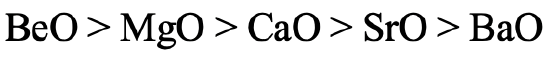
We can ask the same question for the earth alkaline oxides (Fig. 4.2.26). Similarly, the stability of BeO is the highest because Be has the highest hardness. BaO has the lowest stability because Ba2+ is the softest earth alkali cation. Ba gives barium peroxide instead of barium oxide when burned in O2.
The HSAB Concept and Acidity
The HSAB concept can also explain Brønsted acidity. How?
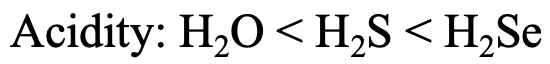
Let us look at the series H2O, H2S, and H2Se (Fig. 4.2.27). The Brønsted acidity increases from H2O to H2S to H2Se. Why? H+ is a hard acid, and therefore the strongest interactions would be expected with the hardest base, the oxide ion, and the weakest interactions would be expected with the softest base, the Se2- anion. Therefore, H2Se loses a proton most easily, making it the strongest acid. For H2O the acidity is the smallest because the interactions between H+ and O2- are the greatest.
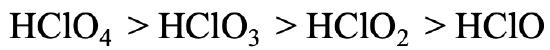
Let us go to a somewhat more complicated example (Fig. 4.2.28). The acidity of perchloric acid, chloric acid, chlorous acid, and hypochlorous acid declines from HClO4 to HClO3 to HClO2 to HClO. In this case all protons are bound to oxygen, so we cannot argue as before. However, we can argue that the negative charge in the anions of the acids is most delocalized in the case of the perchloric acid because the greatest number of resonance structures can be drawn for perchloric acid. Because the negative charge is most delocalized, the electron is most polarizable, and thus the softest. For the hypochloric acid we have the opposite case. There is no electron delocalization possible and only one resonance structure can be drawn for the hypochlorite anion. It is therefore the hardest, interacting the strongest with the proton.
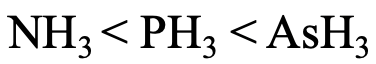
Lastly, let us think about the relative basicity of NH3, PH3, and AsH3 (Fig. 4.2.29)? The N atom is the hardest base, and the interactions with protons are the strongest. Therefore, NH3 is the strongest base. AsH3 is the weakest base because As is the softest atom making the weakest interactions with protons.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


