2.2: Point Groups
- Page ID
- 269925
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Low Symmetry Point Groups
C1 Point Group
Overall, we divide point groups into three major categories: High symmetry point groups, low symmetry point groups, dihedral point groups, and rotational point groups. Let us begin with the low symmetry point groups. As the name says, these point groups only have few symmetry elements and operations. The point group C1 is the point group with the lowest symmetry. Molecules that belong to this point group only have the identity as symmetry element.

An example is the bromochlorofluromethane molecule (Fig. 2.2.1). It has no symmetry element, but the identity. The name C1 comes from the symmetry element C1. A C1 operation is the same as the identity.
Cs Point Group
The point group Cs has a mirror plane in a addition to the identity. An example is the 1,2-bromochloroethene molecule (Fig. 2.2.2).
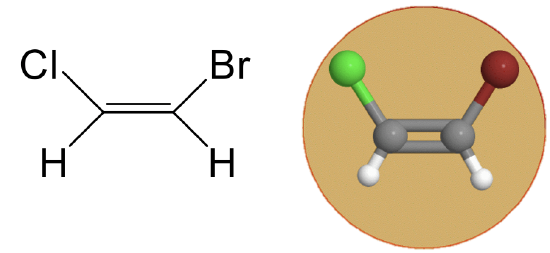 Figure 2.2.2 Cs point group of 1,2-bromochloroethene (Attribution: symotter.org/gallery)
Figure 2.2.2 Cs point group of 1,2-bromochloroethene (Attribution: symotter.org/gallery)This is a planar molecule and the mirror plane is within the plane of the molecule. This mirror plane does not move any atoms when the reflection operation is carried out, nonetheless it exists because any point of the molecule above the mirror plane will be found below the mirror plane after the execution of the operation. Vice versa, any point below the mirror plane will be above the mirror plane. This mirror plane does not have a vertical or horizontal mirror plane designation because no proper rotational axes exist.
Ci Point Group
The point group Ci has the inversion as the only symmetry element besides the identity. The point group Ci is sometimes also called S2 because an S2 improper rotation-reflection is the same as an inversion. An example is the 1,2-dibromo 1,2-dichloro ethane (Fig. 2.2.3).
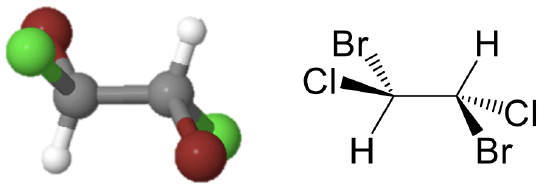
This molecule looks quite symmetric, but it has inversion center in the middle of the carbon-carbon bond as the only symmetry element. Upon execution of the inversion operation, the two carbons swap up their positions, and so do the two bromine, the two chorine, and the two hydrogen atoms.
The High Symmetry Point Groups
The symmetry elements of the high symmetry point groups can be more easily understood when the properties of platonic solids are understood first. Platonic solids are polyhedra made of regular polygons. In a platonic solid all faces, edges, and vertices (corners) are symmetry-equivalent. We will see that this is a property that can be used to understand the symmetry elements in high symmetry point groups. There are only five possibilities to make platonic solids from regular polygons (Fig. 2.2.4).

The first possibility is to construct a tetrahedron from four regular triangles. The second platonic solid is the octahedron made of eight regular triangles. The third possibility is the icosahedron made of twenty triangles. In addition, six squares can be connected to form a cube, and twelve pentagons can be connected to form a dodecahedron. There are no possibilities to connect other regular polygons like hexagons to make a platonic solid.
The icosahedron is the most complex of all platonic solids. If you would like to see and study an icosahedron from the outside and inside, there is one for study on the playground of the Allentown Cedar Beach Park, in Allentown, Pennsylvania.

The Td Point Group
The tetrahedron, as well as tetrahedral molecules and anions such as CH4 and BF4- belong to the high symmetry point group Td. Let us find the symmetry elements and symmetry operations that belong to the point group Td. First, we should not forget the identity operation, E. Next, it is useful to look for the principal axes.

The tetrahedron has four principal C3 axes (Fig. 2.2.6). It is a property of the high-symmetry point groups that they have more than one principal axis. The C3 axes go through the vertices of the tetrahedron. Because each C3 axis goes through one vertex, there are four vertices, and we know that in a platonic solid all vertices are symmetry-equivalent, we can understand that there are four C3 axes. How many unique C3 operations are associated with these axes? After three rotations around 120° we reach the identity. Therefore C33=E, and we only need to consider the C31 and the C32 rotation about 120 and 240° respectively. Because there are four C3 axes, there are four C31 and four C32 operations and eight C3 operations overall. We can express this by writing the respective numbers as coefficients in front of the Schoenflies symbol for the operations (Fig. 2.2.7).

In addition to the C3 axes there are C2 axes (Fig. 2.2.8).
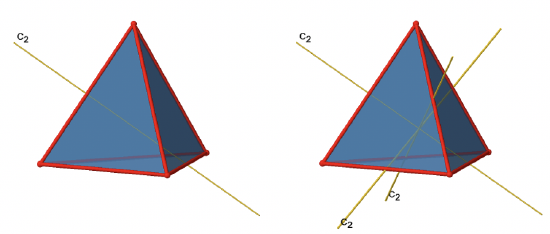
You can see that a C2 axis goes through two opposite edges in the tetrahedron. Because a tetrahedron has six edges, and each C2 axis go through two edges there are 6/2=3 C2 axes. There is only one C2 symmetry operation per C2 axis because we produce the identity already after two rotations. Therefore there are three C21 operations overall (Fig. 2.2.9).

In addition, the Td point group has S4 improper rotation reflections. Like the C2 axes, they pass through the middle of two opposite edges. This also means that they are superimposing the C2 axes. Because there are six edges, and two S4 axes per edge there are 6/2=3 S4 axes (Fig. 2.2.10).

How many operations are associated with these S4 axes? The order of the axes are even, and therefore we need four S4 operations to produce the identity. The S42 operation is the same as a C21 operation because reflecting two times is equivalent to not reflecting at all, and rotating two times by 90° is the same as rotating about 180°. Therefore overall, only S41 and S43 operations are unique operations. S42 and S44 can be expressed by the simpler operations C21 and E respectively. Because there are 3 S4 axes, there are three S41 and three S43 operations. Overall there are six S4 operations (Fig. 2.2.11).

There are also mirror planes (Fig. 2.2.11). The planes contain a single edge of the tetrahedron, thereby bisecting the tetrahedron. There a six edges in a tetrahedron, and therefore there are 6/1=6 mirror planes.
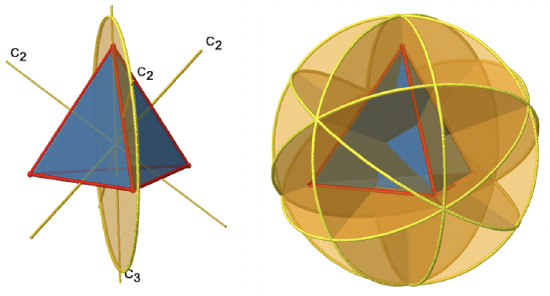
These planes are dihedral planes because each plane contains a C3 principal axis and is bisects the angle between two C2 axes. Overall, there are three C2 axes and three C2 operations. There is one reflection operation per mirror plane because reflecting two times produces the identity. Therefore, there are six σd reflection operations (Fig. 2.2.12, right and Fig. 2.2.13).

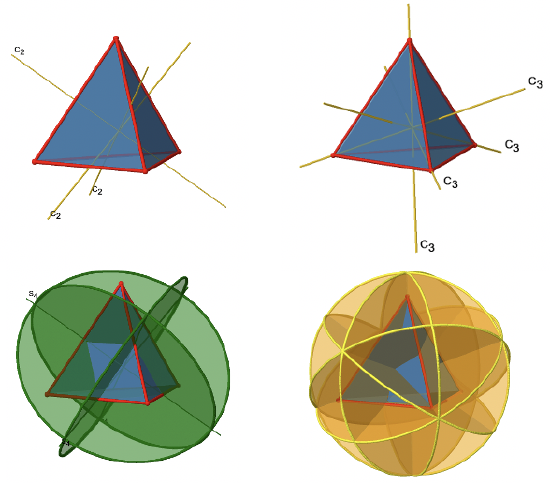
In sum (Fig.2.2.14 and 2.2.15) we can denote the overall symmetry of the Td point group the following way: E, 8C3, 3C2, 6S4, 6σd. In detail the unique symmetry operations are E, 4C31, 4C32, 3C21, 3S41, 3S43, 6σd.

The Rotational Subgroup T
The high symmetry point group T is the so-called rotational subgroup of the point group Td. A rotational subgroup is a point group in which all symmetry operations but the identity and the proper rotations have been removed from a high-symmetry point group. For the point group T this leaves the 4C3, the four C32 and the three C2 operations (Fig. 2.2.17). The S4 rotation-reflections and the mirror planes have been removed. The point group T is rare.
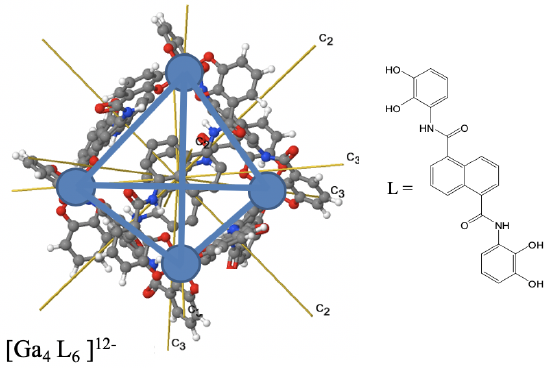
An example is the depicted Ga4L6 cage (Fig. 2.2.16). The Ga atoms occupy the vertices of a tetrahedron, but the point group is not Td but T because of the shape of the ligands that connect the four Ga atoms.
The Octahedral Point Group Oh
Another high symmetry point group is the point group Oh. Both the octahedron as well as the cube belong to this point group despite their very different shape (Fig. 2.2.18). Because they belong to the same point group they must have the same symmetry elements and operations. There are many octahedrally shaped molecules, such as the SF6.
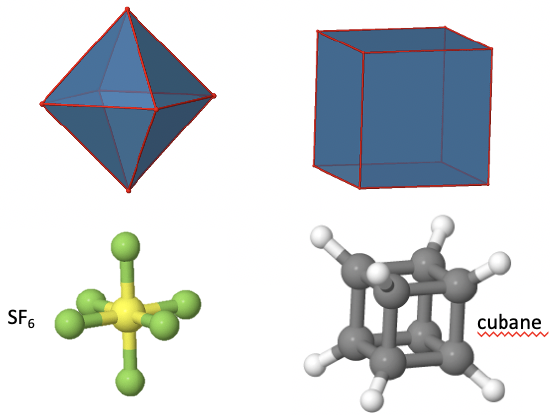
Molecules with cubic shapes are far less common, because a cubic shape often leads to significant strain in the molecule. An example is cubane C8H8. Let us determine the symmetry elements and operations for the point group Oh using the example of the octahedron. If we used the cube, we would get exactly the same results.
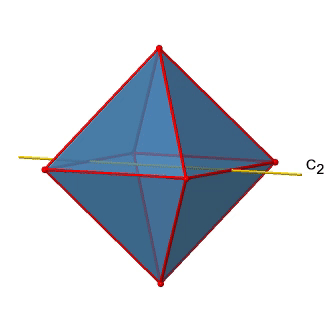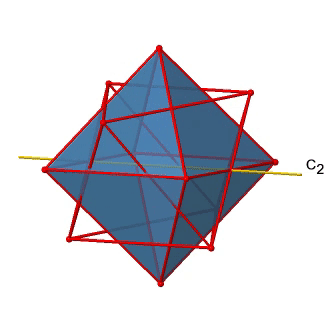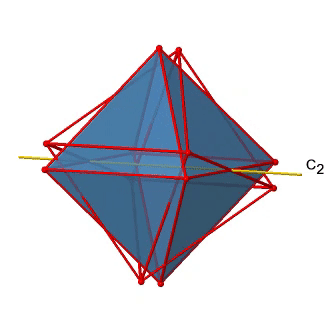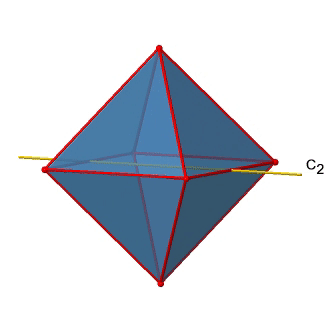
There are three C4 principal axes in the octahedron. They go through two opposite vertices of the octahedron (Fig. 2.2.19). There are three C4 axes because an octahedron has six vertices which are all symmetry-equivalent because the octahedron is a platonic solid.
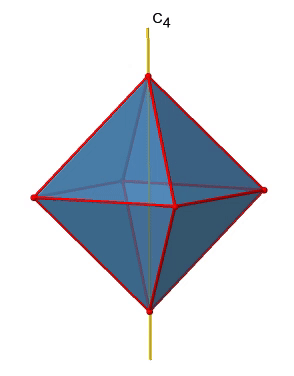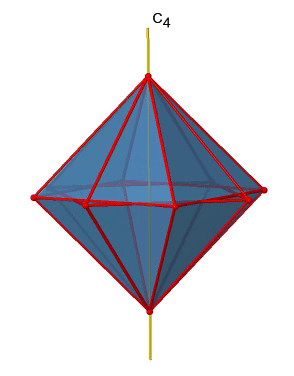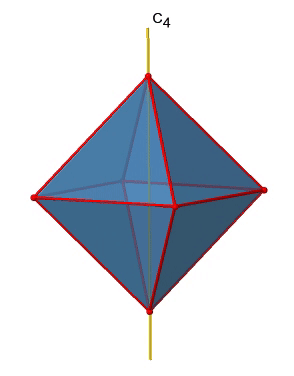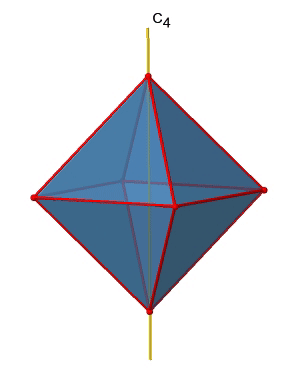
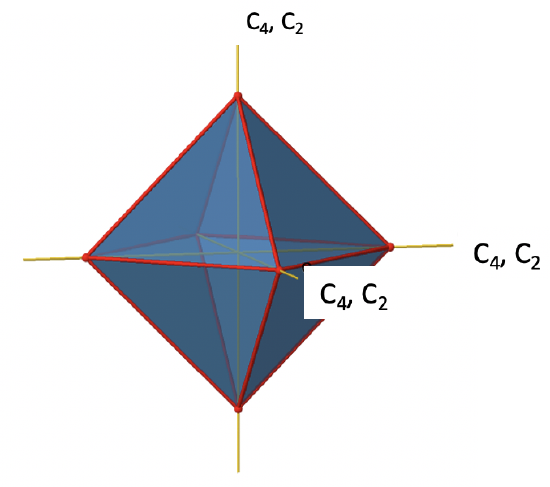
We can see that there are also C2 axes where the C4 axes run. This is because rotating two times around 90° is the same as rotating around 180°. What are the symmetry operations associated with these symmetry elements? Rotating four times around 90° using the C4 axes produces the identity. So we have to consider the operations C41, C42, C43 and C44. How many of these are unique? C44 is the same as the identity, so it is not unique, In addition a C42 is identical to a C21, and thus C42 is also not unique, and can be expressed by the simpler operation C21. That leaves the C41 and the C43 as the only unique symmetry operations. Because we have three C4 axes, there are 2x3=6 C4 operations, in detail there are 3C41 and three C43 operations. In addition, there are the three C21 operations belonging the the three C2 axes (Fig. 2.2.20).

In addition, there are four C3 axes (Fig. 2.2.21). They are going through the center of two opposite triangular faces of the octahedron.
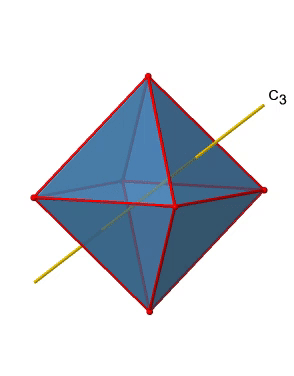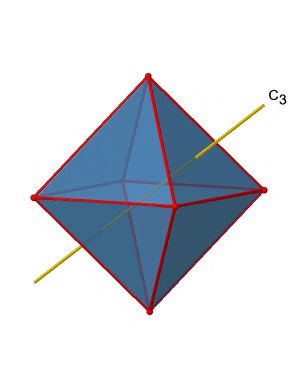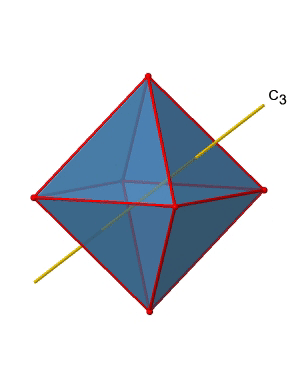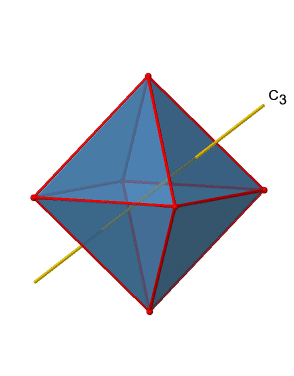
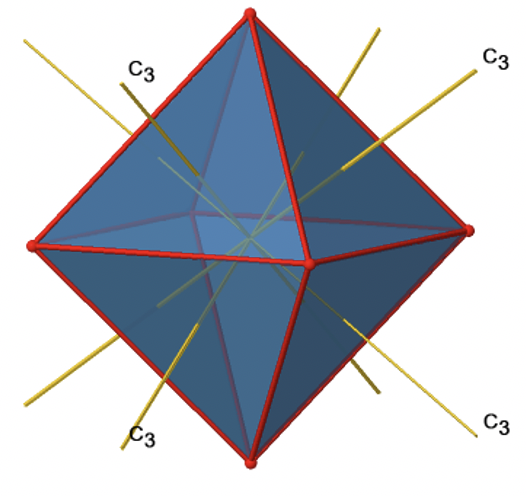
You see above a single C3 axis, and on the right hand side all four of these axes. How can we understand that there are four axes? An octahedron has overall eight triangular faces, and each C3 axis goes through two opposite faces, so there are 8/2=4 C3 axes. Each C3 axis has the C31 and the C32 as unique symmetry operations. The C33 is the same as the identity. So overall we have 4x2=8 operations, four of them are C31, and four of them are C32 (Fig. 2.2.22).

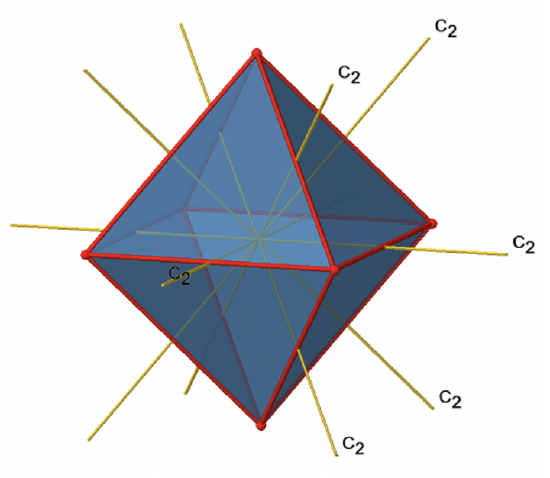
In addition to the C2 axes that superimpose the C4 axes, there are C2’ axes which go though two opposite edges of the octahedron (Fig. 2.2.23). How many of them are there? An octahedron has twelve edges, and because each C2’ passes through two edges, there must be 12/2=6 C2’ axes. These axes have primes because they are not conjugate to the C2 axes that superimpose the C4 axes. For each C2’ axis there is only the C2’ 1 as the unique symmetry operation, and therefore there are overall 6 C2’1 symmetry operations (Fig. 2.2.24).

Let us look at the mirror planes next (Fig. 2.2.25). There are horizontal mirror planes that stand perpendicular to the C4 principle axes. You can see a single one of them below on the left.
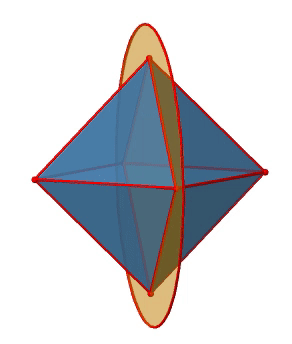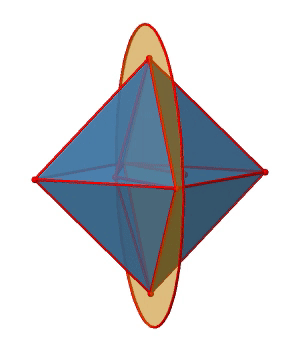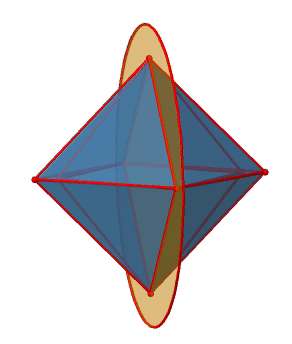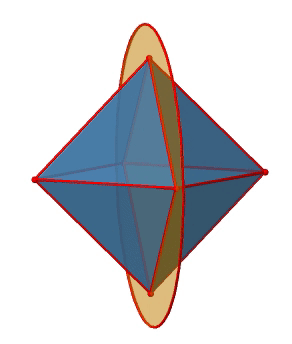
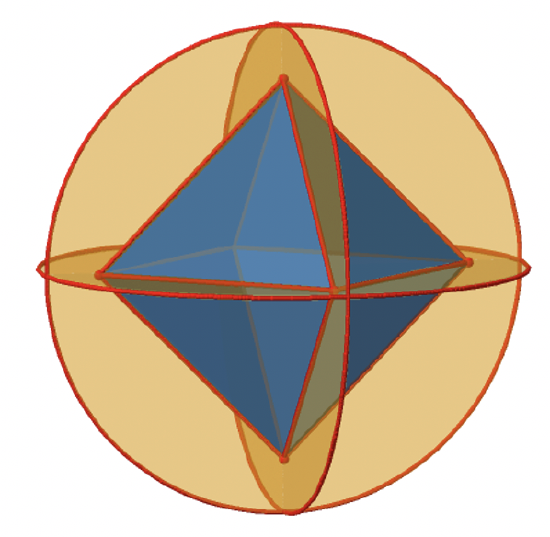
Note that this mirror plane also contains two axes, in addition to the one to which it stands perpendicular. Because it contains two principal C4 axes, it has also properties of a vertical mirror plane. Nonetheless, we call it a horizontal mirror plane because it stands perpendicular to the third C4. The horizontal properties trump the vertical ones, so to say. You can see that a single mirror plane contains four edges of the octahedron. Because there are twelve edges, there are 12/4=3 horizontal mirror planes. There is one mirror plane per principal C4 axis. There are three horizontal reflection operations because there is always only one reflection operation per mirror plane (Fig. 2.2.26).
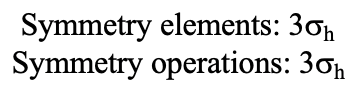
Next let us look for vertical mirror planes (Fig. 2.2.27). A vertical mirror plane is depicted below on the left.
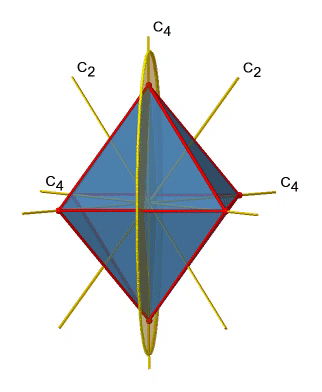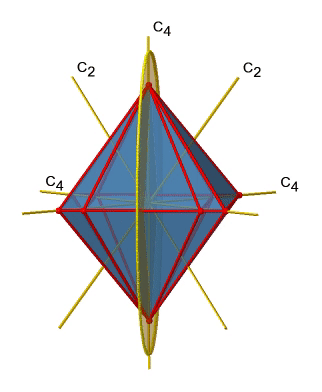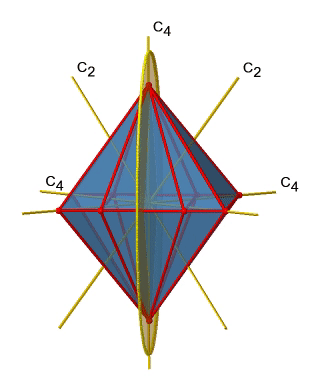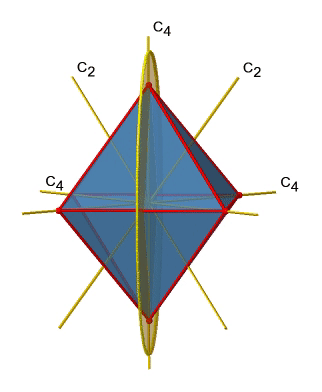
You can see that - contrast to the horizontal mirror planes - it does not contain any edges. Rather, it cuts through two opposite edges. You can see that this plane contains a C4 axis, but it does not stand perpendicular to the other two C4 axes. Therefore it has only the properties of a vertical mirror plane. You can see however, that the mirror plane bisects the angle between two C2’ axes which also depicted. This makes the vertical mirror planes dihedral mirror planes, σd. How may of them do we have? As previously mentioned, each mirror plane cuts through two opposite edges. There are twelve edges in an octahedron, and thus there are 12/2=6 dihedral mirror planes. You can see all of them on the right side of Fig. 2.2.27. Each mirror plane is associated with one reflection operation, therefore there are six dihedral reflection operations (Fig. 2.2.28).

Next we can ask if the point group Oh has an inversion center? Yes, there is one in the center of the octahedron (Fig. 2.2.29)!
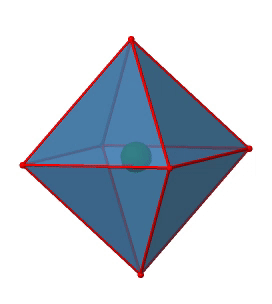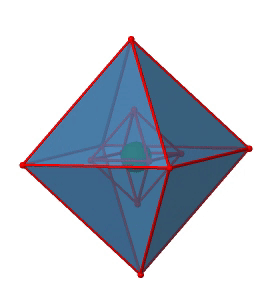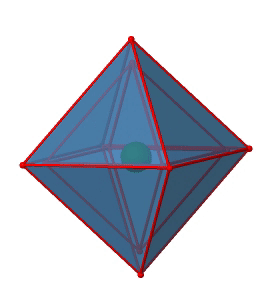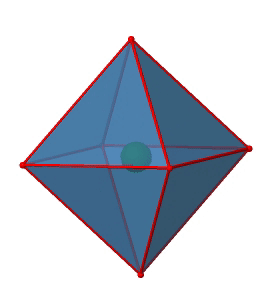
Figure 2.2.29 The inversion center of the octahedral point group Oh (Attribution: symotter.org/gallery)
Each point in the octahedreon can be moved through the inversion center to the other side, and the produced octahedron will superimpose the original one. There is always one inversion operation associated with an inversion center (Fig. 2.2.30).

Next, let us look for rotation-reflections. You can see an S6 rotation-reflection operation below (Fig. 2.2.31, left).
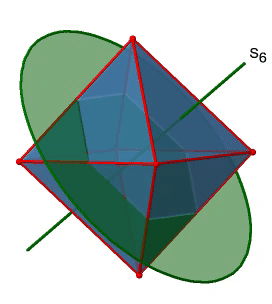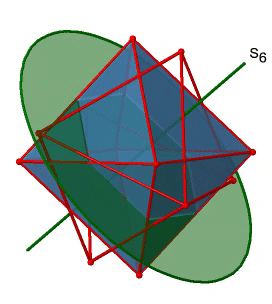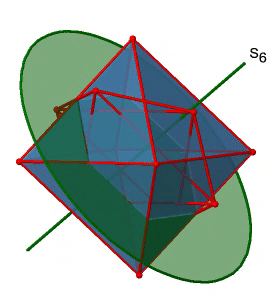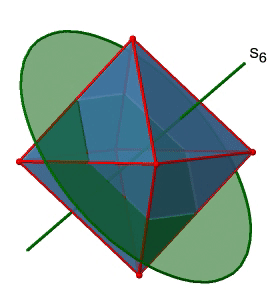

The improper S6 axis passes though the centers of two opposite triangular faces. One can see that rotation about 60° alone does not make the octahedron superimpose. The reflection at a plane perpendicular to the improper axis is required to achieve superposition. Overall, the rotation-reflection swaps up the position of the two opposite triangular faces. How many S6 improper axes are there? Since each S6 passes through two faces, and an octahedron has 8 faces there must be 8/2=4 S4 axes. You can see all of them above (Fig. 2.2.31, right). Note that they are in the same position as the 4C3 axes we previously discussed. How many unique operations are associated with them? For an S6 axis we need to consider operations from S61 to S66. S66 is the same as the identity so it is not unique. The S62 is the same as a C31 because rotating two times round 60° is the same as rotating around 120°, and reflecting twice is the same as not reflecting at all. Similarly, an S64 is the same as an C32. Rotating four time by 60° is the same as rotating two times by 120° and reflecting four times is the same as not reflecting at all. Further, an S63 is the same as an inversion. After three 60° rotations we have rotated by 180°. If we reflect after that, then this is the same as an S21 operation which is the same as an inversion. Therefore, only the S61 and the S65 operations are unique, all other operations can be expressed by simpler operations (Fig. 2.2.32).

The octahedron also has S4 improper axes, and you can see one of them below (Fig. 2.2.33, right).
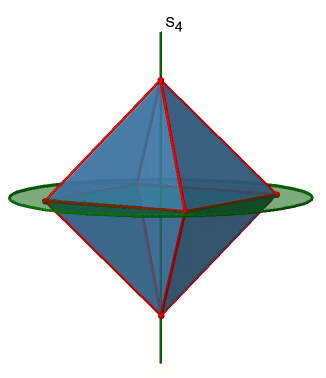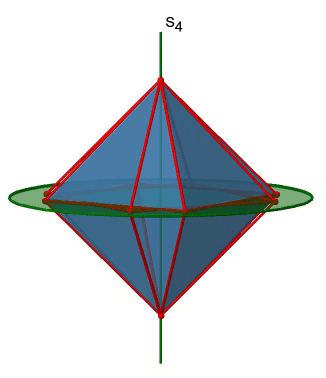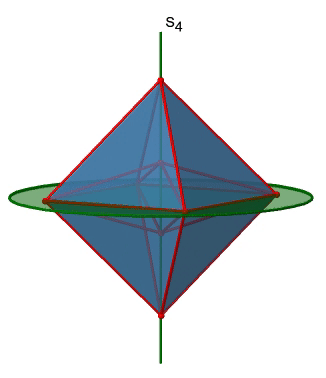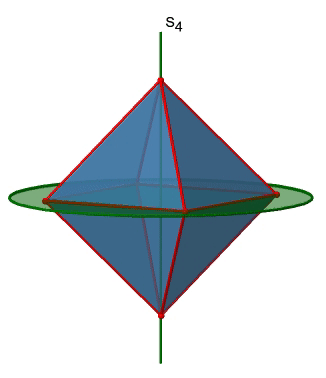
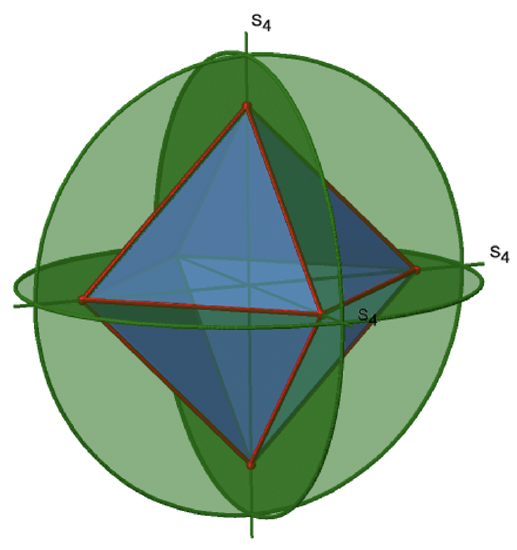
It goes through two opposite corners of the octahedron. The S4 improper axis seemingly does the same as the C4 axis that goes through the same two opposite vertices, but actually does not. While rotating around 90° already makes the octahedron superimpose with its original form, executing the reflection operation after the rotation swaps up the position of the two vertices, and generally all points of the octahedron above and below the plane, respectively. Overall the S4 moves the points within the object differently compared to the C4 which makes it an additional, unique symmetry element. There are overall three S4 improper axes because the octahedron has six vertices and one S4 passes through two vertices (Fig. 2.2.34).

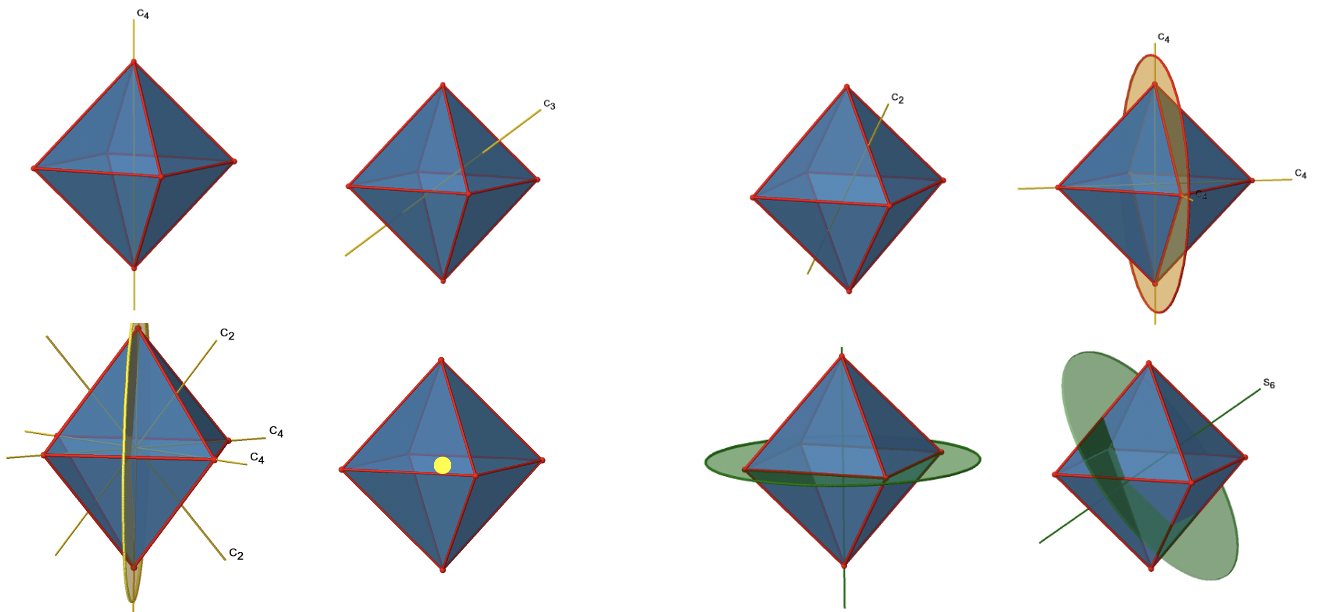
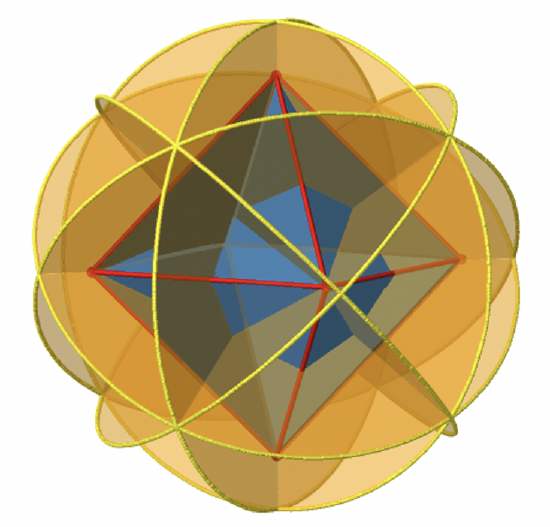
Here is an overview over all the symmetry elements and operations (Fig. 2.2.35 and 2.2.36). Overall, there are 48 different unique operations that one can perform!
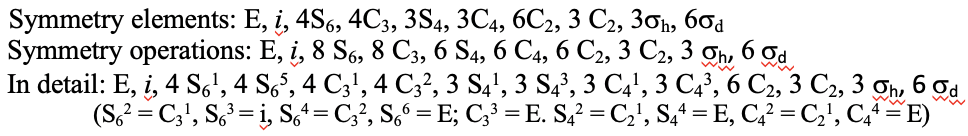
Like the point group Td , also the point group Oh has a rotational subgroup, named O. It has the identity and the same proper rotations as the point group Oh, but no other symmetry operations (Fig. 2.2.38). An example is the polyoxometalate cluster core shown below (Fig. 2.2.37). Polyoxometalates are cluster anions of the group 5 and 6 elements.

Figure 2.2.37 Proper rotations in a V6P8O24 polyoxometalate cluster core. The C3 rotation is animated. (Attribution: symotter.org/gallery)
The point group O is generally rare.
Another high symmetry point group is the point group Th. It can also be derived from the point group Oh. In this case the S4, the C4, the C2’, and the σd operations are removed from the octahedral symmetry. An example is the hexapyridyl iron (2+) cation (Fig. 2.2.39).
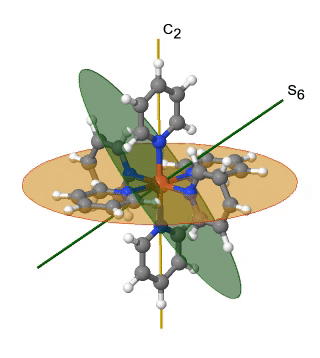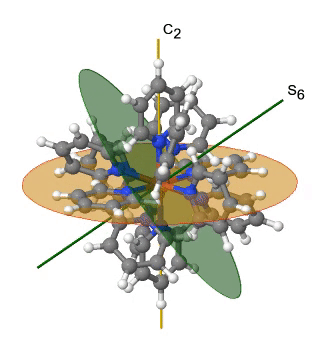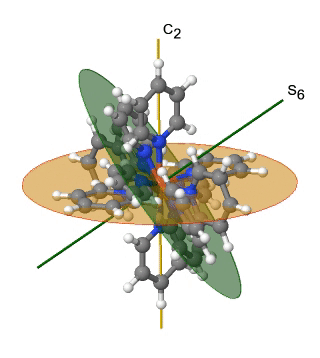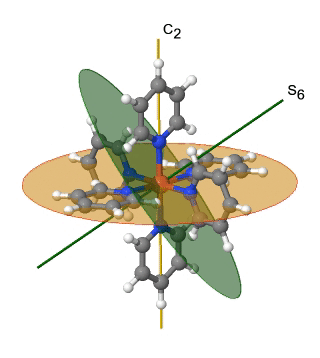
Figure 2.2.39 The hexapyridyl iron (2+) cation and its S6 and C2 symmetry elements. An S6 operation is animated.
You can see that the N-atoms of the pyridyl-ligands surround the Fe atoms octahedrally, but the symmetry is reduced from Oh to Th because of the planar shape of the pyridyl-ligands. In particular the C4 symmetry is reduced to C2. This reduction in symmetry leads to elimination of the S4, the C2’, and the σd symmetry elements (Fig. 2.2.40).

The Ih Point Group
The two remaining platonic solids, the icosahedron and the dodecahedron, belong both to the icosahedral point group Ih. This is despite they are made of different polygons (Fig. 2.2.41).
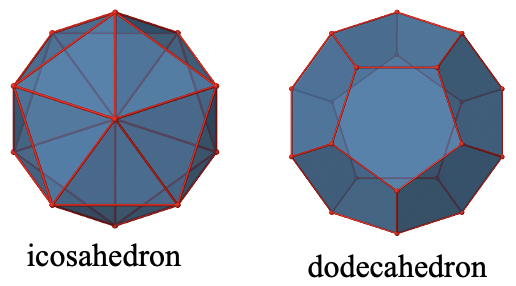
Because they belong to the same point group, they have exactly the same symmetry operations. An example for a molecule with icosahedral shape is the molecular anion B12H122-. An example for a molecule with dodecahedral shape is the dodecahedrane C20H20.
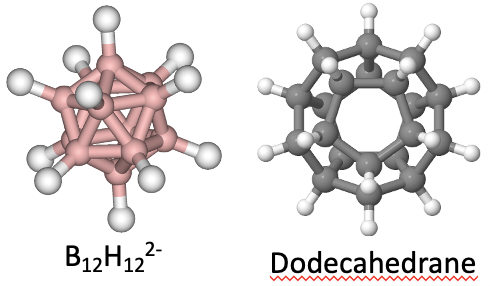
Let us determine the symmetry elements and symmetry operations for the example of the icosahedron. We could also use the dodecahedron, and the results would be the same. The principal axes of the icosahedron are the C5 axes. You can see one of them, going through the center of the pnetagon comprised of five triangular faces below (Fig. 2.2.43).

Figure 2.2.43 One of the C5 axes of the icosahedron stands perpendicular to the paper plane going through the center of a pentagon of the icosahedron (Attribution: symotter.org/gallery)
You can understand that there is a C5 when considering that there are five triangular faces making a pentagon. The C5 axis sits in the center of the pentagon. We can see that when we rotate around this C5 axis, then the produced icosahedron superimposes the original one. The C5 axis goes through two opposite vertices of the icosahedron. Because an isosahedron has 12 vertices, there must be six C5 axes overall. You can see all of them below (Fig. 2.2.44).
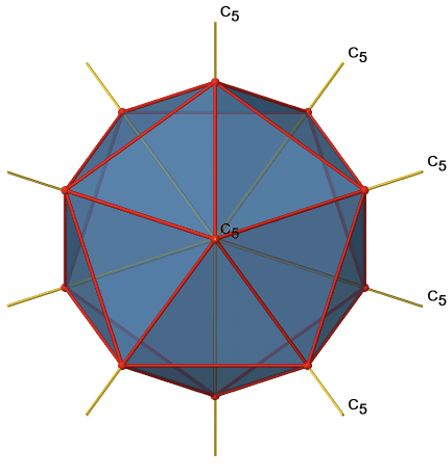
There are four unique symmetry operations associated with a single C5 axis, namely the C51, the C52, the C53, and the C54. The C55 is the same as the identity. Because there are six C5 axes, there are overall 6x4=24 C5 symmetry operations (Fig. 2.2.45).

In addition, there are C3 axes. One of them is shown below, and you can see that it passes through the centers of two opposite triangular faces (Fig. 2.2.46).
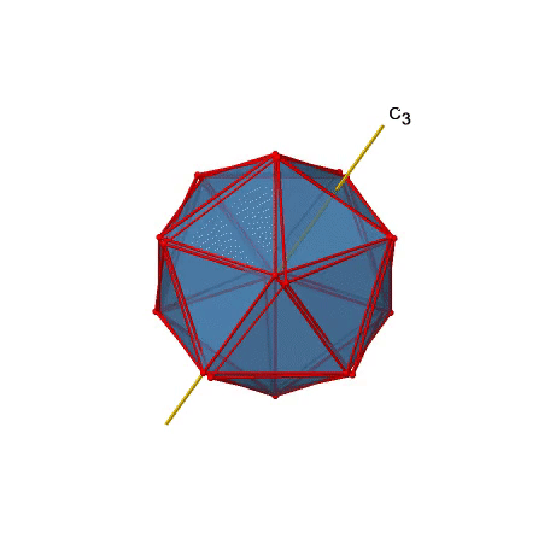
As one rotates by 120° the atoms on the triangular faces change their position, and the resulting icosahedron superimposes the original one. As the name icosahedron says, there are twenty faces overall.
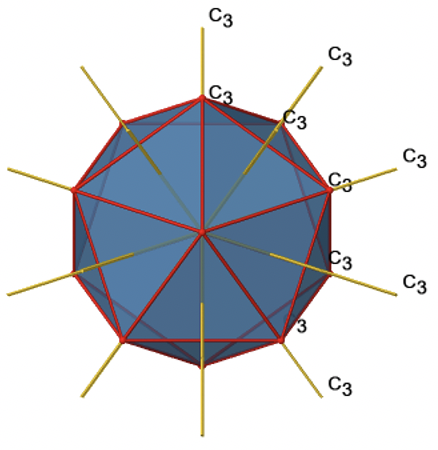
Because one C3 passes through two opposite axes, there are 20/2=10 C3 axes overall (Fig. 2.2.47). Each C3 axis is associated with two symmetry operations, namely C31, and C32. Thus, there are overall 10x2=20 C3 symmetry operations.

There are also C2 axes (Fig. 2.2.49). They pass through the centers of two opposite edges of the icosahedron. Rotating around the C2 axis shown makes the icosahedron superimpose.
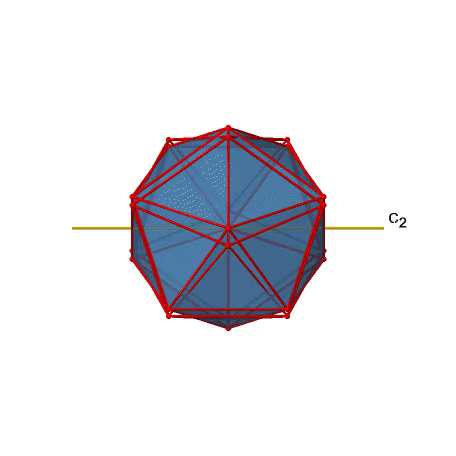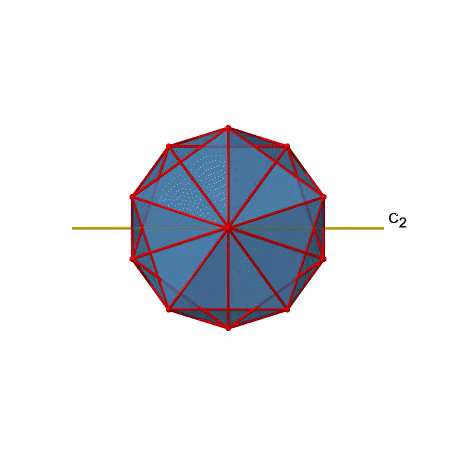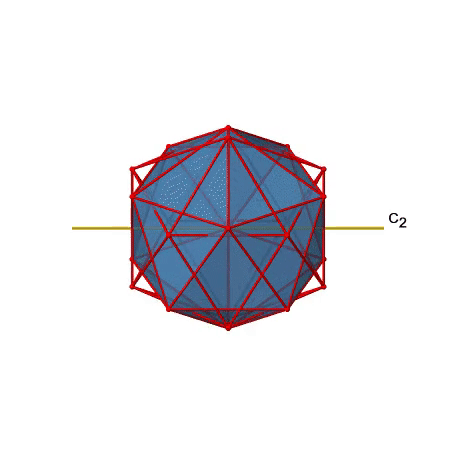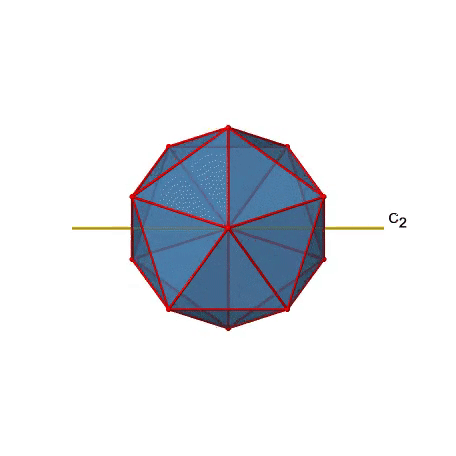
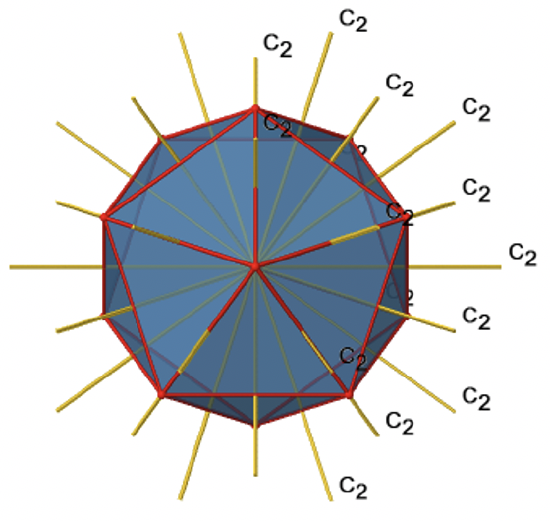
An isosahedron has overall 30 edges. Because one C2 axis passes through the centers of two opposite edges, we can understand that there are 30/2=15 C2 axes. There is one unique C2 operation per axis, and therefore there are 15 C2 operations (Fig. 2.2.50).

We have now found all proper rotations. Let us look for mirror planes, next. You can see a mirror plane below (Fig. 2.2.51).

Figure 2.2.51 A mirror plane in the icosahedral point group (Attribution: symotter.org/gallery)
It contains two opposite edges. It also bisects two other edges. An icosahedron has overall 30 edges, therefore there are 30/2=15 mirror planes. You can see all of them below (Fig. 2.2.52 and Fig. 2.2.53)).

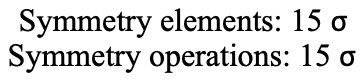
The icosahedron also has an inversion center in the center of the icosahedron (Fig. 2.2.54 and Fig. 2.2.55)).

Figure 2.2.54 The inversion center in the icosahedron (Attribution: symotter.org/gallery)
As we carry out the associated, one symmetry operation, all points in the isosahedron move through the inversion center to the other side.

Let us now look for improper rotations. The improper rotational axes with the highest order are S10 axes. They are located in the same position as the C5 axes, and go through two opposite corners (Fig. 2.2.56).
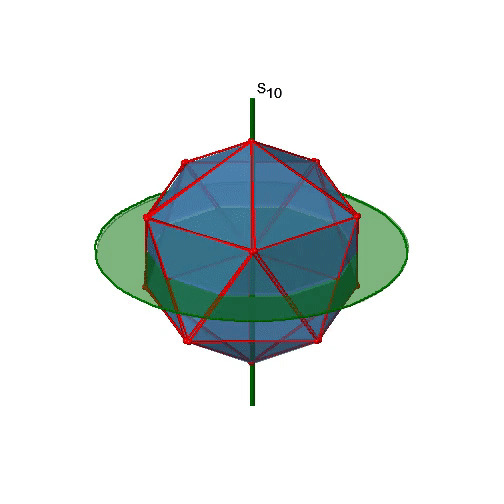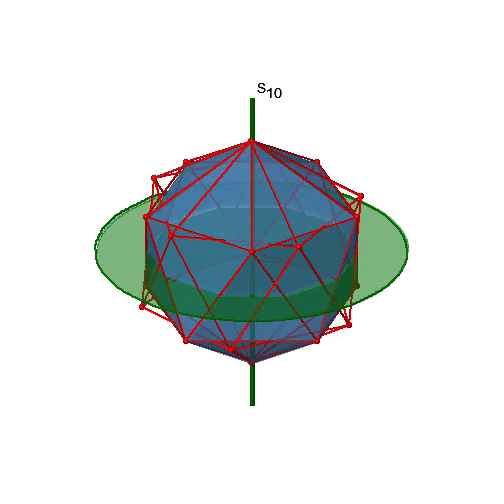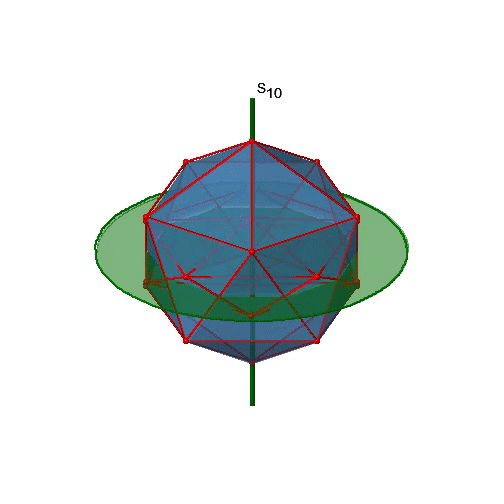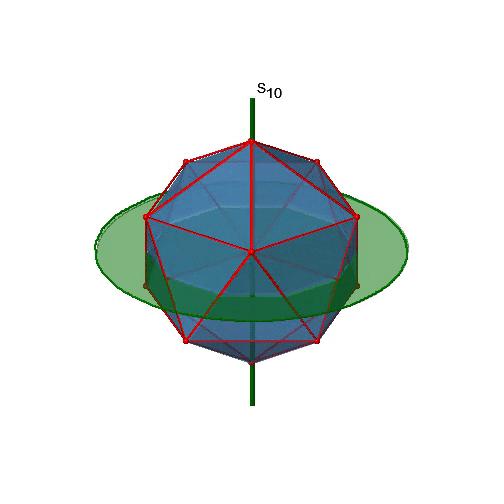
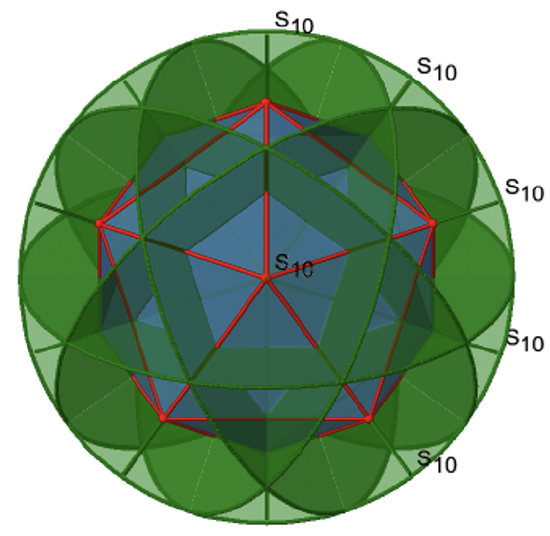
The S10 exists because in an icosahedron there are pairs of co-planar pentagons that are oriented staggered relative to each other. The rotation around 36° brings one pentagon in eclipsed position relative to the other, but superposition is only achieved after the reflection at the mirror plane perpendicular to the rotational axis. Because one S10 passes through two opposite vertices, and there are 12 vertices there are 6 S10 improper axes. For each axis there are four unique symmetry operations, the S101, the S103, the S107, and the S109. Therefore, there are overall 4x6=24 operations possible (Fig. 2.2.57).
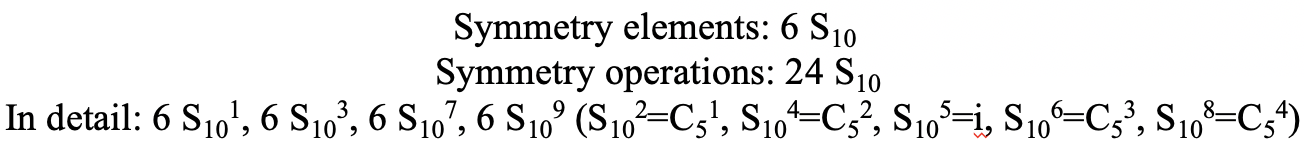
Are the lower order improper rotational axes? Yes, there are S6 axes that pass through the centers of two opposite triangular faces (Fig. 2.2.58). This symmetry element exists because the two triangular faces are in staggered orientation to each other. Rotation alone brings one face in eclipsed orientation relative to the other, but reflection at a mirror plane perpendicular to the axis is required to achieve superposition. The S6 axes are in the same location as the C3 axes.
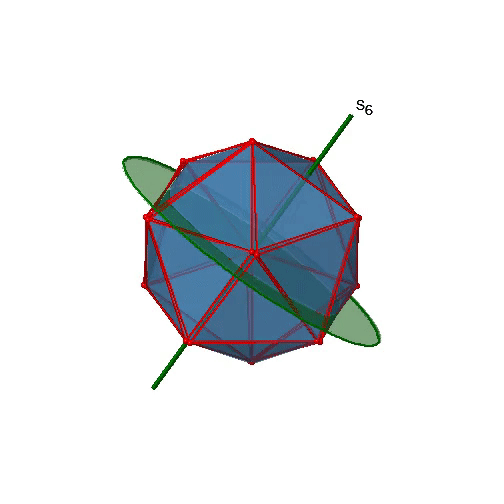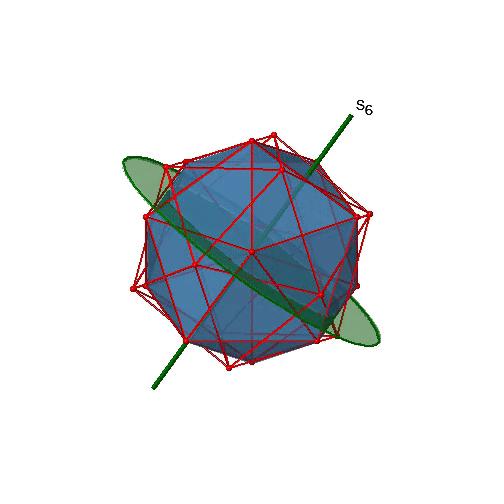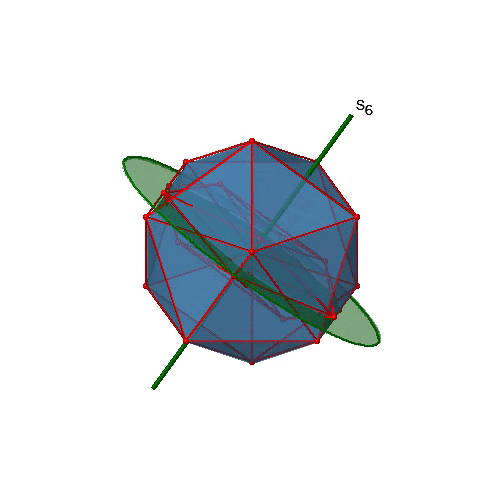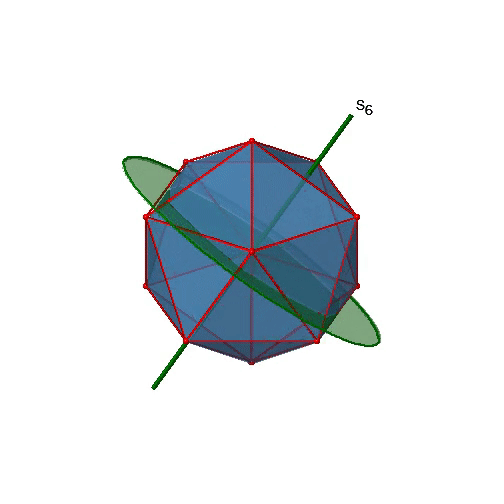
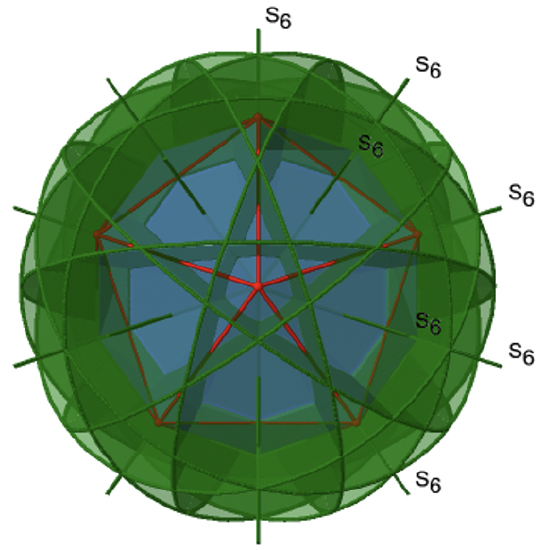
There are 10 S6 axes because there are twenty faces and one axis passes through two opposite faces. Only the S61 and the S65 operations are unique S6 operations, all others can be expressed by simpler operations. Therefore there are overall 10 S61+10 S65 = 20 S6 operations (Fig. 2.2.59).

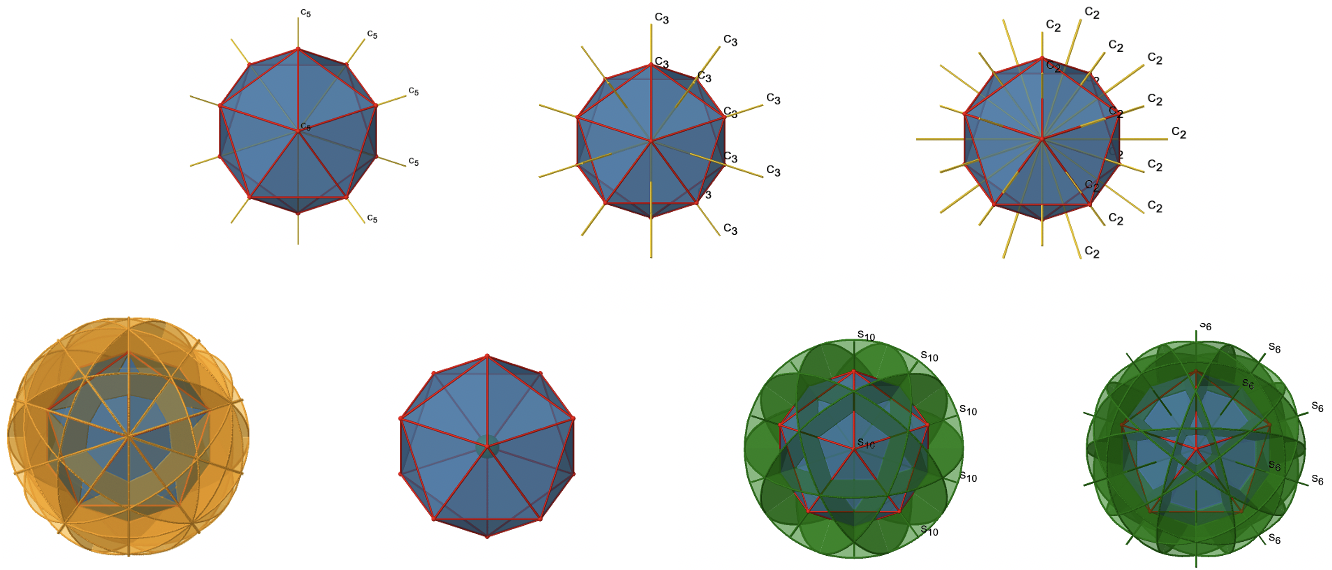
We have now found all symmetry operations for the Ih symmetry. There are overall 120 operations making the point group Ih the point group with the highest symmetry (Fig. 2.2.60 and Fig. 2.2.61).
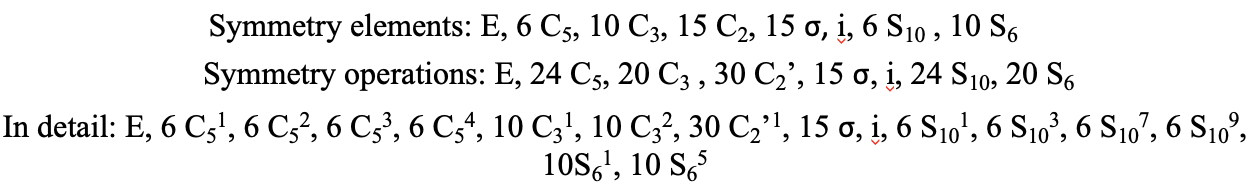
Also the point group Ih has a rotational subgroup.
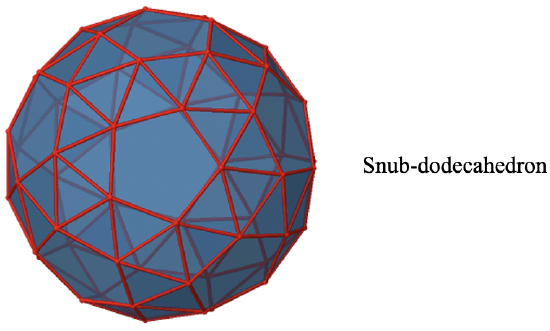
It is called I. An example of an object with this symmetry is the snub-dodecahedron (Fig. 2.2.62). It has the identity, and all the proper rotation operations of the point group Oh, but the inversion, the rotation-reflections, and the mirror planes are eliminated (Fig. 2.2.63).
Cyclic Point Groups
After having discussed high and low symmetry point groups, let us next look at cyclic point groups. They have the property that they have only a single proper n-fold rotational axis, but no other proper axes. In the most simple case they do not have any additional symmetry element such as mirror planes or rotation-reflections. These point groups are denoted Cn whereby n is the order of the proper axis. An example is the hydrogen peroxide molecule H2O2 (Fig. 2.2.64).

Figure 2.2.64 The C2 rotational axis of hydrogen peroxide
It has a so-called roof-structure due to its non-planarity. One hydrogen atom points toward us, and the other points away from us. This structure is due to the two electron-lone pairs at each sp3-hybridized oxygen atom. These electron-lone pairs consume somewhat more space than the H atoms, and there is electrostatic repulsion between the electron lone pairs. Therefore, the electron lone pairs at the different oxygen atoms try to achieve the greatest distance from each other. This forces the H-atoms out of the plane, leading to the roof-structure of the hydrogen peroxide. Because the H2O2 molecule is not planar, it only has a single C2 axis, but no other symmetry element besides the identity. The C2 axis passes through the center of the O-O bond. Execution of the C2 operation swaps up both the O and the H atoms.
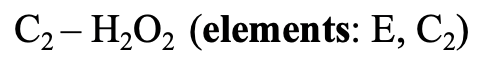
Definition: Cyclic Groups Cn
Cyclic groups have one rotational axiPyramidal Groups
Another class of groups are the pyramidal groups, denoted Cnv. They have n vertical mirror planes containing the principal axis Cn in addition to the principal axis Cn. Generally molecules belonging to pyramidal groups are derived from an n-gonal pyramid. An n-gonal pyramid has an n-gonal polygon as the basis which is capped (Fig. 2.2.66).
For example a trigonal pyramid has a triangular basis which is capped, a tetragonal pyramid has a square which is capped, and so on. The proper axis associated with a specific pyramid has the order n and goes through the tip of the pyramid and the center of the polygon. An example of a molecule with a trigonal pyramidal shape is the NH3 (Fig. 2.2.67).

The three H atoms form the triangular basis of the pyramid, which is capped by the N atom. The NH3 molecule belongs to the point group C3v. The C3 axis goes though the N atom which is the tip of the pyramid, and the center of the triangle defined by the H atoms. There are three vertical mirror planes that contain the C3 axis. Each of them goes through an N-H bond (Fig. 2.2.68).

Definition: Pyramidal Groups Cnv
Pyramidal groups have n vertical plane(s) in addition to the principal axis Cn.
The Linear Group C∞v
A special n-gonal polygon is the cone. A cone can be conceived as an n-gonal pyramid with an infinite number n of corners at the base (Fig. 2.2.69).
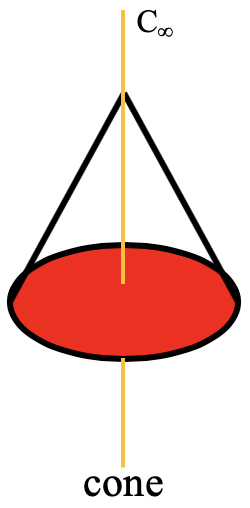
In this case the order of the rotational axis that passes through the tip of the cone and the center of the circular basis is infinite. This also means that there is an infinite number of vertical mirror planes that contain the C∞ axis (Fig. 2.2.71). The point group describing the symmetry of a cone is called the linear point group C∞v. Polar, linear molecules such as CO, HF, N2O, and HCN belong to this point group. You can see the HCN molecule with its C∞ axis and its infinite number of vertical mirror planes below (Fig. 2.2.70).
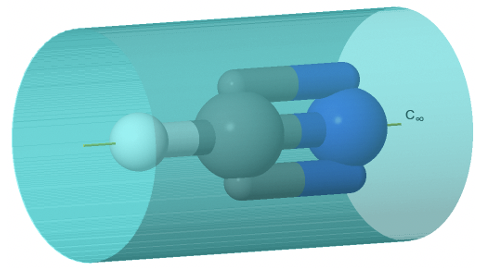
The infinite number of mirror planes, shown in blue are forming a cylinder that surround the molecule.
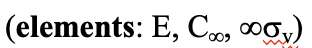
Definition: Linear group Coov
The linear group C∞v has an infinite number of vertical mirror planes containing a C∞ axis
Reflection Groups
If we add a horizontal mirror plane instead of n vertical mirror planes to a proper rotational axis Cn we arrive at a the reflection point group type Cnh. The presence of the horizontal mirror planes also generates an improper axis of the order n. This is because when one can rotate and reflect perpendicular to the rotational axes independently, then it must also be possible to do it in combination. An example of a molecule belong to a reflection group is the trans-difluorodiazene N2F2 (Fig. 2.2.72).
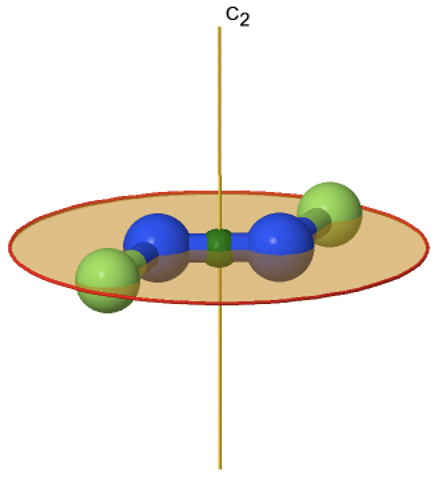
It is a planar molecule with a C2 axis going through the middle of the N-N double bond, and standing perpendicular to the plane of the molecule. The horizontal mirror plane stands perpendicular to the C2 axis, and is within the plane of the molecule. There is an additional inversion center because an S2 must exist which is the same as an inversion center. The inversion center is in the middle of the N-N bonds. Overall, the molecule has the symmetry C2h.

Definition: Reflection Group Cnh
A reflection group has a horizontal plane perpendicular to the principal axis Cn
Dihedral Groups
Dihedral groups are point groups that have n additional C2 axes that stand perpendicular to the principal axis of the order n. If there are no other symmetry elements, then the point group is of the type Dn.
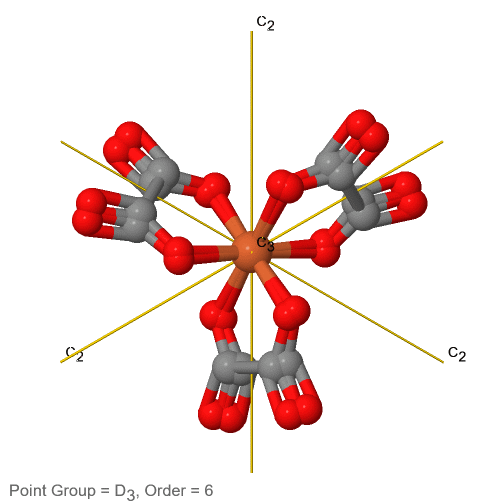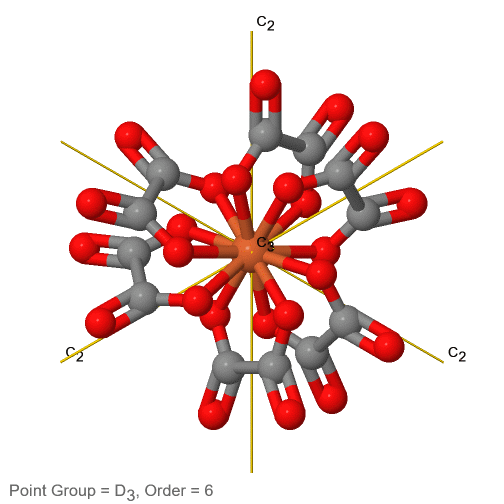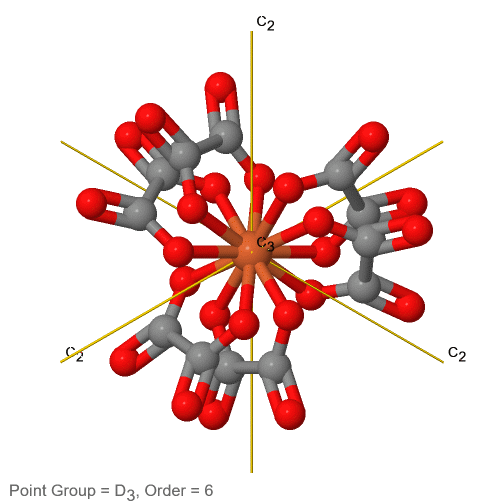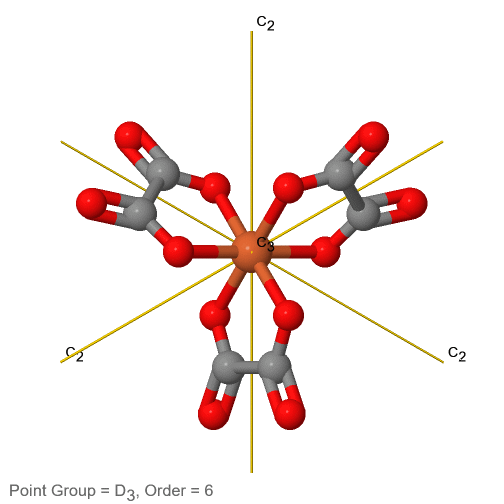3_C3.gif?revision=1)
Figure 2.2.74 The tris-oxolato ferrate (3-) ion and its symmetry elements
For example in the point group D3 there is a C3 principal axis, and three additional C2 axes, but no other symmetry element (Fig. 2.2.75). The tris-oxolato ferrate (3-) ion belongs to this point group (Fig. 2.2.75). You can see that the C3 axis stands perpendicular to the paper plane, and there are three C2 axes in the paper plane.

Definition: Dihedral Groups Dn
In a point group of the type Dn there is a principal axis of order n, n C2 axes, but no other symmetry elements.
If a horizontal mirror plane is added to the Cn axis and the n C2 axes we arrive at the prismatic point groups Dnh (Fig. 2.2.76). The addition of the horizontal mirror plane generates further symmetry elements namely an Sn and n vertical mirror planes.
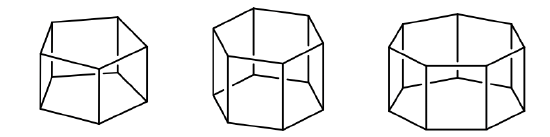
Generally, molecules belonging to this point group derive from n-gonal prisms. The order of the principal axis is the same as the number of corners of the polygons the prism are made of.
Definition: Prismatic Groups Dnh
In prismatic point groups there is a horizontal mirror plane perpendicular to the principal axis Cn. There are also n C2 axes.
An example for a molecule belonging to a prismatic point group is PF5 (Fig. 2.2.77).
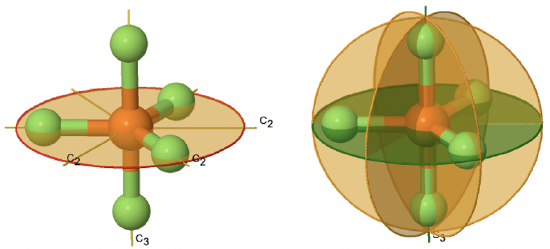
It has a trigonal bipyramidal shape. The C3 axis goes through the axial F atoms of the molecule, and the three C2 axes go through the three equatorial F atom. The horizontal mirror plane stands perpendicular to the principal C3 axis and is located within the equatorial plane of the molecule. In addition, there are the vertical mirror planes that contain the C3 axis, and go through the three equatorial P-F bonds. There is also an S3 axis which superimposes the C3 axis. In sum:
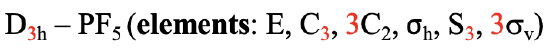
A special case of a Dnh group is the linear group D∞h. An object that has this symmetry is a cylinder. A cylinder can be conceived as a prism with an infinite number of vertices. Thus, the principal axis that passes through a cylinder has infinite order. Because of the infinite order of the principal axis, there is an infinite number of C2 axes that stand perpendicular to the principal axis. You can see one such C2 going though the cylinder (Fig. 2.2.79).
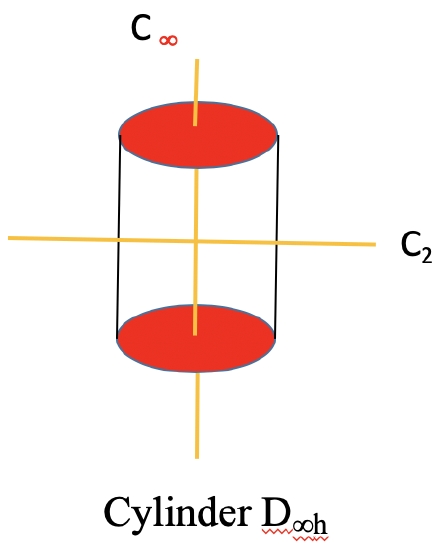
There is now also an improper axis of infinite order, as well as an infinite number of vertical mirror planes. Non-polar linear molecules like H2, CO2, and acetylene C2H2 belong to the point group D∞h. You can see the C∞ axis passing through a CO2 molecule below (Fig. 2.2.80).
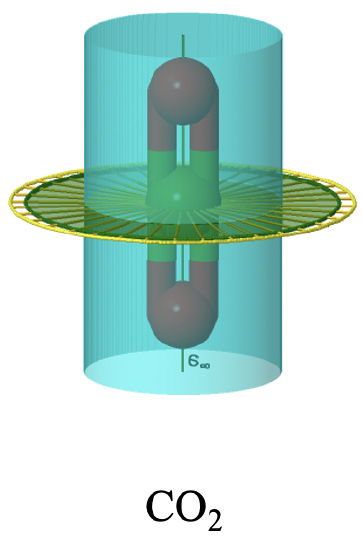
You can see the infinite number of vertical mirror planes as a blue cylinder. The infinite number of C2 axes is shown a yellow lines going around the molecule. In sum:

Definition: Linear Group Dooh
In the point group D∞h there is an infinite number of n C2 axes in addition to the principal axis of infinite order, an infinite number of vertical mirror planes, and one horizontal mirror plane.
If we add n vertical mirror planes to the principal axis and the n C2 axes, we arrive at the point group Dnd. The vertical mirror planes are dihedral mirror planes because they bisect the angle between the C2 axes. An example is the ethane molecule in staggered conformation which has the symmetry D3d (Fig. 2.2.82).
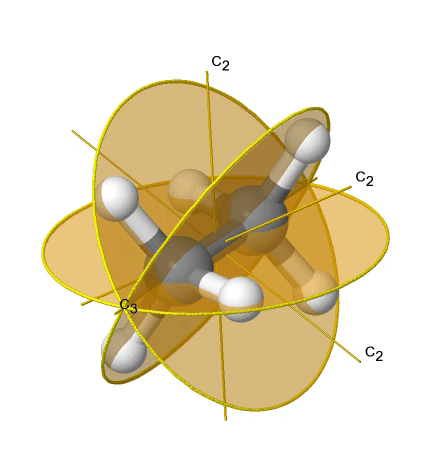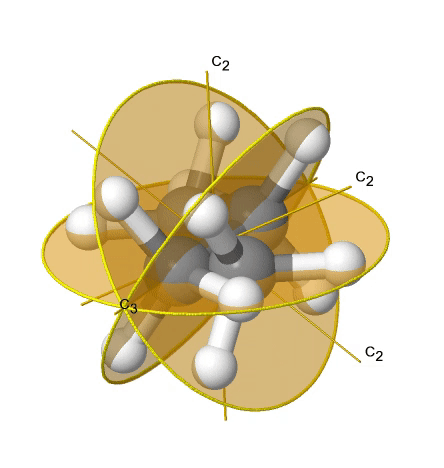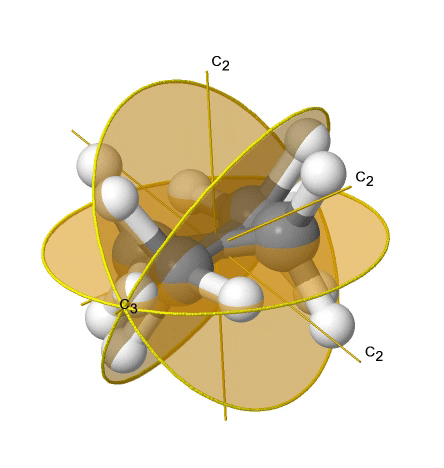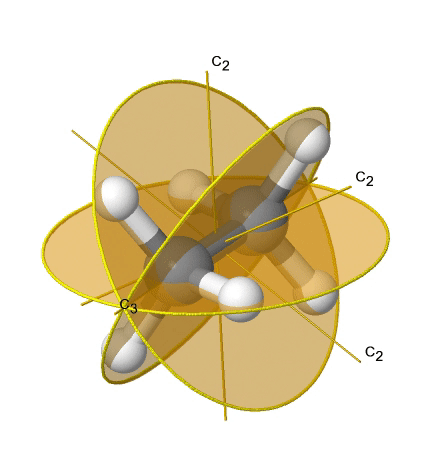
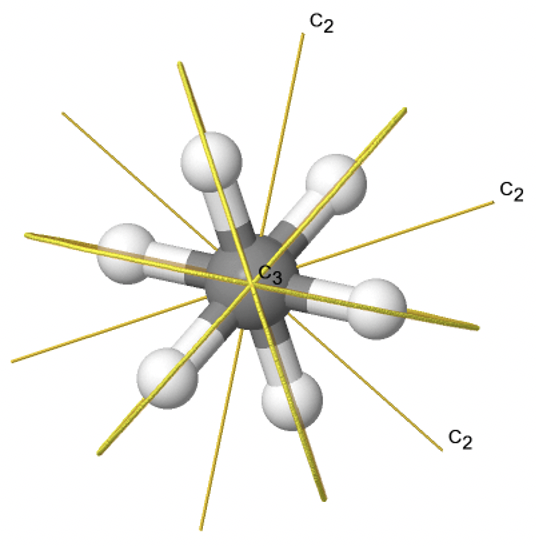
The C3 axis goes along the C-C bond, and the 3C2 axes pass through the middle of the carbon-carbon bond, and bisect the angle between two hydrogens and one carbon atom. The three dihedral mirror planes pass through the C-H bonds. In addition, the ethane molecule has an S6 axis, and an inversion center. In sum:
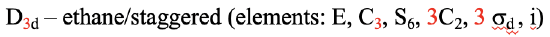
Definition: Dnd
In this point group type there are n dihedral mirror planes that contain the Cn and bisect the angle between adjacent C2 axes
Improper Rotational Point Groups
The last class of point groups to be discussed are the improper rotation point groups. The only have one proper rotational axis, and an improper rotational axis that has twice the order of the proper rotational axis (Fig. 2.2.85). There may be an inversion center present depending on the order of the proper and improper axes. An example the tetramethylcycloocta-tetraene molecule (Fig. 2.2.84).
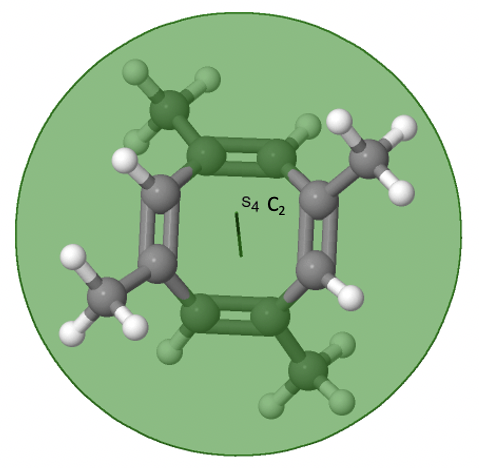
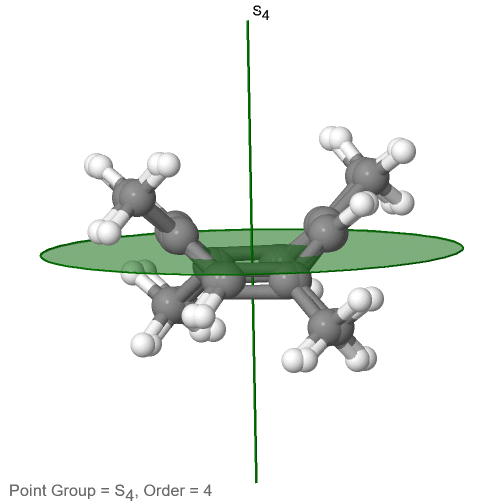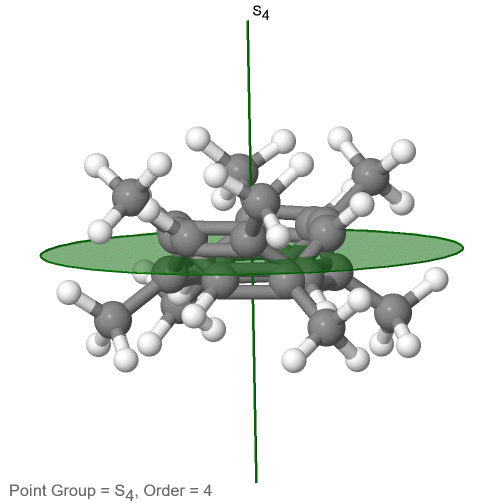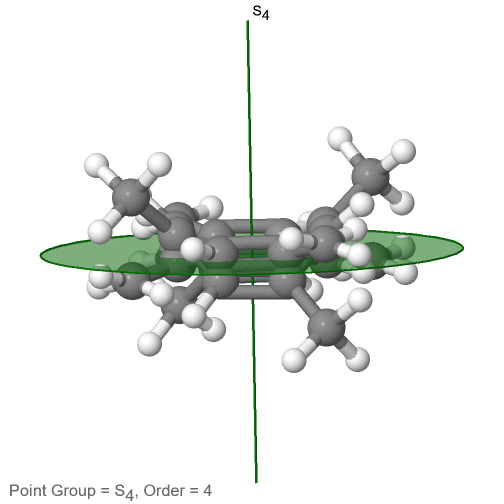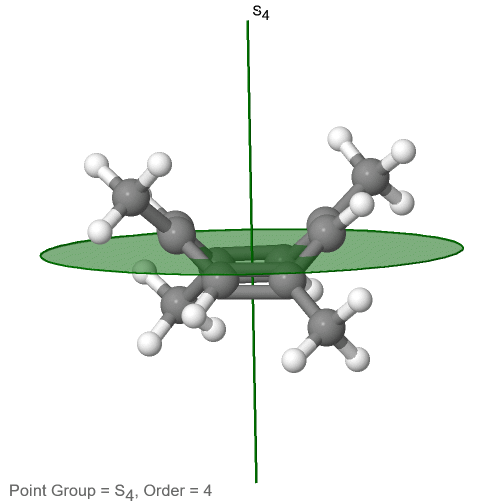
Figure 2.2.84 The S4 and an C2 axes of tetramethyl cycloocta-tetraene
It has an S4 and an C2 axis as the only symmetry elements besides the identity. Rotating by 90° alone does not superimpose the molecule because two C-C double bonds lie above the plane and two below the plane. In addition, two opposite methyl groups lie above and below the plane respectively. Therefore it needs the additional reflection to achieve superposition. There is also a C2 axis which is in the same locations as the S4 axis.

Guide for the Determination of Point Groups
With the knowledge you have, you can unambiguously identify the point group of a molecule. The key to success is that you are able to see the symmetry elements in the molecule. This takes practice. With enough practice you can identify the point group of a molecule immediately. Until, you can use guides, that you can follow to identify a point group. Such a guide asks systematic questions about the presence or absence of a symmetry element. Depending on whether you answer the question with yes or no you can follow the guide in a particular direction. Eventually, after having answered enough questions the guide will lead you to the respective point group. You can see such a chart below (Fig. 2.2.86).
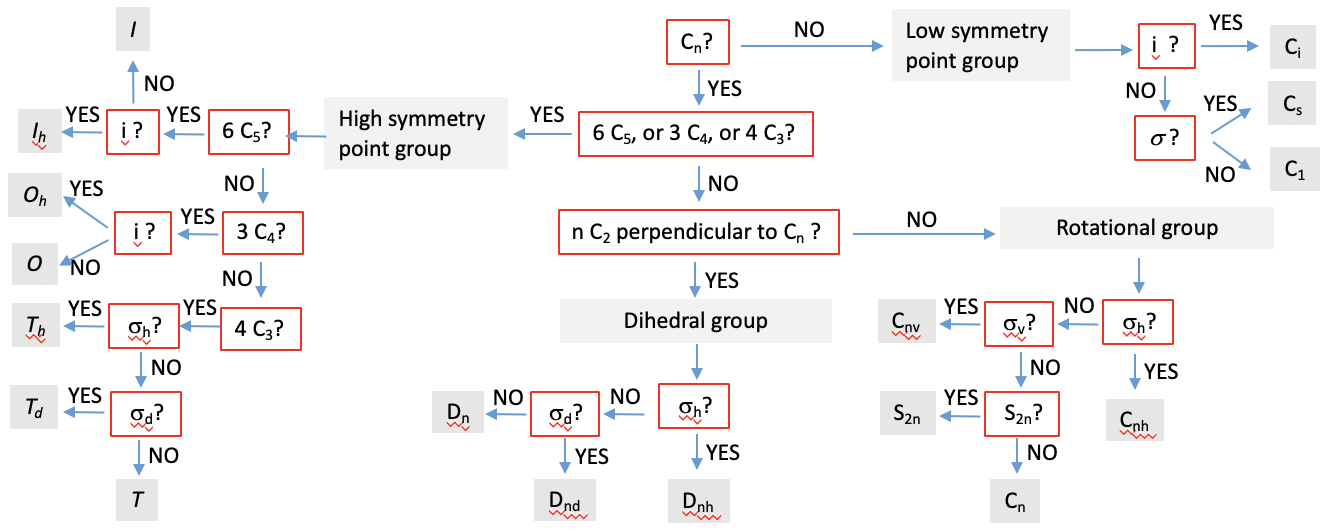
You can first ask if there is at least one Cn present. If not, then the molecule must be in a low symmetry point group. If there is an inversion center, the point group is Ci. If not we can next ask, if there is a mirror plane. If yes it is Cs, and if not the point group is C1. If a low symmetry point group can be ruled out, then we can ask next, if there is a high symmetry point group. This is the case when there are either 4C3, 3C4, or 6C5 rotational axes present, standing for tetrahedral, octahedral, and icosahedral symmetry, respectively. If there is an inversion center in case a C5 is present, the point group is Ih. If not, it is I. Similarly, if there are 3C4 axes, and an inversion center, the point group must be Oh. If there is no inversion center the point group is O. If there are 4C3 axes, the point group must be T type. If there is a horizontal mirror plane in addition, then the point group must be Th. If not, we can ask next is there are dihedral mirror planes. If yes, the point group is Td, otherwise it is T. Now we have checked for all high symmetry point groups.
If a high-symmetry point groups can be ruled out, we ask if there are n C2 axes in addition to the Cn principal axis. If this is so, then we must have a dihedral group of the D type. Next we ask, if there is a horizontal mirror plane. If yes, the point group must be Dnh. If not, we ask if there are dihedral mirror planes. If yes, the point group is Dnd. If there are no mirror planes at all, then the point group is Dn. If there are no n C2 axes in addition to the Cn, the the group must be either a rotational group or an improper rotation group. We next ask, if there is a horizontal mirror plane. If yes, then the point group is of the type Cnh. If not, we ask if there are vertical mirror planes. If yes, then the point group is Cnv. If that is not the case, we ask if there is an S2n in addition to the Cn. If yes, the point group is S2n. If not, it is Cn.
Example: Dibromonaphtalene
Let us practice the point group guide by one example. Let us look at the dibromonaphtalene molecule (Fig. 2.2.87).
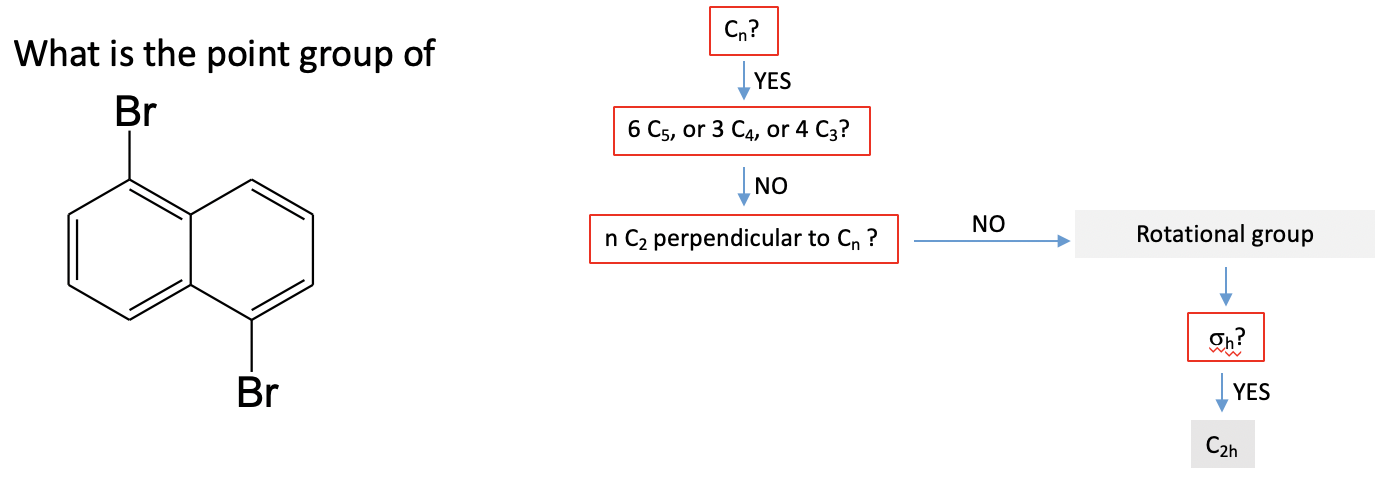
The first question we would ask is: Can you see at least one proper rotational axis? The answer is yes. There is a C2 proper rotational axis that stands perpendicular to the plane of the molecule and goes through the center of the C-C bond that is shared by the two aromatic rings. Next we ask: Are the 6C5, 3C4 or 4C3 axes? That is clearly not the case, and thus we do not have a high symmetry point group. Next we can think about if the there are 2C2 axes in addition to the C2 axes we already found. The answer is no, so the point group cannot be a dihedral group. Next, we would ask: Is there a horizontal mirror plane. This is indeed the case. There is a horizontal mirror plane in the plane of the molecule. It does not move any atoms around, but as we discussed before, a mirror does not need to do this to exist. This identifies the point group as C2h.
Chiral Point Groups
A chiral point group is a point group that only has proper rotation operations in addition to the identity. This is equivalent to the statement that no improper rotations must exist in a chiral point group. This includes mirror planes and inversion centers because a mirror plane is the same as an S1, and an inversion center is the same as an S2. If a molecule belongs to a chiral point group, then it has a mirror image that cannot be superimposed with the original molecule. The two mirror images are called enantiomers. An example is the bromochlorofluoromethane. You can see two enantiomers separated by a dotted line (Fig. 2.2.88).
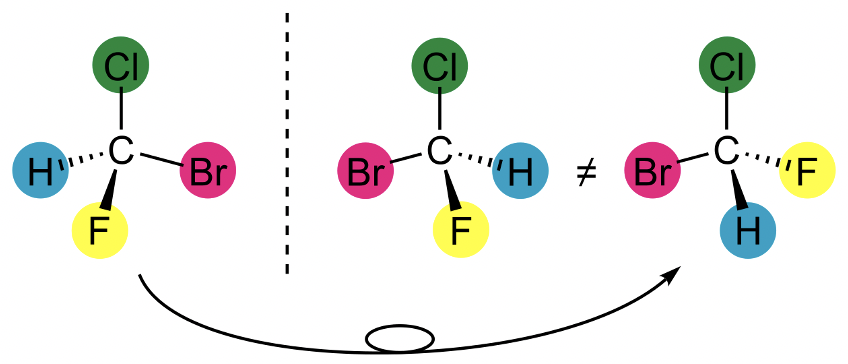
The dotted line represents a mirror plane. Note that this mirror plane is not a mirror plane in the meaning of a symmetry element. You can see that the two molecules to the left and the right of the mirror plane are mirror images respective to each other. The molecules cannot be superimposed meaning that they are enantiomers. Note that the bromochlorofluoromethane molecule on the far right is not an enantiomer to the other two. It the same molecule as the enantiomer on the far left. We only need to rotate clockwise around the C-Cl axis to make the two molecules superimpose meaning that they are the same.
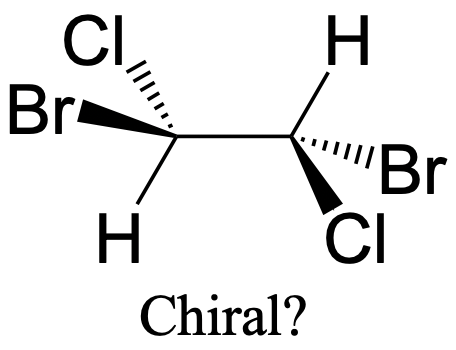
It should be pointed out that the fact that a molecule has a carbon with four different substituents is not sufficient to make it a chiral molecule. The dibromodichloroethane molecule shown above (Fig. 2.2.89) has four different substituents around the carbon atom, but it is not chiral because there is an inversion center in the middle of the C-C bond.
Chiral High Symmetry Point Groups
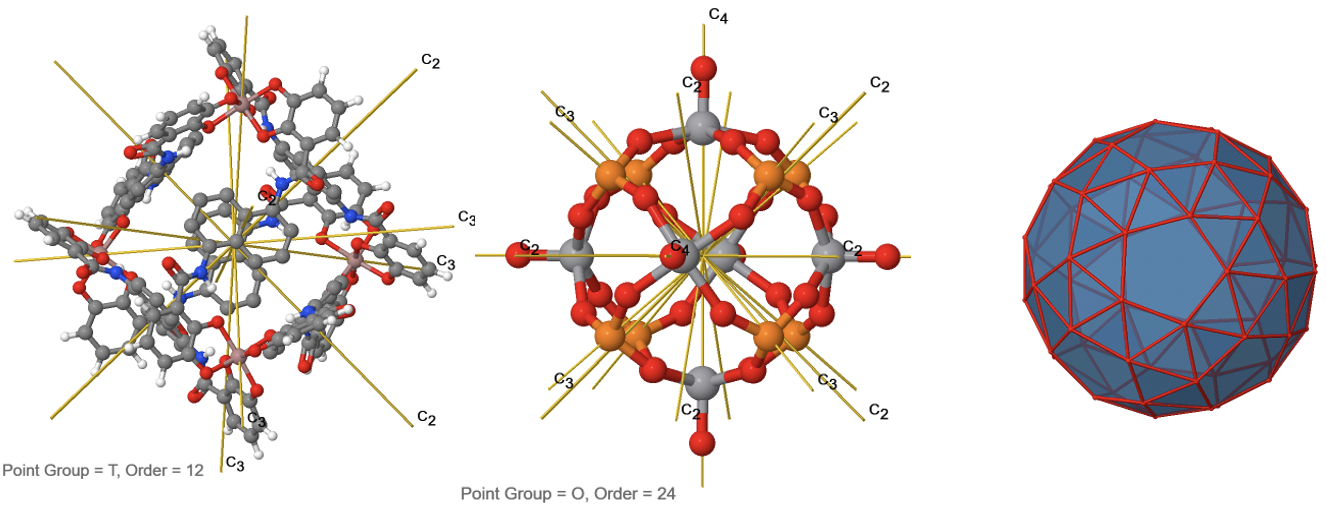
Chiral groups not necessarily need to have low symmetry, in fact, the high symmetry rotational subgroups I, O, and T are chiral groups because they only have proper axes in addition to the identity (Fig. 2.2.90).
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


