1.1: Historical Development of Atomic Theory
- Page ID
- 242481
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Development of Atomic Theory
Since the ancient times, humans thought of explaining the material world in all of its complexity. The basic idea behind all element theories is that the matter that surrounds us is composed of more simple matter. This matter may be composed of even simpler matter. The most simple matter would be called an element.
The first element theories were one element theories: The greek philosopher Thales thought water was the only element, and everything was a form of water. Anaximenes thought air was the only element, and Heraclitus believed fire was the only element (Figure 1.1.1).



However, with only one element assumed it was difficult to explain the material world in all its complexity satisfactorily. This could be done more satisfactorily by a multi-element theory. The first philosopher who introduced a multi-element theory was Empedocles. He suggested a four-element theory with fire, air, water, and soil as the elements (Figure 1.1.2).

First atomistic ideas

The element theories of Thales, Anaximenes, Heraklitus, and Empedocles were all non-atomistic. This means that they did not include the idea that elements were made of small particles that were indivisible. The first greek philosophers that introduced atomistic element theory were Leukippes, and Democrites (Figure 1.1.3). They assumed that particles cannot be divided into smaller particles infinitely often. Ultimately, after many divisions, one would arrive at particles that could not be further divided, and these particles would be called atoms. Atomistic element theory allows for many different elements which helps to explain the complexity of the material world satisfactorily. However, Leukippes and Democrites did not know how many different elements there were, and how different atoms of different elements were actually distinguished. This question would not be answered until about 2000 years later.
Modern Atomic Theories

Although the atomistic idea was already known in the antique, it became forgotten for a long time and was only reintroduced about 2000 years later with Dalton’s atom hypothesis. What lead to Dalton’s atom hypothesis? The first discovery that was important to the development of modern atomic theory was the law of the conservation of mass by Antoine Lavoisier (Fig. 1.1.4). Historically, the conservation of mass and weight was kept obscure for millennia by the buoyant effect of the Earth's atmosphere on the weight of gases, an effect not understood until the vacuum pump first allowed the effective weighing of gases using scales. Until then, in many instances mass seemed to appear or disappear. For example, the mass of wood seems to disappear when it is burned. However, the mass of the wood actually does not disappear it is just converted into the mass of gases, mainly carbon dioxide. When scientists realized that mass never disappeared they could for the first time embark on quantitative studies of the transformations of substances. This in turn led to the idea of chemical elements, as well as the idea that all chemical processes and transformations are simple reactions between these elements. The law of conservation of mass states that the mass of a closed system of substances will remain constant, regardless of the processes acting inside the system. An equivalent statement is that matter cannot be created or destroyed, although it may change form. This implies that for any chemical process in a closed system, the mass of the reactants must equal the mass of the products.
Law of Constant Composition
The discovery of the law of the conservation of mass led to the discovery of the law of the constant composition (also called law of definitive proportions) by Joseph Proust (Fig. 1.1.5). This law was the result of chemical analysis that determined the mass ratio of elements in pure substances. It was found that a pure substance always contains exactly the same proportion of elements by mass. For example the element analysis of pure substances containing the elements carbon and oxygen would be either 42.9% carbon and 57.1% oxygen or 27.3% carbon and 72.7% oxygen.

The law was questioned by Proust's fellow Frenchman Claude Louis Berthollet, who argued that the elements could combine in any proportion. The very existence of this debate was because at the time the distinction between pure chemical compounds and mixtures had not yet been fully developed. When two pure compounds of two different elements are mixed, then the mixture can have a continuous mass ratio between the two elements because compounds can be mixed at any ratio. So, for the example in the two compounds between carbon and oxygen, in mixtures of the two there could be carbon to oxygen ratios varying continuously between 27.7 % to 42.9% carbon, and 42.9% to 72.7% oxygen. It was an accomplishment of Proust that he was able to correctly distinguish between pure compounds and mixtures.
The Law of Multiple Proportions

John Dalton (Fig. 1.1.6) discovered the law of multiple proportions by close analysis of Proust’s law of constant composition. He noticed that if two elements form more than one compound between them, then the ratios of the masses of the second element which combines with a fixed mass of the first element will be the ratios of small whole numbers, also called integer numbers. Let us see what is the meaning of the law of the multiple proportions by an example:
Example \(\PageIndex{1}\)
The first compound contains 42.9% by mass carbon and 57.1% by mass oxygen.
The second compound contains 27.3% by mass carbon and 72.7% by mass oxygen.
Show that the data are consistent with the Law of Multiple Proportions!
Solution
In 100 g of the first compound (100 is chosen to make calculations easier) there are 57.1 g O and 42.9 g C.
The mass of O per gram C is:
57.1 g O / 42.9 g C = 1.33 g O per g C
In 100 g of the second compound, there are 72.7 g O and 27.3 g C.
The mass of oxygen per gram of carbon is:
72.7 g O / 27.3 g C = 2.66 g O per g C
Dividing the mass O per g C of the second (larger value) compound by the mass O per g C of the first compound gives:
2.66 : 1.33 = 2 : 1
2 and 1 are both integer numbers.
Dalton's Atom Hypothesis
Dalton argued that atoms could explain the law of the multiple proportions. If one assumed that elements were made of the same type of indivisible particles, that are identical in mass and all properties then, because these particles can only come in integer numbers, different atoms can be combined to form compounds also only in integer numbers. Thus, in a pure compound atoms of unlike elements would be combined in small whole number ratios. Consequently a given compound always has the same relative number and types of atoms. Chemical reactions would involve reorganization of atoms, but the atoms would retain their identity. Atoms could be rearranged in a chemical reaction but not created or destroyed.
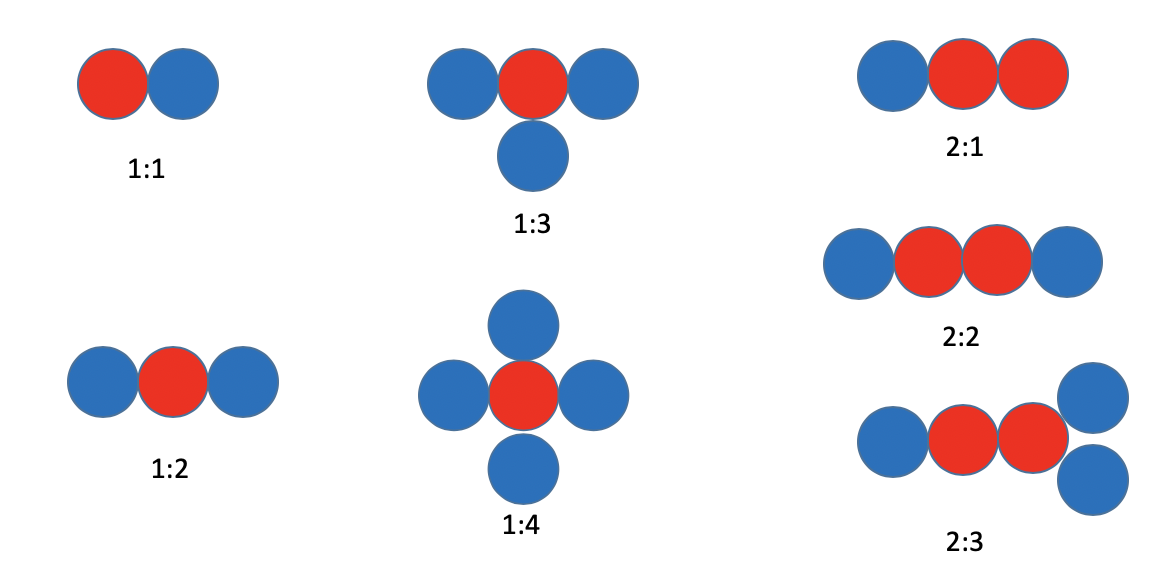
Figure 1.1.7 is a simple illustration how atoms can explain the law of multiple proportions. The blue and red balls symbolize different atoms of different elements. It is possible to combine a red atom with one, two, three, or four blue atoms to make four different compounds. It is for example also possible to combine two red atoms with one, two or three blue atoms. In all of these compounds as well as in all other thinkable ones, the blue and red atoms can only be combined in integer numbers.
Dalton's Atom Symbols
Dalton also thought of symbols for the atoms of the different elements. The symbols are different from the element symbols that are used today, but the concept is the same. You can see some of them in Figure 1.1.8. For example oxygen is represented by a white ball, while carbon is symbolized by a black ball. You can also see that Dalton already combined atom symbols of different elements to illustrate compounds. For example he combined one white ball with one black ball to indicate carbon monoxide, while he combined two white balls with one black ball to indicate carbon dioxide. In this case he correctly identified the ratios of atoms in the two compounds. However, you can see that this is not always the case. For example, he combined one hydrogen atom (white ball with a dot in the middle) with one oxygen atom to indicate the composition of water. However, as we know today, a water molecule has two hydrogen atoms and one oxygen atom. Why has he been right with the carbon-oxygen compounds, but wrong about the water? The answer is that at the time he could determine the atom ratios only from the law of the multiple proportions. At the time there was only one compound known that was made of hydrogen and oxygen, water, so he assumed the simplest atom ratio of 1:1. If he had known hydrogen peroxide, which has the composition H2O2, and thus half as much hydrogen per oxygen, he would have probably correctly assigned the correct hydrogen to oxygen ratio to water. In the case of the carbon oxides, he assigned the compositions correctly because both carbon monoxide and carbon dioxide were known at the time.

https://commons.wikimedia.org/wiki/F...an_symbols.png)
Subatomic Particles
Dalton’s atomic theory stated that different elements were made of different atoms, but did not explain what made the atoms different. The answer is that atoms are composed of subatomic particles, protons, neutron, and electrons, and the number of the protons and electrons in an atom defines the element it represents. So after all, atoms are not so indivisible. However, an atom can still be seen as the smallest particle that represents the full properties of an element. If an atoms gets divided further into subatomic particles then these properties are being lost. To understand atoms further, we must therefore understand the subatomic particles they are made of. The first subatomic particle that was discovered was the electron. It was found through the investigation of so-called cathode rays which were a mysterious phenomenon at the time. Cathode rays occur when a high voltage of about 10-20 kV is applied to an evacuated tube (0.0001 mm Hg). You can see such a tube with a cathode ray going through in Figure 1.1.9. The big question was: What causes these rays?

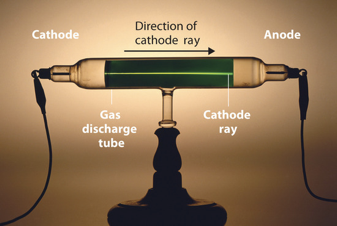
and his experimental apparatus (Attribution: Chemlibetexts https://chem.libretexts.org/@api/dek...338&height=228, creativecommons.org/licenses/by-nc-sa/3.0/us/).
The answer was found by John Joseph Thomson. He applied electric and magnetic fields to these rays and found them deflected. When an electric field was applied the beam was deflected toward the positive pole. When an equally strong electric and magnetic field was applied, and the magnetic field was perpendicular to the electric field then these fields canceled out, and the rays were no longer deflected. Thomson concluded that these rays must consist of negatively charged particles emitted by the negatively charged electrode because they were attracted by the positive pole of the electric field: Electrons. Knowing the forces associated with the electrical and magnetic fields, he was able to calculate a mass to charge ratio of the electrons which is 5.6857 x 10E-9 g/C. After Thomson, Robert Millikan performed another experiment, the so-called oil drop experiment, that allowed to determine the charge and the mass of the electron. The charge of an electron is -1.6 x 10E-19 C, and its mass is 9.1 x 10E-28 g.
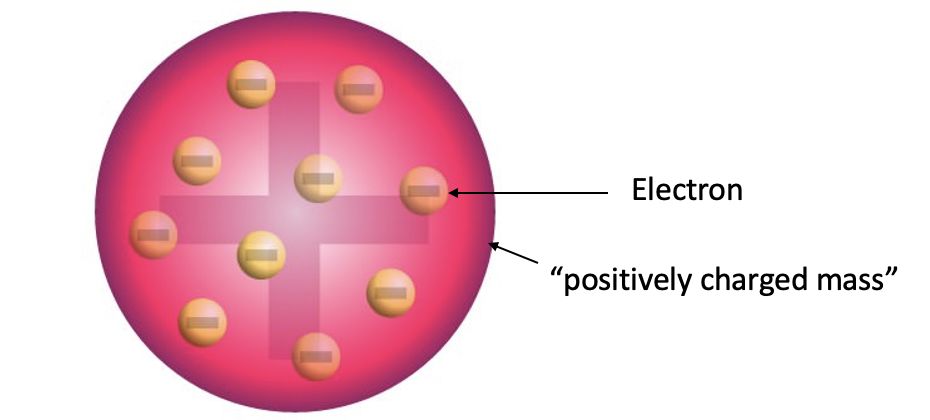
Thomson’s plum pudding atomic model
The discovery of the electron led Thomson to the development of a first atomic model that would include a subatomic particle. It is named plum pudding model (Fig. 1.1.10). In the Thomson atom model electrons are embedded as little particles in a positively charged mass like raisins are embedded in a cake. This atom model is still far from the atom model that we accept today, but it represented an important step forward, because it introduced for the first time the idea that atoms are not indivisible, but contain subatomic particles.
Rutherford's Atom Model
Ernest Rutherford (Fig. 1.1.11) wanted to test Thomson’s plum pudding atom model by experiment. To do so, he placed a photographic film around a gold foil (Figure 1.1.12). In the following he bombarded the gold foil with alpha radiation. Alpha radiation is a form of radioactivity and consists of helium nuclei, also called alpha-particles. It was known at this time the alpha-particles were positively charged and had a large mass compared to an electron. Rutherford’s hypothesis was that if Thomson’s atom model was true, then the alpha particles should all go straight through the gold foil like a bullet going through a plum pudding. Therefore, a blackening of the photographic film, which served as the alpha radiation detector, should only occur directly behind the gold film.

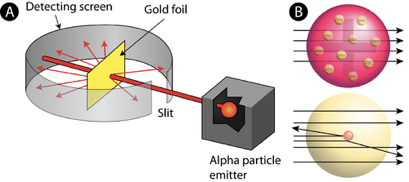
However, what Rutherford observed was that while most of the alpha-particles went straight through the gold foil, some of them were deflected, and a few of them were even reflected. Rutherford concluded that Thomson’s plum pudding model must be wrong. A bullet shot at a plum pudding would just never be reflected by the plum pudding and come back at you.
He suggested that the atom would be made of a positively charged nucleus where almost the entire mass of the atom would be concentrated. In the event of a collision between the alpha particle and that nucleus, the alpha particle would be reflected. In the event of an alpha particle passing by the nucleus close, the alpha particle would be deflected. In the event of an alpha particle passing the nucleus in larger distance, the alpha particle would pass the atom practically non-deflected. The observation that most of the alpha particles were not deflected led Rutherford to the conclusion that the overall atom must be much larger than the nucleus, in fact, the data allowed him to calculate that the radius of the atom would be about 10,000 times larger than the radius of the nucleus. This implies that the atoms would be mostly empty space. To explain the empty space, Rutherford assumed that the electrons would move in orbits around the nucleus like planets around the sun. This would be called the planetary model of the atom (Fig. 1.1.13).
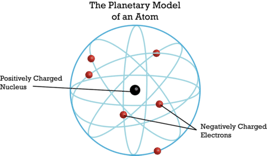
Bohr's Atom Model
Rutherford’s atom model was another big step forward in the development of atomic theory, however there were inherent problems with it as it violated fundamental principles of physics. An electron in an orbit is a self-accelerating electrically charged particle, and according to the laws of physics such particles must emit electromagnetic radiation. However, under normal circumstances atoms do not emit electromagnetic radiation. Secondly, even if the electron emitted electromagnetic radiation, then this would mean that the electron would lose energy because electromagnetic radiation is a form of energy. However, an electron constantly losing energy would make it unstable in its orbit around the nucleus, and it should spiral downward closer to the nucleus until the atom was eventually collapsed. It is however, experimentally not observed that atoms collapse, they are quite stable species. These difficulties of the Rutherford atom model meant that it could not be the final answer to atomic structure. Niels Bohr (Fig. 1.1.14) was aware of the problems of the Rutherford model, and two new developments in physics, namely the concept of the quantization of energy and atomic spectra helped him to develop an improved atom model, known as Bohr model. To understand this model let us look first at the quantization of energy and atomic spectra.

Blackbody Radiation
The quantization of energy was discovered in the context of the physical phenomenon called “blackbody radiation”. Blackbody radiation is the electromagnetic radiation any object sends out due to its temperature (Fig. 1.1.15).

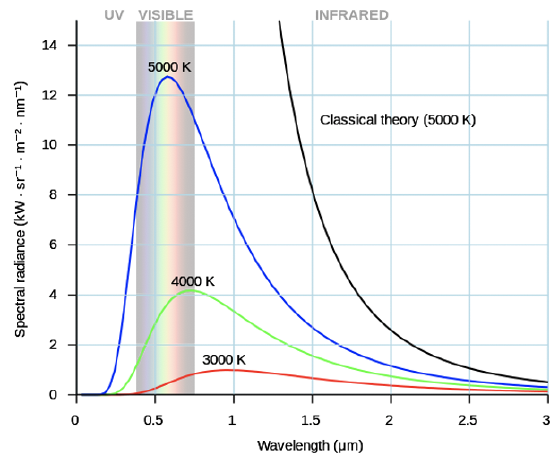
It’s distribution of wavelengths follows curves that depend on the temperature and are shown in Figure 1.1.16. You can see that for each temperature the intensity first increases with increasing wavelength, then goes through a maximum, and finally decreases again. You can also see that the overall intensity of the blackbody radiation increases with temperature and that the maximum of the curve shifts to smaller wavelengths with increasing temperature. Objects at room temperature do not emit much blackbody radiation and the wavelengths are far longer than visible for the human eye. However, when an object is heated high enough, intensity increases and wavelength decreases, and the object starts to glow. For instance, lava (Figure 1.1.15) has a temperature high enough so that its blackbody radiation is visible for the human eye. With increasing temperature objects first glow red, then orange, then yellow, and eventually white. This is because red is the color associated with the largest wavelength, and as temperature increases other colors mix into red, until the object glows white. At extremely high temperatures the blackbody radiation also has a significant intensity in the UV region. Such temperatures occur in welding processes, for example, and for this reason welders need to wear glasses that block the UV radiation. The wavelength and intensity of blackbody radiation can be easily measured, but at the beginning of the 20th century there was no good explanation for its behavior. Classical theory predicted that intensity would continuously increase with decreasing wavelength at any temperature which was not in accordance with experimental observation.
To bring experiment and theory in accordance, Max Planck made the radical assumption that the energy associated with radiation of a given wavelength or a given frequency was quantized. It would be an integer multiple n of that frequency \(\nu\), multiplied with proportionality constant h, know today as the Planck constant.

Equation 1.1.1 The Planck-Einstein equation.
Using this assumption he was able to derive the Planck equation (Equation 1.1.2) which correctly describes the intensity and wavelength distribution of the blackbody radiation for any temperature. The correct description of blackbody radiation strongly supported Planck’s assumption that energy was quantized, but it did not prove it or explain it. The proof and the explanation was found only later. Initially Planck assumed it merely to fit the data.

Equation 1.1.2 Planck's equation
Bohr's Atom Model
The second development that contributed to Bohr’s atom model was the absorption and emission spectra of atoms. It was experimentally observed that under certain circumstances atoms would send out or absorb electromagnetic radiation of discreet wavelengths that were characteristic for an atom. For example, H atoms would absorb or emit at four discreet wavelengths in the visible region of the electromagnetic spectrum (Fig. 1.1.17).

This is known as the Balmer series named after its discoverer Johann Balmer. Friedrich Paschen and Chester Lyman later found that H also absorbs and emits at discreet wavelengths in the IR and UV region respectively. These wavelengths are known as the Paschen and Lyman series, respectively (Fig. 1.1.18).


For the absorption and emission spectra of H a simple mathematical relationship between the energies associated with the wavelengths can be found. The energy is proportional to a constant, today known as the Rydberg constant, times one over an integer number square minus one over another integer number square, whereby the second integer number would be larger than the first one (Eq. 1.1.3). The observation of integer numbers showed that also the energy and the wavelengths of the atomic absorption and emission spectra are quantized. The question was what the quantization of the absorption spectra meant for atomic structure.
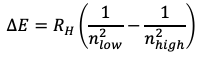
Equation 1.1.3 Rydberg formula for the emission of light with particular energies.
Bohr answered the question the following way. He argued, that like in the Rutherford model the electrons would move in orbits around the nucleus. A balance of opposite centrifugal forces and Coulomb attractions would hold the electron stable in the orbit. However, because energy is quantized, also the angular momentum of the electron would be quantized, and thus, only discreet radii would be allowed. The most inner orbit would have the quantum number n=1, the next higher orbit the quantum number n=2, and so forth (Fig. 1.1.19).
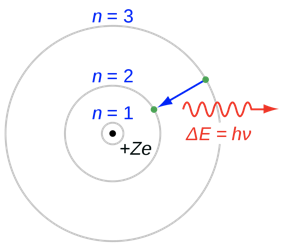
The quantization of the electron energies and the radii would be the explanation why electrons, despite self-accelerating, do not continuously emit electromagnetic radiation. Electromagnetic radiation is only emitted when an electron jumps from an outer orbit of higher energy to an inner orbit of lower energy. This radiation must have a discreet wavelength because the energy difference between two orbits is discreet. Vice versa, an atom can adsorb electromagnetic radiation of specific wavelength and energy that is suitable to make the electron jump from an inner to an outer orbit. In sum, the quantization of the energy and the radii would explain the quantization of the absorption and emission spectra. The question is: Can the radii be calculated, and what are the associated energies of the electrons in the orbits?
Definition: Bohr's Postulates (1913)
1. An electron in an atom moves in a circular orbit about the nucleus under the influence of the Coulomb attraction between the electron and the nucleus, obeying the laws of classical mechanics.
2. Instead of the infinity of orbits which would be possible in classical mechanics, it is only possible for an electron to move in an orbit for which its orbital angular momentum L is an integral multiple of h/2π.
3. Despite the fact that it is constantly accelerating, an electron moving in such an allowed orbit does not radiate electromagnetic energy. Thus, its total energy E remains constant.
4. Electromagnetic radiation is emitted if an electron, initially moving in an orbit of total energy, discontinuously changes its motion so that it moves in an other orbit of total energy. The frequency of the emitted radiation is equal to the quantity divided by h.
To calculate the radii and energies of the electron in the H atom Bohr made two assumptions: Firstly, the centrifugal force associated with the electron moving in the orbit would be assumed equal to the Coulomb force between the electron and the proton so that the electron would be stable in the orbit. Secondly, the angular momentum of the electron would be quantized and an integer multiple of the Planck constant h. The factor 2\(\pi\) is because E = h/2π x angular frequency. The angular frequency (also called angular speed) is the angular displacement (in degree or rad) per time unit. Angular frequency is frequency x 2π. We can rearrange this equation by solving it for v and then insert the equation into equation I giving the result as shown in Fig. 1.1.20.
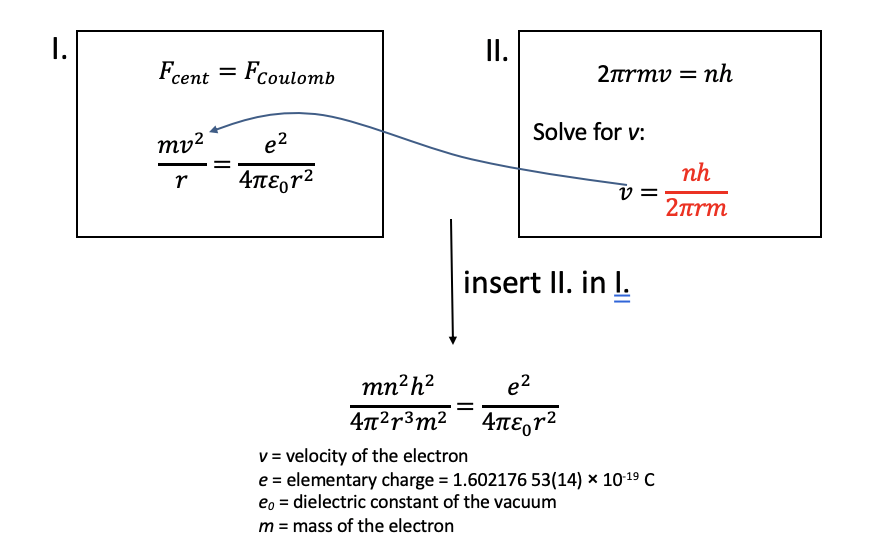
We can then multiply this equation by 4πε0r2, divide by e2, and multiply it by r. This gives us the term r=(n2h2ε0)/(πme2). Analyzing the term shows us that r is only a function of the quantum number n, specifically the radius is proportional to n2 (Fig. 1.1.21). All other terms are constants, namely the Planck constant h, the dielectric constant of the vacuum, π, the mass of the electron, and the elementary charge. By inserting the quantum numbers into the equation we can calculate the actual values for the radii. For example, when we insert 1 for the quantum number n, we get the radius for the most inner orbit of the electron in the H atom. It is 5.29 x 10-11 m. If we inserted 2 for n, we would get the second radius, if we inserted 3, we would get the third radius and so on.
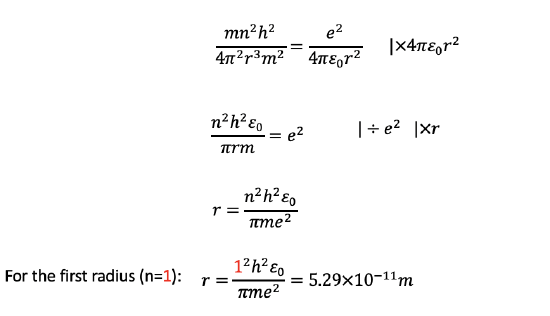
Now let us calculate the energies of the electron on these radii. Generally, the overall energy of the electron is the sum of the kinetic and potential energies. The kinetic energy of a moving object is given by Ekin=1⁄2 mv2. We know that m must be the mass of the electron, but what is the velocity of the electron? We can derive it from equation I we previously used by solving it for v2 (Fig. 1.1.20). We can then insert the term for v2 into the equation Ekin=1⁄2 mv2 , which gives Ekin=e2/(8πε0r), Fig. 1.1.23.
Now let us consider the potential energy. The potential energy is the Coulomb energy between the proton and the electron in the H atom. The formula for the Coulomb energy of two particles having two opposite elementary charges is Epot=-e2/(4πε0r). Note that this energy has a negative algebraic sign because the forces between the proton and the electron are attractive (Fig. 1.1.23).
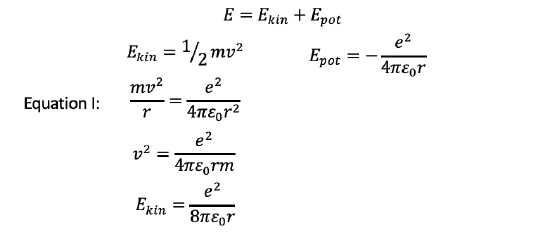
We can now add up the kinetic and the potential energy to give the overall energy which is E = Ekin+Epot= [e2/(8πε0r)] - [e2/(4πε0r)] = e2/(πε0r) (1/8-1/4) = -e2/(8πε0r). We can then use the term we previously calculated for r (Fig. 1.1.21) and insert it into the term for the overall energy. As a result the overall energy becomes E=-(e4m)/(8ε02n2h2), Fig. 1.1.24. As we can see, the energies for the electrons in the different orbits are also only a function of the quantum number n, specifically, they are a function of 1/n2. Note also that the overall energy is negative. This is because the energy is a binding energy. Because of the negative algebraic sign, a higher quantum number n means a higher, because less negative energy. At very high quantum numbers n the value for E would approach zero, meaning that the binding energy for the electron would approach zero. The higher the orbit of the electron the more energy it has and the less strongly it is bound to the atom.
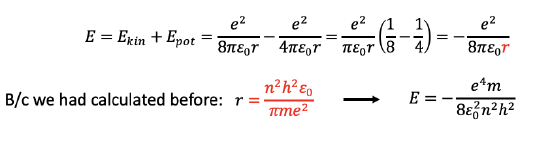
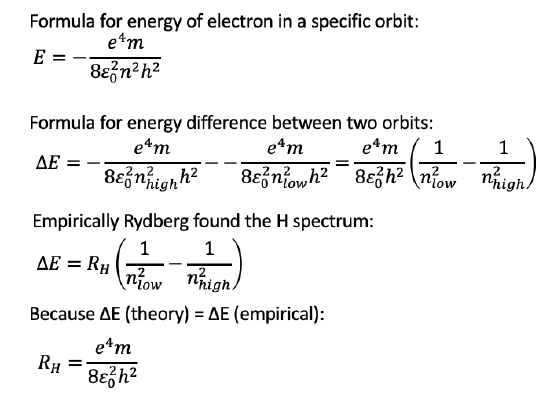
Finally let us calculate energy differences between electrons in different orbits. Subtraction of the terms for the energies of two electrons in two different orbits gives ∆E=(e4m)/(8ε02h2) (1/(nlow2 ) - 1/(nhigh2 )), Fig. 1.1.25. The calculated and empirically found ΔE match excellently, the empirically found Rydberg constant matches the theoretically derived constant (e4m)/(8ε02h2). Thus experiment and theory are in accordance. Bohr’s theory is able to explain the H spectra very well, and can predict both radii of electron orbits and energies. The Bohr model for the first time introduced the quantization of electron states in atoms, and in this regard in was a big step forward. However, there were still problems with Bohr’s theory. It could only explain the H spectra well, but failed to explain the spectra of all other atoms. Secondly, Bohr’s postulates seemed ad hoc and lacked an explanation. There was no good explanation why an electron in a quantized orbit would not emit electromagnetic radiation continuously. Thus, the Bohr model could still not be the final answer to atomic theory. In fact, it lacks to take an important property of the electron into account: The wave-particle dualism of the electron.
Definition: Problems with Bohr's Theory
1. It can explain only the H spectrum and fails to explain all the spectra of all other atoms.
2. Bohr’s postulates are ad hoc. They lack an explanation.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


