15.4.1: Boranes
- Page ID
- 227316
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Boranes and the Bonding in boranes
Boranes were introduced in Chapter 8 (Section 8.6.1). Boranes are compounds consisting of boron and hydrogen.The most basic example is diborane (\(\ce{B2H6}\)), all boranes are electron-deficient compounds. For \(\ce{B2H6}\) usually 14 electrons are needed to form 2c,2e-bonds, but only 12 valence electrons are present. Because of this there are two B-H-B bonds, which have three centers, but only two electrons (3c, 2e bond). This can be interpreted as a molecular orbital that is formed by combining the contributed atomic orbitals of the three atoms. In more complicated boranes not only B-H-B bonds but also B-B-B 3c, 2e-bonds occur. In such a bond the three B-atoms lie at the corners of an equilateral triangle with their sp3 hybrid orbitals overlapping at its center. One of the common properties of boranes is, that they are flammable or react spontaneously with air. They burn with a characteristic green flame. And they are colorless, diamagnetic substances.
Nomenclature
In neutral boranes the number of boron atoms is given by a prefix and the number of Hydrogen-atoms is given in parentheses behind the name. example: \(\ce{B5H11}\) -> pentaborane(11), \(\ce{B4H10}\) -> tetraborane(10) For ions primarily the number of hydrogen-atoms and than the number of boron-atoms is given, behind the name the charge is given in parentheses. example: \(\ce{[B6H6]^{2-}}\) -> hexahydrohexaborat(2-)
Wades rule, Structures of boranes
Wades rule helps to predict the general shape of a borane from its formula. Ken Wade developed a method for the prediction of shapes of borane clusters; however, it may be used for a wide range of substituted boranes (such as carboranes) as well as other classes of cluster compounds. Wade’s rules are used to rationalize the shape of borane clusters by calculating the total number of skeletal electron pairs (SEP) available for cluster bonding. In using Wade’s rules it is key to understand structural relationship of various boranes.
The general methodology to be followed when applying Wade’s rules is as follows:
- Determine the total number of valence electrons from the chemical formula, i.e., 3 electrons per B, and 1 electron per H.
- Subtract 2 electrons for each B-H unit (or C-H in a carborane).
- Divide the number of remaining electrons by 2 to get the number of skeletal electron pairs (SEP).
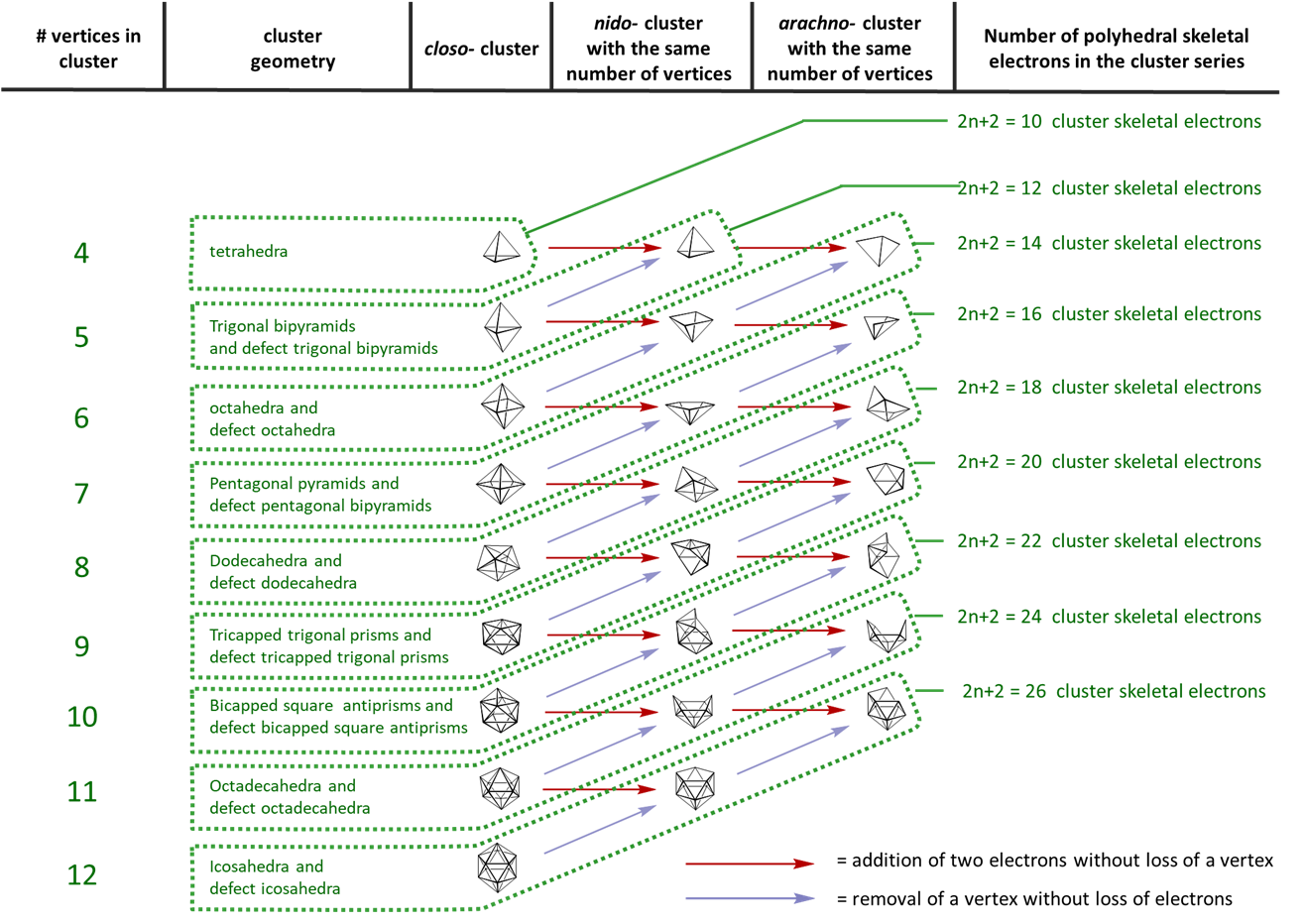
- A cluster with n vertices (i.e., n boron atoms) and n+1 SEP for bonding has a closo structure.
- A cluster with n-1 vertices (i.e., n-1 boron atoms) and n+1 SEP for bonding has a nido structure.
- A cluster with n-2 vertices (i.e., n-2 boron atoms) and n+1 SEP for bonding has an arachno structure.
- A cluster with n-3 vertices (i.e., n-3 boron atoms) and n+1 SEP for bonding has an hypho structure.
- If the number of boron atoms (i.e., n) is larger than n+1 SEP then the extra boron occupies a capping position on a triangular phase.
| Formula Skeletal | Skeletal electron pairs | type |
|---|---|---|
| \(\ce{[B_{n} H_{n}]^{2-}}\) | n+1 | closo |
| \(\ce{B_{n} H_{n + 4}}\) | n+2 | nido |
| \(\ce{B_{n} H_{n + 6}}\) | n+3 | arachno |
| \(\ce{B_{n} H_{n + 8}}\) | n+4 | hype |
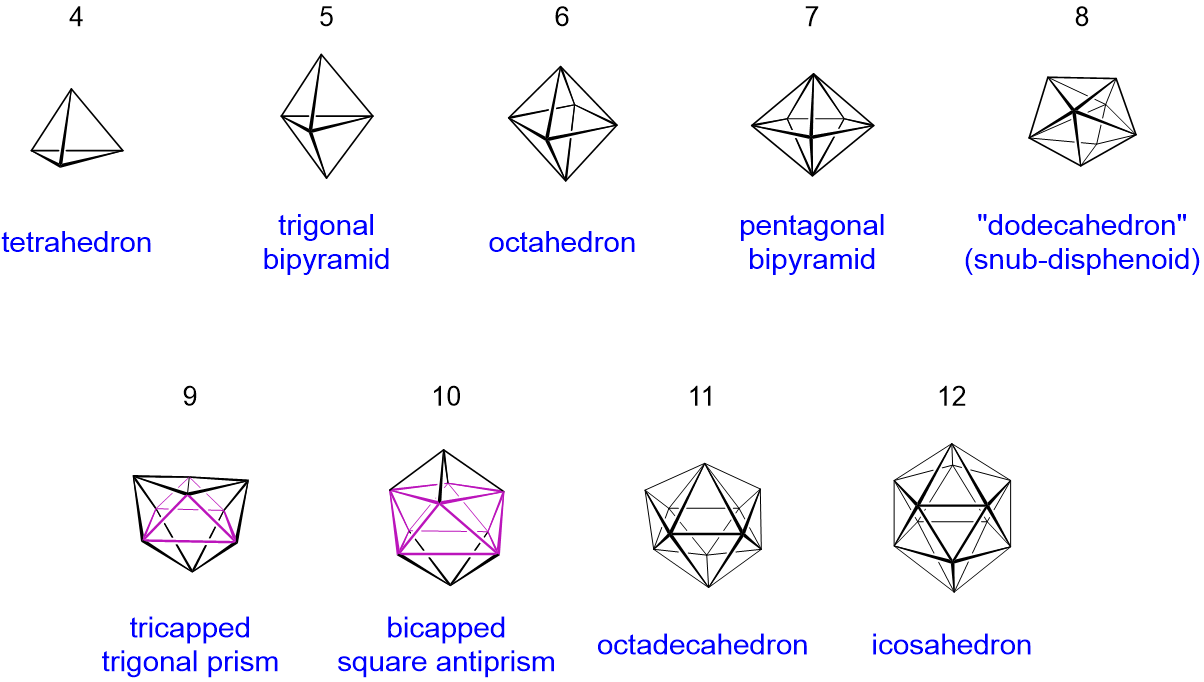
The polyhedra are always made up of triangular faces, so they are called deltahedra. Usually there are three possible structure types:
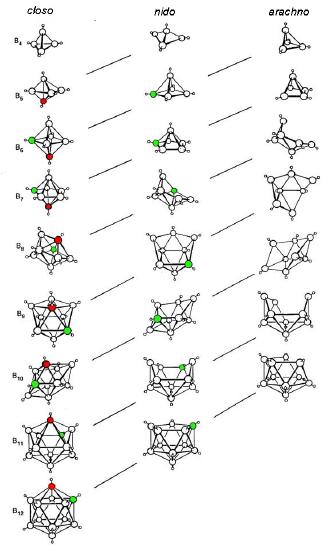
Structural relationship between closo, nido, and arachno boranes (and hetero-substituted boranes). The diagonal lines connect species that have the same number of skeletal electron pairs (SEP). Hydrogen atoms except those of the B-H framework are omitted. The red atom is omitted first, the green atom removed second. Adapted from R. W. Rudolph, Acc. Chem. Res., 1976, 9, 446.
Closo-boranes
- closed deltahedra without B-H-B 3c,2e-bonds
- thermally stable and moderately reactive.
- example: \(\ce{[B5H5]^{2-}}\): the ion builds up a trigonal, bipyramidal polyhedron
Nido-boranes
- closo borane with one corner less and addition of two hydrogen-atoms instead
- B-H-B-bonds and B-B-bonds are possible.
- thermally stability lies between closo- and arachno-boranes.
- example: \(\ce{B5H9}\) its structure can be assumed as the octahedral deltahedron of \(\ce{[B6H6]^{2-}}\) without one corner tetragonal pyramid
Arachno-boranes
- closo borane deltahedron but with two BH-units removed and two H-atoms added.
- it has to have B-H-B 3c, 2e-bonds.
- thermally unstable at room temperature and highly reactive.
- example: \{\ce{B4H10}\) the structure can be derived from \(\ce{[B6H6]^{2-}}\) -> deltahedron with two corners less.
There exist also other structures like the hypho-boranes, but they are less important.
Wade's Rules
What is the structure of B5H11?
Solution
- Total number of valence electrons = (5 x B) + (11 x H) = (5 x 3) + (11 x 1) = 26
- Number of electrons for each B-H unit = (5 x 2) = 10
- Number of skeletal electrons = 26 – 10 = 16
- Number SEP = 16/2 = 8
- If n+1 = 8 and n-2 = 5 boron atoms, then n = 7
- Structure of n = 7 is pentagonal bipyramid, therefore B5H11 is an arachno based upon a pentagonal bipyramid with two apexes missing.
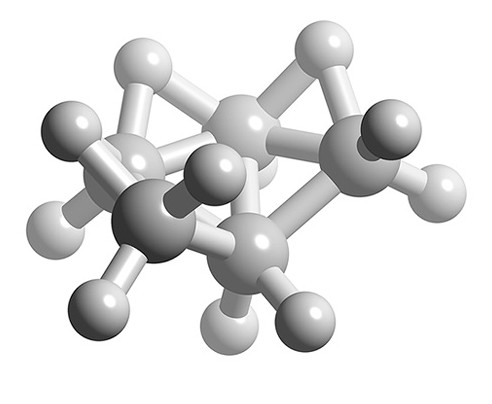
Ball and stick representation of the structure of B5H11.
What is the structure of B5H9?
Solution
- Total number of valence electrons = (5 x B) + (9 x H) = (5 x 3) + (9 x 1) = 24
- Number of electrons for each B-H unit = (5 x 2) = 10
- Number of skeletal electrons = 24 – 10 = 14
- Number SEP = 14/2 = 7
- If n+1 = 7 and n-1 = 5 boron atoms, then n = 6
- Structure of n = 6 is octahedral, therefore B5H9 is a nido structure based upon an octahedral structure with one apex missing.
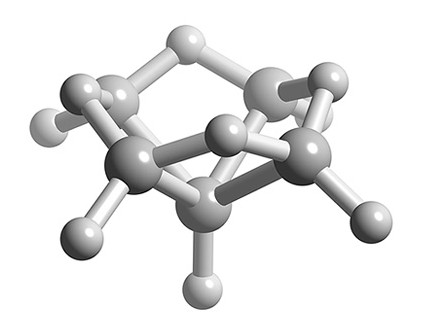
Ball and stick representation of the structure of B5H9.
What is the structure of B6H62-?
- Total number of valence electrons = (6 x B) + (3 x H) = (6 x 3) + (6 x 1) + 2 = 26
- Number of electrons for each B-H unit = (6 x 2) = 12
- Number of skeletal electrons = 26 – 12 = 14
- Number SEP = 14/2 = 7
- If n+1 = 7 and n boron atoms, then n = 6
- Structure of n = 6 is octahedral, therefore B6H62- is a closo structure based upon an octahedral structure.
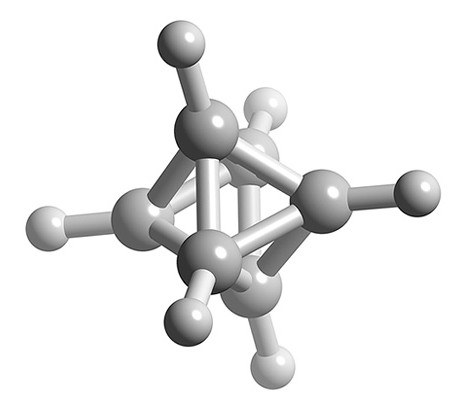
Ball and stick representation of the structure of B6H62-.
Table \(\PageIndex{1}\) provides a summary of borane cluster with the general formula BnHnx- and their structures as defined by Wade’s rules.
| Type | Basic formula | Example | # of verticies | # of vacancies | # of e- in B + charge | # of bonding MOs |
|---|---|---|---|---|---|---|
| Closo | BnHn2- | B6H62- | n | 0 | 3n + 2 | n + 1 |
| Nido | BnHn4- | B5H9 | n + 1 | 1 | 3n + 4 | n + 2 |
| Arachno | BnHn6- | B4H10 | n + 2 | 2 | 3n + 6 | n + 3 |
| Hypho | BnHn8- | B5H112- | n + 3 | 3 | 3n + 8 | n + 4 |

Notes and References
R. W. Rudolph, Acc. Chem. Res., 1976, 9, 446.
K. Wade, Adv. Inorg. Chem. Radiochem., 1976, 18, 1.
D. F. Shriver, P. W. Atkins, Inorganic Chemistry Third edition, Oxford University Press, 2001
Patrick O‘ Malley from the University of Manchester via Wolearn.org (https://www.wolearn.org/pluginfile.php/1492/mod_resource/content/1/Wades_Rules.pdf)
Template:ContribConnectionshttps://archive.cnx.org/contents/ffb...2/wade-s-rules
Contributors and Attributions
Stephen Contakes, Westmont College

