13.3.1: The 18 Electron Rule
- Page ID
- 385575
Method A for counting electrons: The Donor Pair Method
The donor pair method consider ligands to donate pairs of electrons to the metal. Each ligand-metal bond is considered a pair of electrons donated to the metal by the ligand. The method consists of the steps described in the box below.
- Determine the oxidation state of the metal center. This step can be done by first deconstructing the complex so that each ligand "keeps" its bonded electrons (See Figure \(\PageIndex{2}\)). by considering the overall charge of the complex and the charge of each ligand, the oxidation state of the metal center can be determined. An alternative to deconstruction is to consider each ligand's class according to the Covalent Bond Classification (CBC) method discussed earlier.
- Determine the number of metal ion valence electrons. The number of valence electrons can be determined from the metal's group on the periodic table and its oxidation state. If the oxidation state is positive we subtract electrons from the group number, if it is negative, which is rare, then we add electrons.
- Determine the number of bonded electrons derived from ligands. Each ligand single bond provides two electrons, double bonds provide four electrons, etc.
- Add the number of electrons from the metal ion valence (step 2) to the number of bonded electrons from the ligands to get the total valence electron count for the complex.
Below is an example of using the donor pair method to count electrons in the chemotherapy drug \(\ce{cis-[PtCl2(NH3)2]}\), also called cis-platinum (Figure \(\PageIndex{1}\)). This compound is neutral in charge.
Step 1: Deconstruction of the complex using the donor pair method would convert each metal-ligand bond to a pair of electrons on the ligand. Without consulting the Covalent Bond Classification (CBC) method, we can determine the charge on each ligand using the simple Lewis dot diagrams that result. The ligands consist of two neutral ammines and two negatively charged chlorides. The ligands account for a total negative charge of -2. Since the metal complex is neutral, there must be a +2 change on the metal. Thus, the metal oxidation state is +2.
Step 2: With the knowledge that the Pt has an oxidation state of +2, and is in group 10 of the periodic table, we can determine the number of valence electrons on Pt(II). Subtract the oxidation state from the group number to get 8 valence electrons on the Pt(II) ion.
Step 3: Each of the ligands had one bond to Pt, thus each is a 2-electron donor. The ligands combined contribute a total of 8 electrons.
Step 4: Adding the 8 electrons from Pt(II) and the 8 electrons from the ligands gives a total electron count of 16.

Method B for counting electrons: The Neutral Atom Method (aka Neutral Ligand Method)
The “neutral atom method”, is sometimes called "the neutral ligand method". In this method, each ligand is considered to donate the number of electrons that it would if the ligand were neutral. The neutral atom method is carried out according to the steps described below.
- Determine the number of valence electrons on the metal center, as if it were a neutral atom. Add those electrons to the total count.
Hint: The number valence electrons is the same as the group number of the transition metal in the periodic table (groups 3-12 for the transition metals). - Account for the ionic charge on the entire coordination complex. If the charge is neutral, you can ignore this step. If the complex has a positive charge, you subtract that many electrons from the total count. If the complex is an anion, you add the anionic charge to the total electron count.
- Determine how many electrons are contributed by each ligand. (This is the most complicated step)
- Deconstruct the metal ion (break its M-L bonds) so that each resulting ligand fragment and the central metal are neutral.
- Then count the number of electrons from each ligand that contributed to the bond. Add the sum of those electrons from all the ligands to the total count.
(Remeber you've already accounted for the electrons from the neutral atom in step #1)
- Add the metal ion valence electrons (step 1), the total ligand electrons (step 3), and accounting for the charge of the complex (step 2). The total sum is the total valence electron count for the metal complex.
Below is an example of applying the neutral atom method to count electrons in the cis-platinum complex (\(\ce{[Pt(Cl)_2(NH_3)_2]}\) (Figure \(\PageIndex{2}\))).
Step 1: The metal is platinum which is located in group 10 of the periodic table. Therefore, a neutral platinum atom has ten valence electrons.
Step 2: The complex is neutral, this we can ignore this step.
Step 3: Each Cl is considered to donate 1 electron and each ammine ligand is considered to donate two electrons. The Cl's donate a total of two electrons, and the ammines donate a total of four electrons to give a total of 6 from all ligands.
Step 4: Ten electrons from Pt and six electrons from the ligands combine to give a total electron count of 16.

There are pros and cons to each of the methods presented above. The neutral atom method has the advantage that we do not have to calculate charges of ligands or the metal oxidation states to reach the final answer. However, the disadvantage is that we must think about how to cleave bonds to create neutral fragments. We may need to cleave bonds in an way that is contrary to the real donor-acceptor nature of a coordination compound. The donor-pair method does account for the donor-acceptor nature of a coordination compound because the bonds are considered dative bonds, and the electrons are assigned to the ligands and metals accordingly. And advantage to the donor-pari method is that we do not need to think how to cleave bonds in artificial ways because we cleave the bonds always heteroleptically. However, the disadvantage is that it requires us to calcuate charges at the ligands to determine metal oxidation states, which is an additional, non-trivial step.
The 18 Electron Rule
Electron counting is a critical step in the context of an important rule in coordination chemistry: The 18 electron rule. The 18 electron rule states that transition metal complexes are normally most stable when they have a total count of 18 electrons in the valence shell. In other words, for \(d\)-block metal complexes, a valence configuration that fills all valence orbitals (\(ns^2 \; (n-1)d^{10} \; np^6\)) is most stable; it is equivalent to a nobel-gas configuration for the metal atom, and is analogous to the "octet rule" for the main-group elements. Complexes that have 18 electrons in their count are considered to be coordinatively saturated. In general, coordinatively saturated compounds are considered to be relatively stable, and when they react they usually undergo dissociation or oxidation reactions that decrease the electron count. If the there are less than 18 electrons, the species is coordinatively unsaturated, and considered less stable than a species with 18 electrons. In general, coordinatively unsaturated complexes tend to react in ways that can increase the electron count. They tend to undergo reactions involving associations to add more electrons to the system and/or tend to gain electrons through redox reactions (the metal becomes reduced). If a species has more than 18 electrons it is coordinatively oversaturated and tends to lose ligands. It is usually easily oxidized. Both loss of ligands and oxidation reduces to the number of electrons to or at least closer to 18.
Coordinatively saturated: when the complex has an electron count =18 electrons. These complexes are considered most stable.
Coordinatively unsaturated: when the complex has an electron count <18 electrons. These complexes tend to add more ligands, and to become reduced.
Coordinatively oversaturated: when the complex has an electron count >18 electrons. These complexes tend to lose ligands and become oxidized.
Exceptions to the 18-electron rule:
The 18 electron rule has many exceptions, and therefore needs to be applied with caution. In particular, group 3, 4, and 10 complexes deviate often from the 18 electron rule.
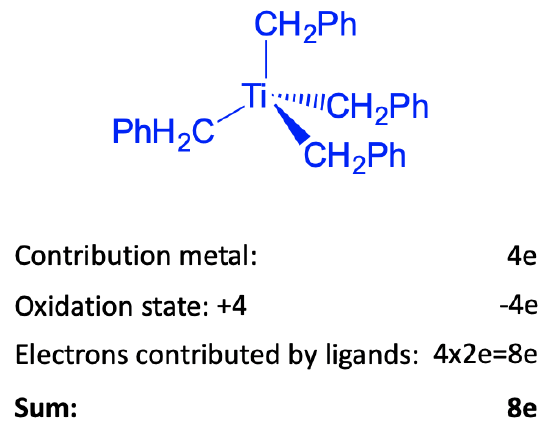
For illustration purposes, let us count the number of electrons of the tetrahedral tetrabenzyltitanium(0) complex by the oxidation state method. We could also use the neutral atom method, which would give the same results. This complex is a group 4 complex because titanium is in group 4. How many electrons will the titanium contribute? Because the number of electrons is always the same as the group number, it will contribute four electrons. Next, what is oxidation state of Ti? To determine it we must determine the charge at the ligands. To do that we cleave the bonds heteroleptically. This will give benzylate anions with -1 charge. There are four of these ions, and therefore there will be four negative charges overall. The complex is charge-neutral, and thus the oxidation state is +4 because -4+4=0. Therefore, we need to subtract four electrons. Because we cleaved the bond heteroleptically, each ligand contributes two electrons, giving overall eight electrons coming from the four ligands. This means that we have overall eight electrons, or an 8-electron complex. This is far, far away from 18 electrons. Nonetheless, the complex is stable. How can we explain this? The answer is that in order to achieve 18 electrons it would need to add five additional ligands if each ligand is considered a 2-electron donor. This would increase the coordination number to 9 which is too high to produce a stable complex. In order to reduce the complex to an 18 electron complex, 10 electrons would need to be added. This would produce a complex with a -10 charge which is way to high to be stable. The arguments are generalizable for group 3 and group 4 complexes. Because these elements only have a few d electrons, the ligands would need to contribute a lot of electrons to produce an 18 electron complex. This would require just too many ligands to add. The coordination numbers would get too high. If electrons are added instead of ligands, the negative charge at the complex would be to high to be stable based on electron-electron repulsion arguments.
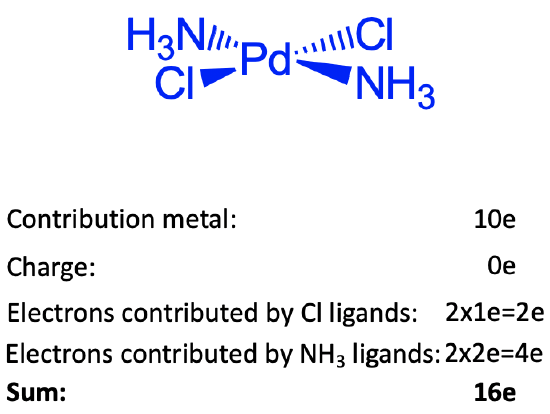
These arguments cannot be applied for group 10 elements, because these elements have many d electrons. The explanation in this case is that these elements like to make square planar complexes when in the oxidation number is +2. Square planar complexes prefer 16 instead of 18 electrons. We will learn later, when we discuss bonding in coordination compounds, why this is. You can see that the square planar diamminedichloro palladium complex shown is square planar and has sixteen electrons. There are 10 electrons coming from Pd. If we use the neutral atom method, no electrons need to be added or subtracted due to the charge at the complex. The complex is charge-neutral. To assess how many electrons come from the ligands we need to cleave the bonds so that neutral ligands are produced. The Pd-Cl bonds need to be cleave homoleptically, the Pd-N bonds need to be cleave heteroleptically. Therefore, the two chloro ligands are 1e donors, and the two ammine ligands are 2e donors. This gives 10+4+2=16 electrons.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.


