12.5.3: Isomerization of Chelate Rings

Last updated
Save as PDF

Page ID: 390573

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Recall that the stereoisomers of octahedral complexes with two and three bidentate ligands were discussed previously (Section 9.3). This page will discuss the interconversion of stereoisomers, which can occur through two primary mechanisms involving either (1) bond breaking and bond making steps, and (2) twisting.

Isomerization through dissociative substitution

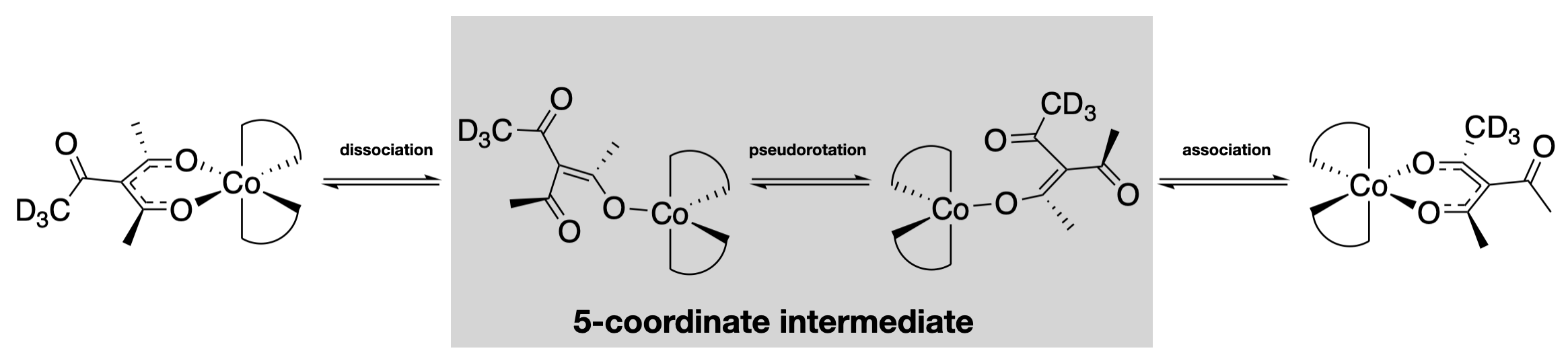
One way to convert one steroisomer to another is through bond breaking and bond re-making steps. This type of structural rearrangement is essentially a substitution reaction, as described previously in this chapter, except that the leaving group and entering group are the same ligand. Evidence for this type of mechanism comes from the study of isotopically labeled amibidentate ligands (those that have different modes of coordination). For example, an acetyl group with a labeled \(\ce{CD3}\) can be added as an "outside" group (adjacent to the coordinating groups) in a tris(acac)cobalt(III) complex. The labeled group moves to the "inside" (directly coordinated to the metal ion) during isomerization from an optically pure solution to a racemic mixture. This change can only occur through bond breaking and re-forming steps.

Figure \(\PageIndex{1}\): The rearangement of a \(\ce{CD3}\) group from an "outer acetyl" to one directly coordinating to the metal complex of an \(\ce{CD3}\)-labeled acetyl group on acetylacetone (acac) provides evidence of isomerization through a mechanism related to dissociative substitution. (CC-BY-SA; Kathryn Haas)

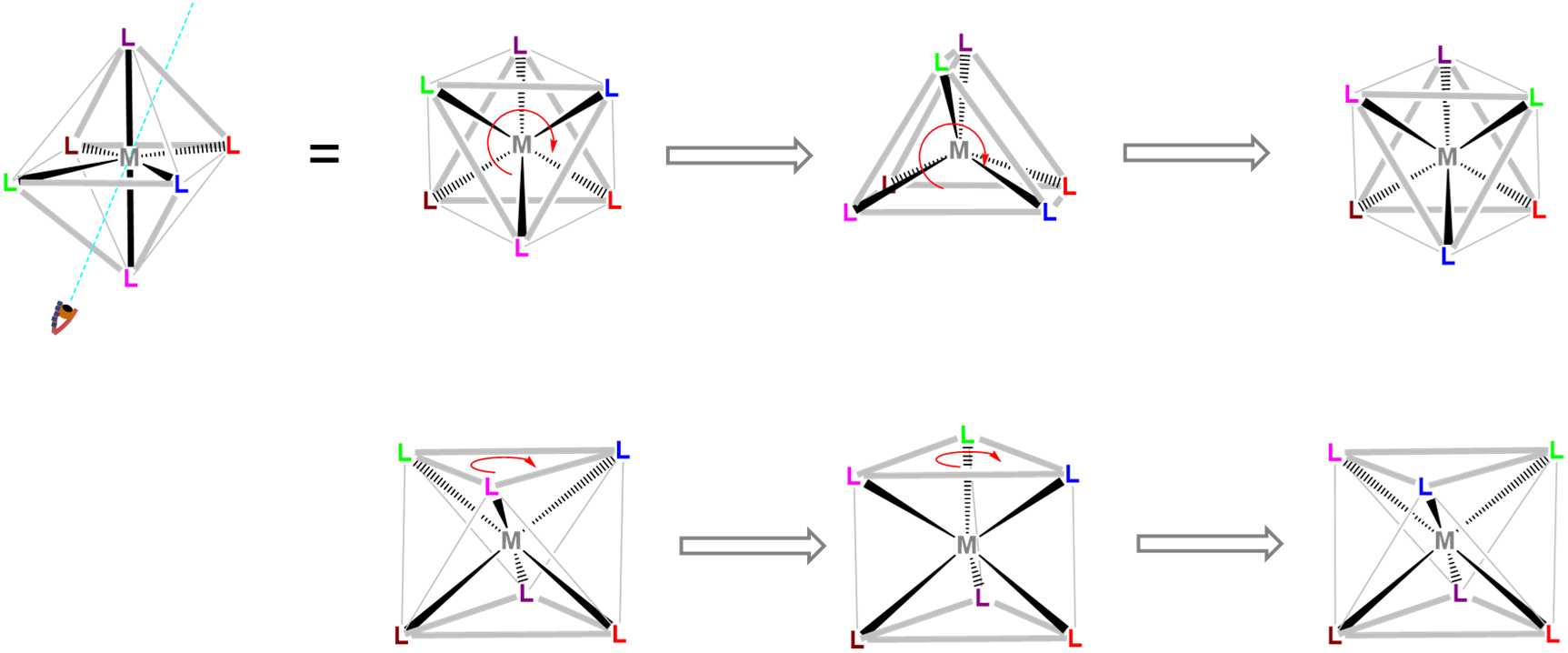
Isomerism through twisting

The second pathway of isomerism is through twisting; it does not involve bond breaking or bond forming. Twisting that causes interconversion of octahedral isomers was also discussed in Chapter 9. A figure from that chapter is re-posted here for convenience.

An octahedroal coordination sphere is just a trigonal antiprism in which all edge lengths are identical. Rotation of one triangular face relative to its opposite until the two are eclipsed gives a triganal prismatic geometry. In fact, since continuation of this rotation gives another octahedral complex the trigonal prismatic geometry is an intermediate in isomerization reactions involving octahedral complexes. In tris- and bis-chelates such isomerizations are said to occur by a Bailar twist or a Ray-Dutt twist, which differ only in the relationship between the chelate rings and the faces twisted.

Figure \(\sf{\PageIndex{2}}\). Since an octahedron is a trigonal antiprism a trigonal prism may be produced by rotating or "twisting" one face of the octahedron relative to its opposite. Since continuation of the rotation gives an isomer of the original octahedron, when the energy landscape for twists like these is thermally or photochemically accessible twists like these provide one pathway for isomerisation reactions involving octahedral complexes. In tris- and bis-chelates such isomerizations are said to occur by Bailar and Ray-Dutt twists, which differ only in the relationship between the chelate rings and the faces twisted. Top: View down looking down an axis bisecting a pair of opposing faces. Bottom: View perpendicular to that shown at top. This work by Stephen Contakes is licensed under a Creative Commons Attribution 4.0 International License.