12.4.2: Linear Free Energy Relationships

Last updated
Save as PDF

Page ID: 385542

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Linear Free Energy Relation (LFER) is a tool that can indicate the importance of bond breakage or bond formation in the rate-determining step. In the case of a dissociative mechanism, for example, bond breaking is critical for reaction progress. Therefore, the strength of the M-X bond influences not only the extent to which the reaction will happen, but also the rate. Although thermodynamic stability of a complex does not necessarily indicate the kinetic rate at which it will react, there is a relationship between bond stability and the rate of reaction if the breaking or formation of that bond is involved in the rate-determining step. The relationship can be stated as follows:

\[ln \; k = ln \; K +c \nonumber \]

And this relationship can be justified using the Arrhenius equation and equation for the temperature-dependence of the equilibrium constant.

\[\ln k=\ln A-\frac{E_{A}}{R T} \quad \text { and } \quad \ln K=\frac{-\Delta H^{\circ}}{R T}+\frac{\Delta S^{\circ}}{R} \nonumber \]

In an experiment designed to test the Linear Free Energy Relationship, several reactions would be conducted under nearly identical conditions, where only the identity of the leaving group, X, is varied. In these experiment, the temperature would be constant and the same in each case. If we assume that the pre-exponential factor, \(A\) is the same for each reaction condition (and it should be at identical temperatures for analogous reactions), then the \(\ln K\) term of the Arrhenius equation becomes proportional to the activation energy, \(E_a\) (and proportional to Gibb's energy of activation, \(\Delta G^{\ddagger} \), and Gibb's energy \(\Delta G\)). And since the Gibb's energy is related to the equilibrium constant, K, by \(\Delta G = RT \ln K\), the value of \(K\) and \(k\) should be correlated. Likewise, if \(T\) is constant over the reaction conditions and \(\Delta S^{\circ}\) is similar across the analogous reactions (which it should be), then \(\ln K\) becomes proportional to enthalpy, \(\Delta H^{\circ}\), which is proportional to Gibb's free energy of reaction \(\Delta G^{\circ}\).

If a Linear Free Energy Relation plot of \(\ln K\) vs \(\ln k\) is linear, but with a slope less than one, it indicates a dissociative mechanism with some degree of associative character (for example, an \(I_d\) mechanism or a mechanism involving the formation of preassociation complex). If the plot of \(\log K\) vs \(\log k\) for the reactions is linear, this is evidence that the reaction is dissociative. An example for a linear free energy plot is shown in Figure \(\PageIndex{1}\) for the hydrolysis of \(\ce{[Co(NH3)5X]^+2}\) (this is the substitution of \(\ce{X^-}\) with \(\ce{H2O}\)).

Figure \(\PageIndex{1}\): Linear Free Energy relationship lot for \(\ce{[Co(NH3)5X]^+2}\) where \(\ce{X^- = F^-, H2PO4^-, Cl^-, Br^-, I^-, NO3^-}\). This is summarized in Cooper H. Langford, Inorganic Chemistry **1965** 4 (2), 265-266, DOI: 10.1021/ic50024a041. (CC-BY-SA; Kathryn Haas)

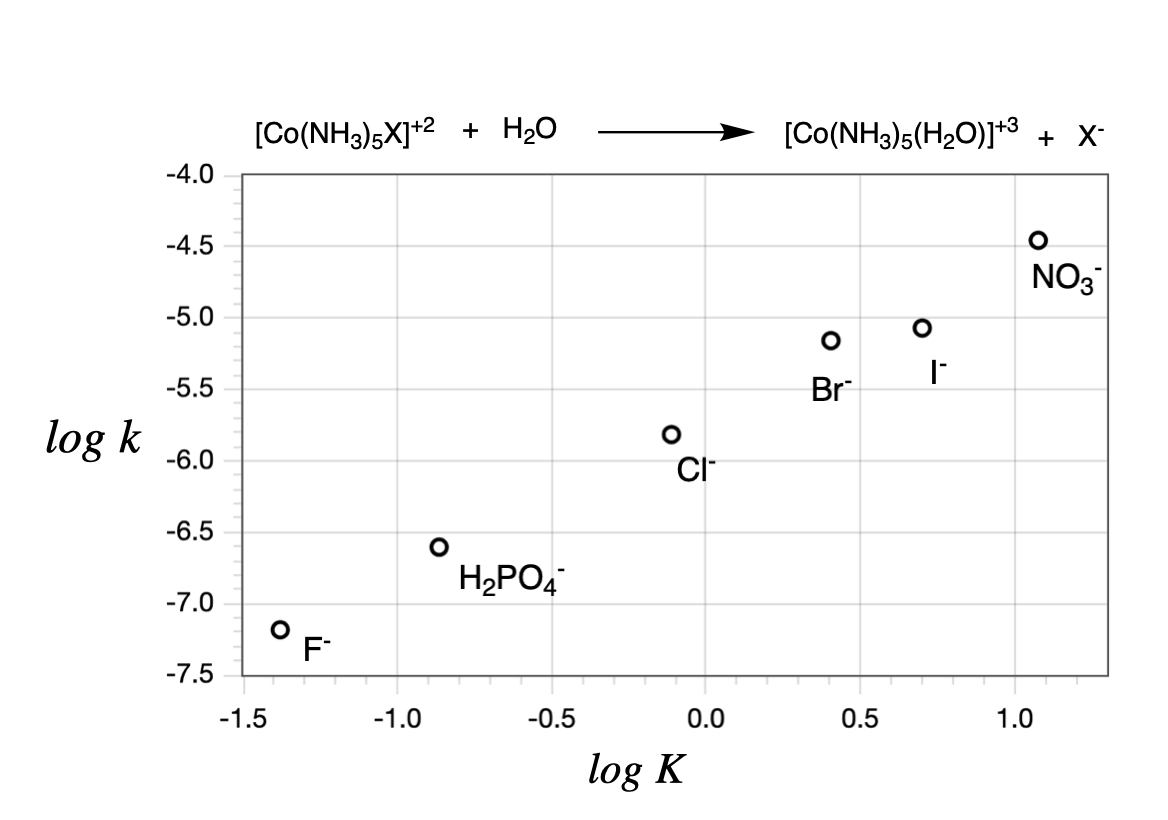
When the slope is approximately 1, as it is in the case of \(\ce{[Co(NH3)5X]^+2}\) in Figure \(\PageIndex{1}\), it indicates that the variation of the \(\ce{X^-}\) leaving group has a similar effect on the magnitude of both \(\Delta G\) (thermodynamic, related to \(K\)) and \(\Delta G^{\ddagger}\) (kintetic, related to \(k\)). In other words, a slope close to 1 indicates a purely dissociative pathway (D). This data shown in Figure \(\PageIndex{1}\), for example, is evidence of a dissociative mechanism for \(\ce{[Co(NH3)5X]^+2}\).

The argument that a reaction is dissociative can also be supported by evidence showing little effect of the incoming ligand on reaction rate. For example, data supporting the argument that \(\ce{[Co(NH3)5H2O]^+3}\) reacts by a dissociative pathway is shown below. The data show that variation of the identity of the incoming ligand, \(\ce{Y^-}\), has little effect on the rate constant (they are approximately within one order of magnitude).

\[ \text{For the reaction: }\ce{[Co(NH3)5H2O]^3+ + Y^{m-} <=> [Co(NH3)5Y]^{(3-m)+} + H2O} \nonumber \]

Table \(\PageIndex{1}\): Rate Constants for Exchange of Aquo Ligand of pentaammineaquo cobalt(III) ion by incoming ligand, Y (chemical equation shown above). There is little effect of the identity of the incoming ligand on the rate constant. This data was sourced from Miessler, Fischer and Tarr's *Inorganic Chemistry,* *5th edition*, pg 448.
Entering Ligand, \(\ce{Y^-}\)	Rate Constant, \(k_1 \; (10^{-6}s^{-1})\) (pseudo-first order with excess \(\ce{[Y^{-}]}\))
\(\ce{H2O}\)	100
\(\ce{N3^-}\)	100
\(\ce{SO4^2-}\)	24
\(\ce{Cl^-}\)	21
\(\ce{NCS^-}\)	16