12.4.1: Dissociation

Consider what must happen for the simplest case of a purely dissociative (D) reaction mechanism for an octahedral metal complex. The first step, and the rate-limiting step must be dissociation of one ligand to form an intermediate with a lower coordination number. Such a situation, where an octahedral complex looses a ligand, X, to become a square pyramidal intermediate is shown below in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Dissociation of a ligand to form a square pyramidal intermediate. This would be the first step of a dissociative (D) reaction mechanism. The Ligand Field Activation Energy (LFAE) can be calculated from the splitting energies of the octahedron compared to the square planar intermediate. (CC-BY-SA; Kathryn Haas)

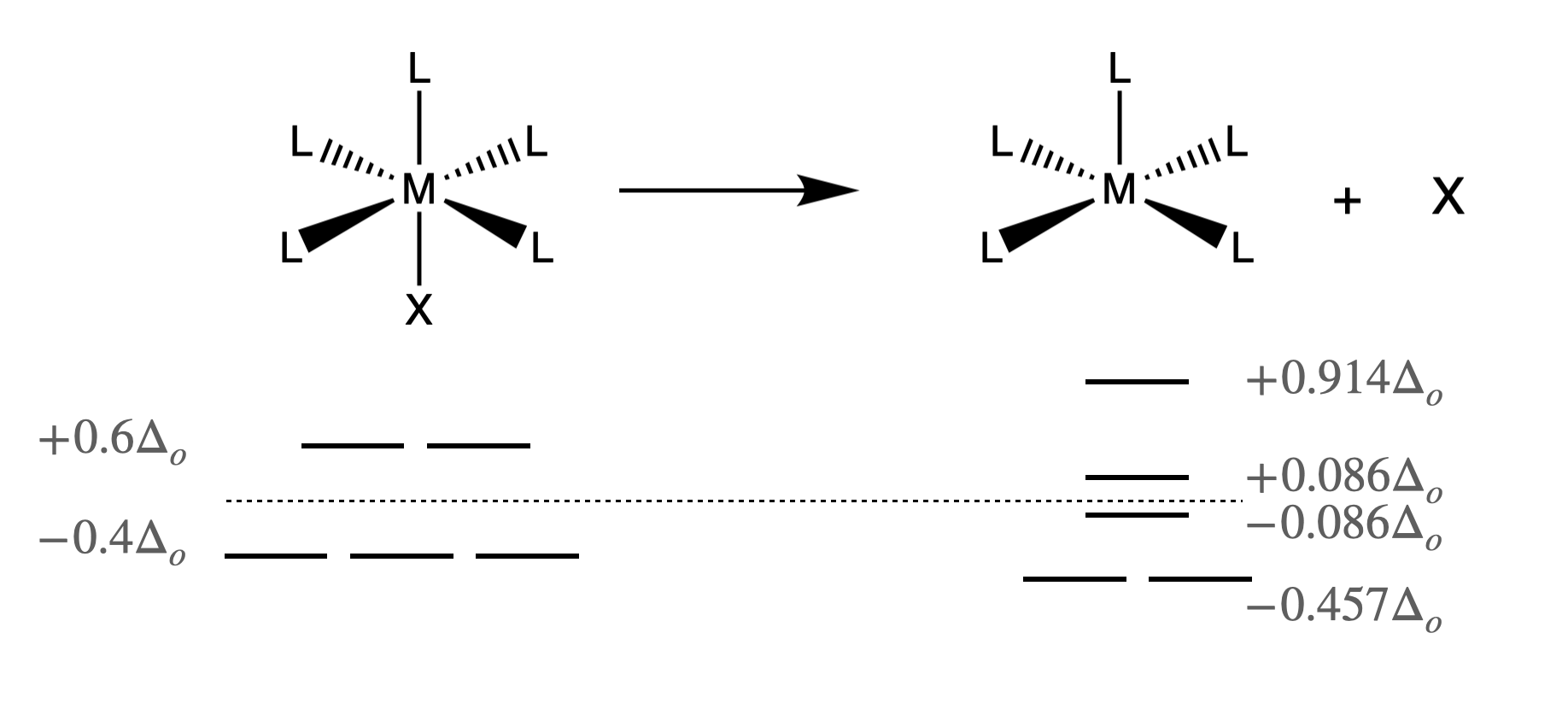
If the dissociation of a ligand is rate-determining, factors that lower the energy of the transition state or intermediate structures will speed the reaction rate. Here we could consider the differences in ligand-field stabilization energy (LFSE). The difference between the LFSE of the octahedral reactant and that of the intermediate is defined as the ligand field activation energy (LFAE). The LFAE can be calculated for a given \(d\)-electron count for an octahedral reactant and a square pyramidal intermediate using the information provided in Figure \(\PageIndex{1}\). Metal ions with particularly low (more negative) LFAE values tend to be more labile, while those with particularly high (less negative) values tend to be more inert. However, most octahedral complexes are expected to react through dissociative mechanisms due to the unfavorable steric crowding that must occur during an associative pathway.

The ease by which the M-X bond is broken will also influence rate of a dissociative reaction, and this can be probed experimentally. The following experiments can give evidence that support the argument that a reaction occurs by a dissociative pathway, or that it is dissociatively activated.

Experimental evidence that supports dissociative mechanism

1. Identity of the entering ligand has little effect on reaction rate.

If dissociation is the rate-determining step, the identity of the entering ligand, Y, should have little effect on the reaction rate. Therefore, an experiment that varies Y while holding X constant can indicate whether or not Y is involved in the rate-determining step. If the identity of Y has little effect on rate, then it must not be involved in the rate-determining step. Such experimental evidence can be taken as evidence of a dissociative mechanism. For example, the rate constants for reaction of \(\ce{[Cr(NH3)5H2O}]^3+}\) with different incoming ligands, shown below, has rate constants of similar magnitude (they are approximately within one order of magnitude), indicating a dissociatively activated mechanism. In this case, other lines of evidence suggest this is a reaction with a \(I_d\) mechanism.

\[\ce{[Cr(NH3)5H2O]^3+ + Y^{-} <=> [Cr(NH3)5Y]^2+ + H2O} \nonumber \]

Table \(\PageIndex{1}\): Rate Constants for Exchange of Aquo Ligand of pentaammineaquo chromium(III) ion by incoming ligand, Y (chemical equation shown above). There is little effect of the identity of the incoming ligand on the rate constant. This data was sourced from Miessler, Fischer and Tarr's Inorganic Chemistry, 5th edition, pg 449.

Entering Ligand, \(\ce{Y^-}\)	Rate Constant, \(k_1 \; (10^{-4}M^{-1}s^{-1})\)
\(\ce{NCS^-}\)	4.2
\(\ce{Cl^-}\)	0.7
\(\ce{Br^-}\)	3.7
\(\ce{CF3CO2^-}\)	1.4

2. Steric Crowding of the Metal Complex

Steric crowding of the metal complex would inhibit a dissociative pathway through steric crowding of the entering ligand. However, steric crowding can increase the stability of the intermediate after dissociation of the ligand from the crowded octahedral complex. If the reaction rate increases with steric crowding of the reactant complex, this is taken as evidence to support a dissociative mechanism.

3. Volume of Activation

One molecule generally takes up less space than two sperate molecules. This usually holds true in solution. Measurement of a rate constant's dependence on pressure can be used to determine the volume of activation (\(\Delta V_{act}\)) and give insight into the mechanism of that reaction. In a dissociation mechanism, the dissociation causes one metal complex to become two separate molecules. Thus, the intermediate should, in principle, take up more space than the reactant complex. In a situation like this, we expect that the rate of reaction should decrease with increasing pressure, giving a positive value for \(\Delta V_{act}\). However, solvation of ions can influence volume, and this should be considered in interpretation of pressure-dependence data.

4. Increased coulombic attraction with the leaving group decreases reaction rate.

Couloubic (electrostatic) attraction between the dissociating ligand, X, and the metal complex should slow ligand dissociation. Coulombic attraction increases with increased magnitude of charges and with decreased distance. If the reaction rate slows with increased charge of the metal ion or the ligand itself, this is taken as evidence of a dissociative mechanism. Likewise, if rate decreases as the radius of the central metal ion is decreased, this is evidence to support a dissociative mechanism.

5. Increased strength of the M-X bond decreases reaction rate.

Free energy relationships between the formation constant of M-X and the kinetic rate constant of the reaction can provide evidence to support a dissociative mechanism (Discussed in the next section).