11.2.1: Finding Microstates and Term Symbols

Constructing "Free Ion" Term Symbols and their Relative Energies

The different electronic states of an atom or ion are described by \(L\) and \(S\) in the form of a term symbol (Figure \(\PageIndex{1}\)). Keep in mind that \(M_l\) is related to \(L\), and \(M_s\) is related to \(S\), and in some cases their values are equal.

One term symbol can describe one or more microstates with the same energy. The free ion terms are useful in the interpretation of electronic spectra. These term symbols are also commonly called free ion terms (or Russell-Saunders terms) because they describe the atomic or ionic state, free of any ligands. The term symbol indicates the total orbital angular momentum of the atom, (\(L\)), and the multiplicity, \((2S+1)\), of the state. The multiplicity can be found with the formula, \((2S+1)\), but it is also equal to the number of unpaired electrons plus one.

\[\text{Multiplicity } = \left( 2S+1 \right) = \left( \text{# of unpaired electrons }+1 \right)\]

The generic form of a free ion term symbol is shown in Figure \(\PageIndex{1}\). Recall that \(L=0,1,2, 3...\) is denoted by a capital letter \(S, P, D, F...\), respectively. The latter designation for \(L\) is used in the term symbol.

Figure \(\PageIndex{1}\): A term symbol of the free ion takes the form \(^{(2S+1)}L\), where \(L\) is the total orbital angular momentum quantum number, and \(S\) is the total intrinsic spin quantum number. The value \(2S+1\) is called the multiplicity. (CC-BY-NC; Kathryn Haas)

Example 11.2.1.1 : Hydrogen Ground State

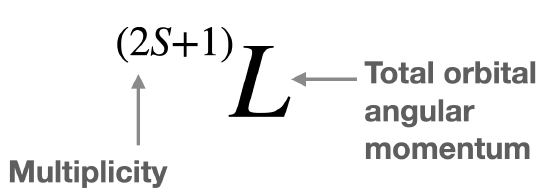
What is the free ion term symbol of an H atom in the ground state (\(1s^1\))? How many microstates are there for the ground state hydrogen atom? Comment on the degeneracy and multiplicity of the state.

Solution

There is only one electron in a \(s\) orbital. That electron must have \(l=0\), and \(s\) could be either \(+\frac{1}{2}\) or \(-\frac{1}{2}\). This is two possible microstates, one with spin "up" and one with spin "down". In either case there is only one value of the total intrinsic spin quantum number, \(S=+\frac{1}{2}\). Therefore, the only possible value of spin multiplicity is Multiplicity \(=2\times (+\frac{1}{2})+1 = 2\). The \(s\) orbital corresponds to \(l =0\), so \(L=0\), or \(S\). Thus the term symbol is \(^2S\).

There are two possible microstates of the ground state (both represented by the ground state term). One microstate has \(m_s=+\frac{1}{2}\) and the other has \(m_s=-\frac{1}{2}\).

The question about degeneracy specifically asks about degeneracy of the state. Let's give the most complete answer possible. In terms of energy levels (the ground state in this case), there are two microstates with approximately equal (degenerate) energy, thus the degeneracy of the state is two (2) and is the same as the multiplicity (\(2S+1=2\)). However, sometimes we also refer to the "degeneracy" of electron configurations. It is important to recognize that ground state electron configuration with \(M_s=m_s=+\frac{1}{2}\) is singly degenerate, and the same is true for \(M_s=m_s=-\frac{1}{2}\). Recognising degeneracy of electron configurations will be useful later in this chapter because the degeneracy of an electron configuration can be helpful for interpreting term symbols in an octahedral field.

Exercise \(\PageIndex{1}\)

Find the term symbols for the following cases:

1. \(L=0, \ S=0\)
2. \(L=0, \ S=\frac{1}{2}\)
3. \(L=1, \ S=1\)
4. \(L=2, \ S=\frac{3}{2}\)
5. \(L=3, \ S=2\)

Answer

(a) \(^1S\)
(b) \(^2S\)
(c) \(^3P\)
(d) \(^4D\)
(e) \(^5F\)

Finding all possible microstates for an atom or ion

What are the possible microstates and the overall number of microstates for a free ion with \(d^2\)-electron configuration? We can express this in a so-called microstate table (\(\PageIndex{2}\)).

Figure \(\PageIndex{2}\). \(d^2\) electron configuration microstate table. This table is organized with \(M_l\) values increasing horizontally and \(M_s\) values decreasing vertically. You may see different ways to organize a microstate table, and there is no wrong orientation to use, as long as you can use it to correctly find and organize microstates. Each microstate is indicating using notion \((m_l)^{m_s}\), where only the sign of \(m_s\) is indicated for simplicity. For example, an electron in \(m_l=-2\) with \(m_s=+\frac{1}{2}\) is notated \(-2^+\).

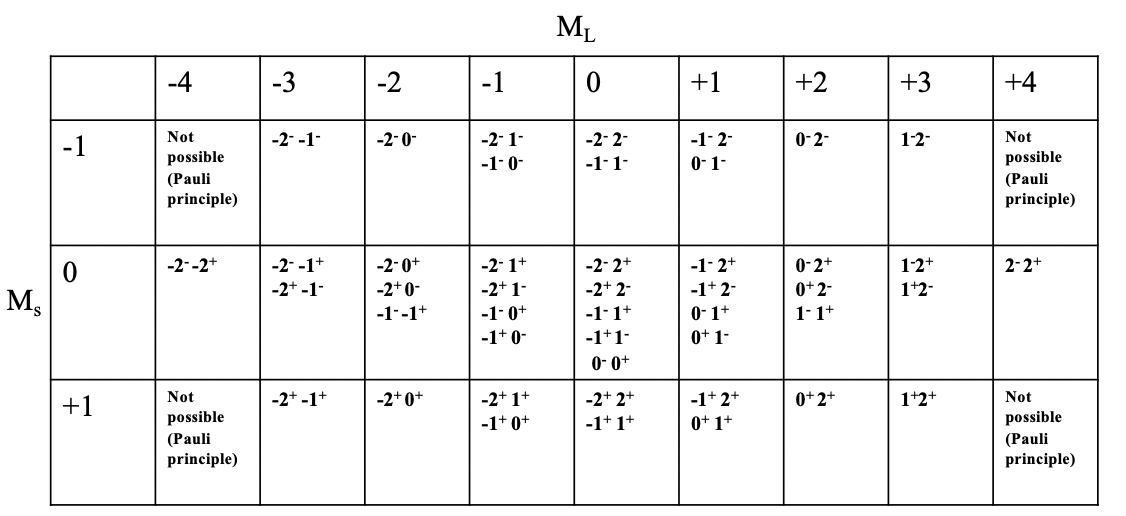
You can see the microstate table for the \(d^2\) electron configuration depicted above. Each column represents a possible value \(M_l\). For the \(d^2\) configuration, \(M_l\) can adopt values from -4 to +4, hence there there are 9 columns. Each row represents possible \(M_s\) value. For the \(d^2\) electron configuration, \(M_s\) can vary between +1 and -1. \(M_s=+1\) means both electrons have the spin \(+\frac{1}{2}\), \(M_s=0\) means one electron has the spin \(+\frac{1}{2}\) and the other one has the spin \(-\frac{1}{2}\). The \(M_s=-1\) value is adopted when both electrons have the spin \(-\frac{1}{2}\). Now we can combine each \(M_s\) value with each \(M_l\) value, which defines a particular field in the table. You can see that some fields are empty due to the Pauli principle. For example, the field for \(M_l=-4\) and \(M_s=-1\) is not filled because in this case both electrons would have the same quantum numbers, namely \(m_l=2\), and \(m_s=-\frac{1}{2}\). We can further see that for some fields only one combination of electrons is possible, while for others there are multiple possible microstates. For example, for the field with \(M_l=4\) and \(M_s=0\) there is only one combination of electrons possible. You can see the notation “\(2^- 2^+\)” in this field. This means that the first electron has an \(m_l\) value of 2 and a spin of \(-\frac{1}{2}\) and the second electron also has an \(m_l\) value of 2 and an \(m_s\) value of \(+\frac{1}{2}\). The most populated field is the field for \(M_l=0\) and \(M_s=0\); there are overall five microstates with that combination of \(M_l\) and \(M_s\) values. If we count the overall number of microstates in the table then we arrive at the number 45. This is consistent with what we would expect according to the following formula. \[\text{#microstates} = (2L+1)(2S+1)\]

In our example L=4 and S = 1, and thus the number of microstates is: \(((2x4)+1)((2x1)+1)=45\). In general for a \(d^n\) electron configuration with \(n\) d-electrons, the number of microstates is \((10!)/((10-n)!n!)\).

One useful property of a microstate table is that we can derive all possible terms and term symbols for a particular electron configuration from it. For simplification's sake, we indicate a possible microstate in the table in Figure \(\PageIndex{5}\) just by an “x”. Then we draw the largest possible rectangular box into the microstate table that contains only fields with at least one possible electron combination (Figure \(\PageIndex{5}\)).

Figure \(\PageIndex{5}\). Deriving the terms and term symbols for the \(d^2\) electron configuration from the microstate table

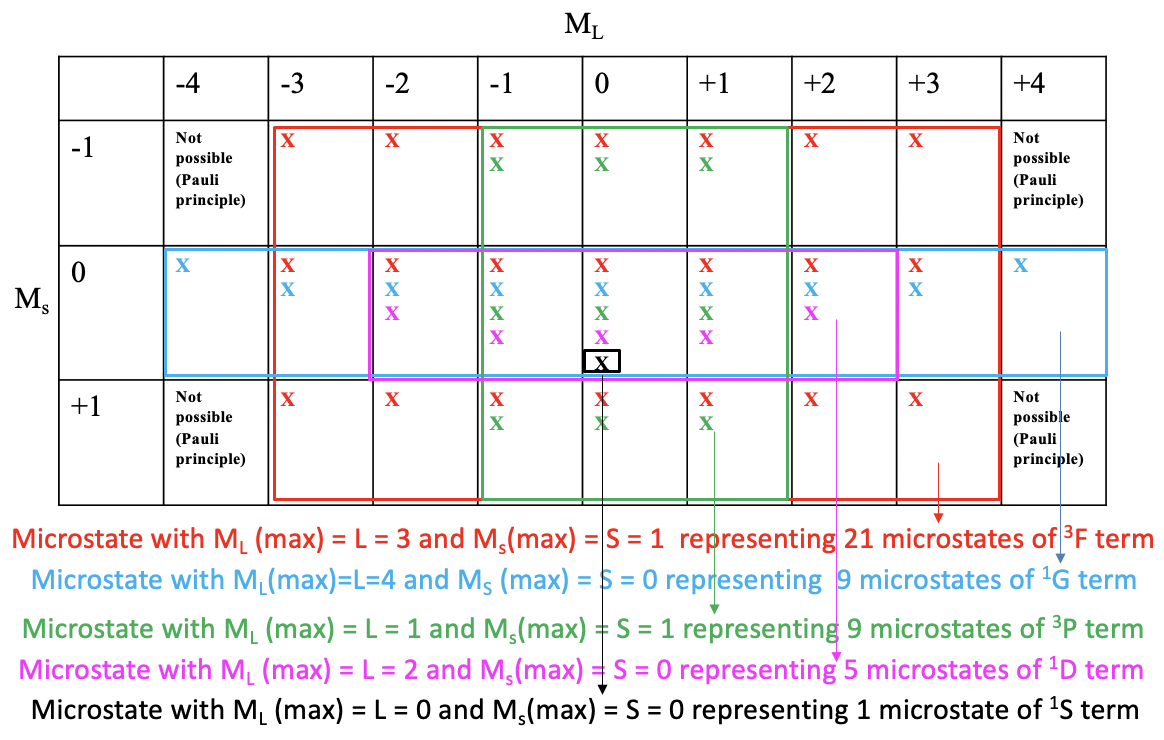
You can see that the largest possible box is the red box drawn (Figure \(\PageIndex{5}\)). This box contains the microstates that belong to the first term of the electron configuration \(d^2\). The number of microstates is equal to the number of fields within the red box. That makes \(7\times 3=21\) microstates. What is the term symbol for this term? In order to answer this question we need to find the microstate in the red box that has the highest \(M_l\) and the highest \(M_s\) value. You can see that it is the one with \(M_l=3\) and \(M_s=2\). Thus, L=3 and S=1. This defines the term as a ³F term because 2S+1 = 3, and L=3 corresponds to the term symbol F. This term is a triplet term. Note that a triplet term also includes microstates with opposite spins. Overall seven of the 21 microstates have \(M_s=0\).

Next, we look what is the next-largest rectangular box we can draw, and which contains microstates we did not consider yet. We can see that the blue box contains nine fields equaling nine microstates. The microstate within this box that has the highest \(M_l\) and \(M_s\) values is the one with \(M_l=4\) and \(M_s=0\). This defines a ¹G term. This is a singlet term. Note that a singlet term ONLY has microstates with paired spins (M_s=0).

There is another rectangular box which also contains nine microstates. It is the green one. The microstate with the highest \(M_l\) and \(M_s\) values is the one with \(M_l=1\) and \(M_s=1\). Thus, \(L =1\), and \(2S+1=3\), which defines a \(^3P\) term. Note that despite this being a triplet term, which indicates two unpaired electrons (\S=1\), the term also contains three microstates that have opposite spins with a total \(M_s=0\).

The next-largest box is the purple one containing five fields and five microstates. What is the term with the highest \(M_l\) and \(M_s\) values? It is the one with \(M_l=2\) and \(M_s=0\). This means that L=2 and S=0, which defines a ¹D term, a singlet term with only microstates with paired spins. There is one microstate left that we did not consider thus far, the one with \(M_l=0\) and \(M_s=0\). These are the highest \(M_l\) and \(M_s\) values because there is no other microstate. Thus, this term contains only one microstate and the term symbol is \(^1S\). Now we have found all the terms and term symbols.

Example 11.2.1.2 : Boron

What are the possible term symbols for \(1s^2 2s^2 2p^1\) electronic configuration of boron? Which is the ground state?

Solution

We only need to consider the one electron in the \(2p\) orbital, since that is the only open shell electron. For one electron, there is only one value of \(S = ½\), so multiplicity must be \(2S+1=2\). The possible values of \(L\) for one electron in a \(p\) orbital are \(L=0,1\) (or S, and P terms). This gives the free ion term symbols \(^2P\) and \(^2S\). Both of these terms have multiplicity of 2, so the ground state would be the one with the highest value for \(L\). The ground state term is \(^2P\).

Example 11.2.1.3 : Beryllium Excited State

What are the term symbols for the \(1s^2 2s^1 2p^1\) excited-state electronic configuration of Beryllium?

Solution

The term symbols will be of the form \(^1P\) and \(^3P\). For the \(^1 P\) state, \(L=1\) and \(S=0\), so the total angular momentum \(J=1\). For the second state, \(L=1\) and \(S=1\), so the possible values of \(J=2,1,0\). There are four microstates for this configuration with term symbols of \(^1 P_1\) and \(^3 P_2\), \(^3P_1\), and \(^3P_0\).

Finding The Ground State Term

...from a list of microstates

Each term symbol represents an atomic state with an associated energy level. If you have found all the possible microstates using a microstate table, and have identified their terms, then the term with the lowest energy (ie the ground state) can be found using Hund's first two rules. In abbreviated form, Hund's rules state...

1. The lowest energy electron configuration has the maximum multiplicity (the maximum number of unpaired electrons).
2. For a given multiplicity, the configuration with the largest total orbital angular momentum (\(L\)) value has the lowest energy.

In the case of the \(p^2\) carbon atom (see Figure \(\PageIndex{1}\)), the lowest energy state would have a multiplicity of 3 (two unpaired electrons). Of the states with a multiplicity of 3, the largest value of \(L\) is 1 (and thus, \(P\)). Thus, the ground state term for carbon is \(^3P\). These rules are reliable for identifying the ground state term for any atom, but have limited use for ordering relative energies outside of the ground state for 3d metal ions and other light atoms. For heavier atoms (e.g., 4d metals) another type of interaction, called jj coupling must be considered, but this is outside the scope of this discussion. Tip: There is a deep symmetry that connects different electronic configurations. It turns out that a \(p^1\) configuration has the same term symbols as a \(p^5\). Similarly, \(p^2 = p^4\). A similar relationship can be used to figure out high electron number term symbols for the \(d\) and \(f\) orbitals.

...if you just want the find Ground State term

To assign transitions in an electronic spectrum, we should know the ground state term, as well as all other terms and their relative energies for a given atom or ion. However, the identification of all possible terms becomes tedious with more than one or two electrons in the \(d\) orbitals. Fortunately, there are tools (like correlation diagrams) that can help us find all terms for an atom or ion, as long as the ground state term can be identified. Here is a quick shortcut for finding the ground state term for transition metal complex with partially-filled \(d\) shell.

Quickly find the ground state free ion tern

In this case, we'll focus on transition metal d-orbitals. To begin, you'll need to know the metal ion identity and its oxidation state. These instructions assume that the \(d\) orbital is the only shell that is partially filled.

1. Determine the number of d-electrons.
2. Then fill these electrons into an electron orbital diagram of five degenerate orbitals, putting electrons into the highest value of \(m_l\) first, and filling orbitals with single electrons before pairing them (just as you may have done in an introductory chemistry course).
3. Calcuate the total intrinsic spin (\S\) and spin multiplicity using the diagram drawn in #2.
4. Calculate \(L\) using the diagram drawn from #2.
5. Write the term symbol for the ground state.

Let's use the example of the \(\ce{[Cr(NH3)6]^3+}\) complex ion, and determine its ground state term following the shortcut described above.

1. Determine the number of \(d\)-electrons.
   \(\ce{[Cr(NH3)6]^3+}\) contains \(\ce{Cr^3+}\), which is a \(d^3\) metal ion. There are three \(d\) electrons.
2. Draw a diagram of five degenerate \(d\) orbitals, with \(m_l\) values labeled. Fill in the electrons to maximize \(m_s\) and \(m_l\).
   
3. Calculate spin multiplicity (should be the maximum possible value!).
   \(S= m_{s_1} + m_{s_2} + m_{s_3} = +\frac{1}{2} + +\frac{1}{2} + +\frac{1}{2} = \frac{3}{2}\)
   Spin multiplicity = \(2S+1 = 2 \frac{3}{2} + 1 = 4\)
4. Calculate \(L\) (should be the maximum possible value after spin is maximized.
   \(L = m_{l_1}+ m_{l_2} + m_{l_3} = 2 + 1 + 0 = 3\)
5. Write the ground state free ion term:
   \(^{(2S+1)}L = \; ^4F\)

Exercise \(\PageIndex{2}\)

Earlier on this page, you found all the terms for a \(d^2\) metal ion. Use both of the methods (Hund's rule, and the shortcut method) described here to identify the ground state term for \(d^2\).

Answer

Using Hund's rule: The terms identified for \(d^2\) are \(^3F, \; ^1G, \; ^3P, \; ^1D,\) and \(^1S\). Hund's first rule tells us that either \(^3F\) or \(^3P\) could be the ground state because these two terms have the highest multiplicity. Hund's second rule tells us that \(^3F\) must be the ground state because it has the largest value of \(L\).

Using the shortcut: The drawing is shown below, with one electron in \(m_l=+2\) and the second electron in \(m_l=+1\). Both electrons are unpaired with \(m_s=+\frac{1}{2}\). This gives \(L=3\) or an F term. And, \(S=1\) with a multiplicity of 3. The ground state term is \(^3F\).

Exercise \(\PageIndex{3}\)

Find the ground state free ion terms for the metal ions in the following cases:

(a) \(\ce{[Ti(H2O)6]Cl2}\)

(b) \(\ce{[Ti(NH3)6]Cl3}\)

(c) \(\ce{[Cu(H2O)6]Cl2}\)

Answer

(a) \(\ce{Ti^2+}\) is a \(d^2\) metal ion, \(^3F\)

(b) \(\ce{Ti^3+}\) is a \(d^1\) metal ion, \(^2D\)

(c) \(\ce{Cu^1+}\) is a \(d^9\) metal ion, \(^2D\). Note that \(d^9\) and \(d^1\) are related by the symmetry of their electronic states.