9.2: History
- Page ID
- 151408
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)History of the Coordination Compounds
Coordination compounds have been known and used since antiquity; one of the oldest synthetic pigments is the blue pigment Egyptian blue, a copper complex of formula CaCuSi4O10 used by the Egyptians since the third Millenium B.C. (in ancient China the Ba analogue, Han blue, was discovered independently). The blue color of Egyptian blue is due to interlocked Cu(Si2O7)4 units in which each copper is coordinated by four O atoms in a square planar arrangement. Later, in 1706, the Berlin painter Diesbach would discover another deep blue pigment, Prussian blue: \(\ce{KFe2(CN)6}\).
Despite their long use, the chemical nature of coordination compounds was unclear for a number of reasons. For example, many compounds called “double salts” were known, such as \(\ce{AlF3·3KF}\), \(\ce{Fe(CN)2·4KCN}\), and \(\ce{ZnCl2·2CsCl}\), which were combinations of simple salts in fixed and apparently arbitrary ratios. Why should \(\ce{AlF3·3KF}\) exist but not \(\ce{AlF3·4KF}\) or \(\ce{AlF3·2KF}\)? And why should a 3:1 KF:\(\ce{AlF3}\) mixture have different chemical and physical properties than either of its components? Similarly, adducts of metal salts with neutral molecules such as ammonia were also known—for example, \(\ce{CoCl3·6NH3}\), which was first prepared sometime before 1798. Like the double salts, the compositions of these adducts exhibited fixed and apparently arbitrary ratios of the components. For example, \(\ce{CoCl3·6NH3}\), \(\ce{CoCl3·5NH3}\), \(\ce{CoCl3·4NH3}\), and \(\ce{CoCl3·3NH3}\) were all known and had very different properties, but despite all attempts, chemists could not prepare \(\ce{CoCl3·2NH3}\) or \(\ce{CoCl3·NH3}\).
Although the chemical composition of such compounds was readily established by existing analytical methods, their chemical nature was puzzling and highly controversial. The major problem was that what we now call valence (i.e., the oxidation state) and coordination number were thought to be identical. As a result, highly implausible (to modern eyes at least) structures were proposed for such compounds. Of these the most influential was the Blomstrand-Jørgensen chain theory of bonding in coordination compounds, which predicted the “Chattanooga choo-choo” model for CoCl3·4NH3 shown in Scheme \(\sf{\PageIndex{I}}\).
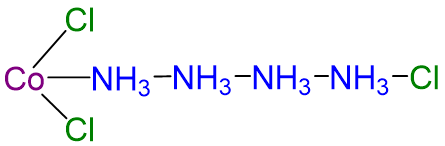
Nevertheless, this theory was not wholly illogical and, in fact, explained much of the analytical data on coordination compounds available to chemists of the time. This data included the electrical conductivity of aqueous solutions of these compounds, which was roughly proportional to the number of ions formed per mole, and the number of free chloride ions present, which could be determined by precipitating them gravimetrically as AgCl. In the case of CoCl3·4NH3, two ions and one chloride were produced when the compound was dissolved in water, which Jørgensen was able to explain using the chain structure shown above by postulating that chlorides attached to NH3 could dissociate while those attached to Co could not. The modern theory of coordination chemistry, which overthrew the chain theory, is based largely on the work of Alfred Werner (1866–1919; Nobel Prize in Chemistry in 1913). In a series of careful experiments carried out in the late 1880s and early 1890s, he examined the properties of several series of metal halide complexes with ammonia. For example, five different “adducts” of ammonia with PtCl4 were known at the time: PtCl4·nNH3 (n = 2–6). Some of Werner’s original data on these compounds are shown in Table \(\PageIndex{1}\). Werner’s data on PtCl4·6NH3 in Table \(\PageIndex{1}\) showed that all the chloride ions were present as free chloride. In contrast, PtCl4·2NH3, was a neutral molecule that did not give free chloride ions when dissolved in water.
Werner, the son of a factory worker, was born in Alsace. He developed an interest in chemistry at an early age, and he did his first independent research experiments at age 18. While doing his military service in southern Germany, he attended a series of chemistry lectures, and he subsequently received his PhD at the University of Zurich in Switzerland, where he was appointed professor of chemistry at age 29. He won the Nobel Prize in Chemistry in 1913 for his work on coordination compounds, which he performed as a graduate student and first presented at age 26. Apparently, Werner was so obsessed with solving the riddle of the structure of coordination compounds that his brain continued to work on the problem even while he was asleep. In 1891, when he was only 25, he woke up in the middle of the night and, in only a few hours, had laid the foundation for modern coordination chemistry.
| Complex | Conductivity (ohm−1) | Number of Ions per Formula Unit | Number of Cl− Ions Precipitated by Ag+ |
|---|---|---|---|
| PtCl4·6NH3 | 523 | 5 | 4 |
| PtCl4·5NH3 | 404 | 4 | 3 |
| PtCl4·4NH3 | 299 | 3 | 2 |
| PtCl4·3NH3 | 97 | 2 | 1 |
| PtCl4·2NH3 | 0 | 0 | 0 |
These data led Werner to postulate that metal ions have two different kinds of valence: (1) a primary valence (oxidation state) that corresponds to the positive charge on the metal ion and (2) a secondary valence (coordination number) that is the total number of ligands bound to the metal ion. If Pt had a primary valence of 4 and a secondary valence of 6, Werner could explain the properties of the PtCl4·NH3 adducts by the following reactions, where the metal complex is enclosed in square brackets:
\[\begin{align} \mathrm{[Pt(NH_3)_6]Cl_4} &\rightarrow \mathrm{[Pt(NH_3)_6]^{4+}(aq)+4Cl^-(aq)} \\[4pt]
\mathrm{[Pt(NH_3)_5Cl]Cl_3} &\rightarrow \mathrm{[Pt(NH_3)_5Cl]^{3+}(aq) +3Cl^-(aq)}\\[4pt]
\mathrm{[Pt(NH_3)_4Cl_2]Cl_2} &\rightarrow \mathrm{[Pt(NH_3)_4Cl_2]^{2+}(aq) +2Cl^-(aq)}\\[4pt]
\mathrm{[Pt(NH_3)_3Cl_3]Cl} &\rightarrow \mathrm{[Pt(NH_3)_3Cl_3]^+(aq) + Cl^-(aq)}\\[4pt]
\mathrm{[Pt(NH_3)_2Cl_4]} &\rightarrow \mathrm{[Pt(NH_3)_2Cl_4]^0(aq)} \end{align} \nonumber \]
Further work showed that the two missing members of the series—[Pt(NH3)Cl5]− and [PtCl6]2−—could be prepared as their mono- and dipotassium salts, respectively. Similar studies established coordination numbers of 6 for Co3+ and Cr3+ and 4 for Pt2+ and Pd2+.
The series CoCl3·xNH3 was particularly important in establishing the correctness of Werner's coordination theory over the rival chain theory. By ~1900 conductivity measurements suggested that the members of the series gave the number of ions shown in Table \(\sf{\PageIndex{1}}\).
| Compound | Color | Werner formulation | Blomstrand-Jørgensen chain theory formulation | Number of ions in solution |
|---|---|---|---|---|
| CoCl3·6NH3 | yellow | [Co(NH3)6]Cl3 | 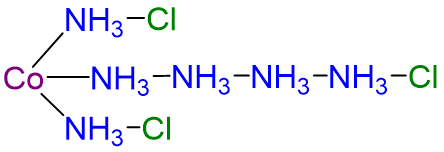 |
4 |
| CoCl3·5NH3 | violet | [Co(NH3)5Cl]Cl2 | 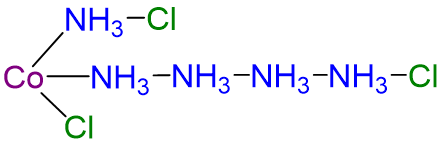 |
3 |
| CoCl3·4NH3 | green | [Co(NH3)4Cl2]Cl | 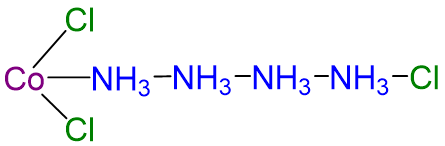 |
2 |
| CoCl3·3NH3 | orange | [Co(NH3)4Cl3] | 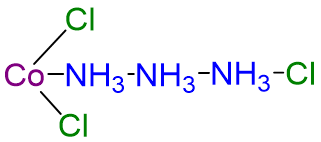 |
0 |
What does this data suggest about the relative explanatory power of Werner's coordination theory and chain theory? Explain.
- Answer
-
Remember that
- chain theory predicts that the number of ions is the number formed when the Cl atoms bound in a chain with NH3 dissociate.
- coordination theory predicts the number of ions based on the number of complex ions and their counterions.
Based on this the predictions of coordination theory and chain theory can be compared with the experimental data, as is done in Table \(\sf{\PageIndex{2}}\).
Table \(\sf{\PageIndex{2}}\): Comparison of ions predicted for the CoCl3·xNH3 series by coordination theory and chain theory with the number observed experimentally. Compound Color Ions predicted by Werner's coordination theory Number of ions predicted by coordination theory Ions predicted by Blomstrand-Jørgensen chain theory Number of ions predicted by chain theory Observed Number of ions in solution CoCl3·6NH3 yellow [Co(NH3)6]3+
Cl-
Cl-
Cl-
4 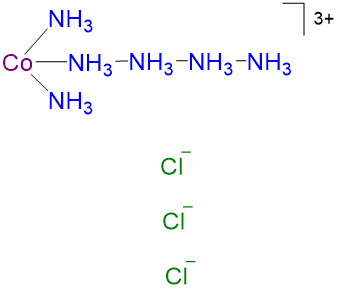
4 4 CoCl3·5NH3 violet [Co(NH3)5Cl]2+
Cl-
Cl-
3 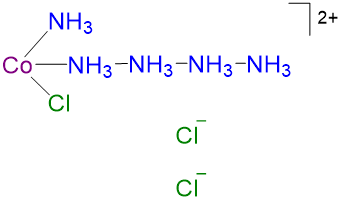
3 3 CoCl3·4NH3 green [Co(NH3)4Cl2]+
Cl-
2 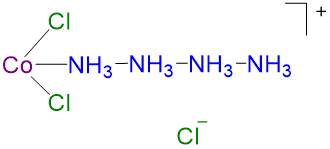
2 2 CoCl3·3NH3 orange None 0 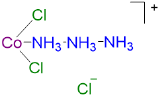
2 0 - As can be seen by comparing the number of ions predicted by coordination and chain theory in Table \(\sf{\PageIndex{2}}\), coordination theory successfully explains all the observed ion counts, while chain theory fails to explain the lack of ions observed for CoCl3·3NH3.
- Nevertheless, as is often the case when developing theoretical models using data from real experimental investigations, these observations did not convince Jørgensen, who could point to the experimental difficulty of determining the number of ions present from solution conductivity data.
What ultimately convinced Jørgensen of the correctness of Werner's coordination model over his own chain theory was how Werner's explanation of the structure of cobalt coordination complexes using an octahedral coordination geometry explained the existence of isomers in Co complexes containing Cl and NH3 ligands. In the case of [Co(NH3)4Cl2]Cl two isomers were known: one red and the other green. Because both compounds had the same chemical composition and the same number of groups of the same kind attached to the same metal, there had to be something different about the arrangement of the ligands around the metal ion. Werner’s key insight was that the six ligands in [Co(NH3)4Cl2]Cl had to be arranged at the vertices of an octahedron because that was the only structure consistent with the existence of two, and only two, stereoisomers (Figure \(\PageIndex{1}\)). His conclusion was also corroborated by the existence of two and only two stereoisomers of the next compound in the series: Co(NH3)3Cl3.
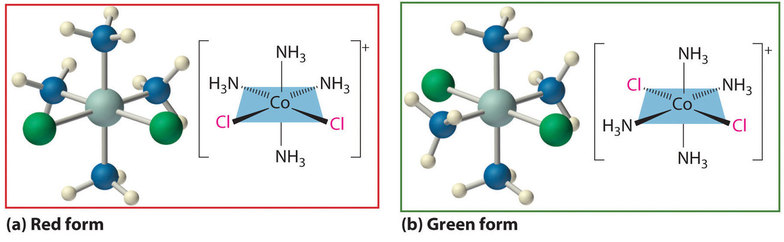
In Werner’s time, many complexes of the general formula MA4B2 were known, but no more than two different compounds with the same composition had been prepared for any metal. To confirm Werner’s reasoning that this suggests these complexes possess an octahedral geometry, calculate the maximum number of different structures possible for six-coordinate MA4B2 complexes with each of the three most symmetrical possible structures the ligands will form about the central metal - a hexagon, a trigonal prism, and an octahedron.
Assuming that the absence of evidence for additional compounds in this case serves as reasonable circumstantial evidence for their absence, what does the fact that no more than two forms of any MA4B2 complex were known suggest about the three-dimensional structures of these complexes?
Solution
In this problem you are given
- the stochiometry of the complexes, MA4B2
- three possible coordination geometries - hexagonal, trigonal prismatic, and octahedral.
In order to calculate the number of isomers that could be present for each geometry it is best to follow a systematic approach. Since there are fewer B type ligands than A type ligands, the easiest way to do this for each geometry is to start by placing a B ligand at one vertex and then to determine how many different positions are available for the second B ligand.
The three regular six-coordinate structures are shown here, with each coordination position numbered so that we can keep track of the different arrangements of ligands. For each structure, all vertices are equivalent. We begin with a symmetrical MA6 complex and simply replace two of the A ligands in each structure to give an MA4B2 complex:
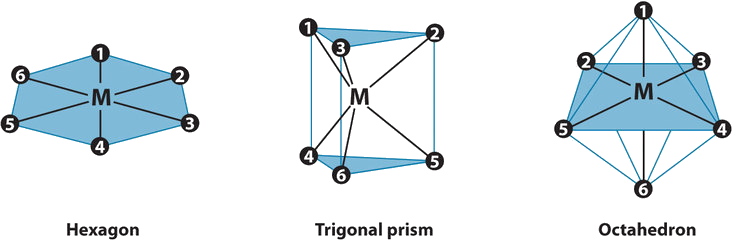
For the hexagon, we place the first B ligand at position 1. There are now three possible places for the second B ligand:
- position 2 (or 6)
- position 3 (or 5)
- position 4
The (1, 2) and (1, 6) arrangements are chemically identical because the two B ligands are adjacent to each other. The (1, 3) and (1, 5) arrangements are also identical because in both cases the two B ligands are separated by an A ligand. Those of you who remember your ogranic chemistry might recognize that this situation is formally analogous to the ortho-, meta-, and para- isomerism in disubstituted benzenes.
Turning to the trigonal prism, we place the first B ligand at position 1. Again, there are three possible choices for the second B ligand:
- at position 2 or 3 on the same triangular face
- position 4 (on the other triangular face but adjacent to 1)
- position 5 or 6 (on the other triangular face but not adjacent to 1).
The (1, 2) and (1, 3) arrangements are chemically identical, as are the (1, 5) and (1, 6) arrangements.
In the octahedron, however, if we place the first B ligand at position 1, then we have only two choices for the second B ligand:
- position 2 (or 3 or 4 or 5)
- position 6.
In the latter, the two B ligands are at opposite vertices of the octahedron, with the metal lying directly between them. Although there are four possible arrangements for the former, they are chemically identical because in all cases the two B ligands are adjacent to each other.
The number of possible MA4B2 arrangements for the three geometries is thus: hexagon, 3; trigonal prism, 3; and octahedron, 2. The fact that only two different forms were known for all MA4B2 complexes that had been prepared suggested that the correct structure was the octahedron but did not prove it. For some reason one of the three arrangements possible for the other two structures could have been less stable or harder to prepare and had simply not yet been synthesized. When combined with analogous results for other types of complexes (e.g., MA3B3), however, the data were best explained by an octahedral structure for six-coordinate metal complexes.
Determine the maximum number of structures that are possible for a four-coordinate MA2B2 complex with either a square planar or a tetrahedral symmetrical structure.
- Answer
-
square planar, 2; tetrahedral, 1
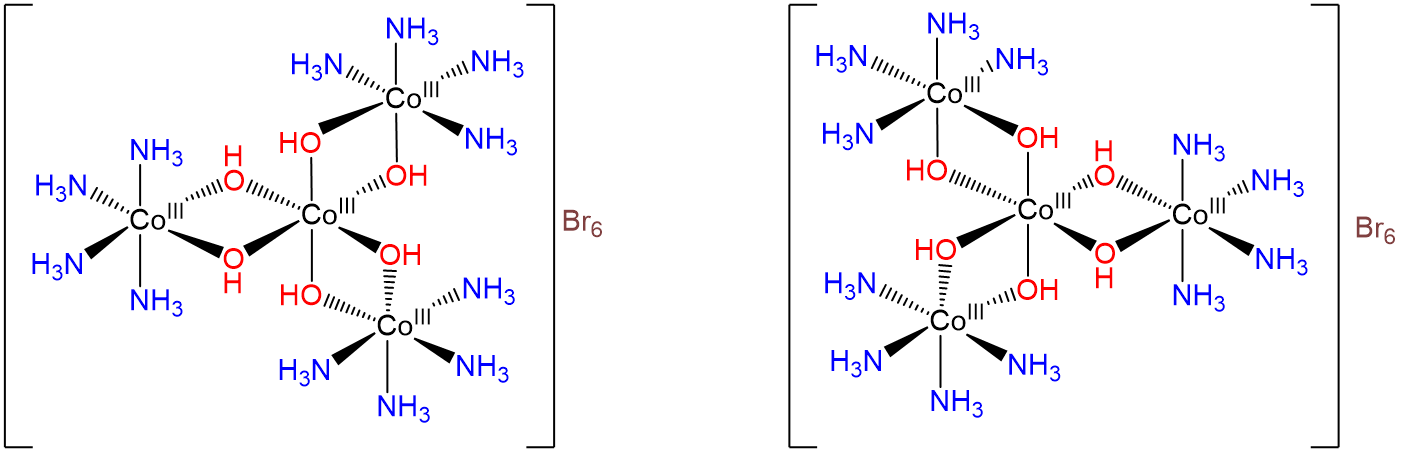
Even Werner's explanation of isomerism in coordination complexes in terms of octahedral and other recognized coordination geometries did not convince all chemists until he was able to resolve a racemic mixture of d- and l-[Co{Co(NH3)4(OH)2}3] into its enantiomers, which are shown in Scheme \(\sf{\PageIndex{II}}\). By doing so Werner demonstrated to chemists of his time (virtually none of whom knew group theory) that tetrahedral carbon atoms were not required for chirality; D3 octahedral complexes were also chiral.