8.1.4: As may be seen from considering an element's redox diagrams, main group elements (aside from the noble gases) generally are more oxidizing towards the upper left of the periodic table and more reducing towards the lower right of the periodic table
- Page ID
- 199663
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The existence of diagonal relationships among elements in the periodic table and the unique properties of the first and second row elements have already been discussed. Thus before beginning a survey of the descriptive chemistry of the elements, it only remains to describe the general trends associated with the redox properties of the elements and to present several conceptual and graphical tools that make it possible to rapidly grasp the general features of the redox chemistry of each element. These are the subject of the present section.
Elements on the left of the periodic table tend to act as reductants; those on the right as oxidants
The ability of the elements to act as oxidants and reductants is usually described by citing the reduction potentials associated with the reactions they undergo in solution. Thus before considering trends in the redox properties of the main group elements, this section will begin by pointing out how redox potentials work and what they represent.
Substances' standard reduction potentials describe the thermodynamic propensity of a substance to undergo reduction.
Redox potentials represent the thermodynamic potential for the substance to undergo reduction relative to the ideal standard hydrogen electrode (SHE).
\[2H^+(aq) + 2e^- \rightarrow H_2(g) ~~~~ E^{\circ} = 0.00V \nonumber \]
The ability of a substance to act as an oxidant or reductant is described by the relevant standard reduction potential. These correspond to reactions of the form
\[ \sf{\underset{reductant}{{substance}_{ox}(solv)} ~~+~~} ne^- \rightarrow \underset{oxidant}{{substance}_{red}(solv)} \nonumber \]
There are three things to notice about these standard reduction potentials.
1. Standard reduction potentials always corresponds to reduction of an oxidant to give a reductant. Consequently,
- thermodynamically better oxidants have more positive standard reduction potentials
- thermodynamically better reductants correspond to the products of standard reduction reactions with more negative standard reduction potentials (Figure \{\PageIndex{1}\).
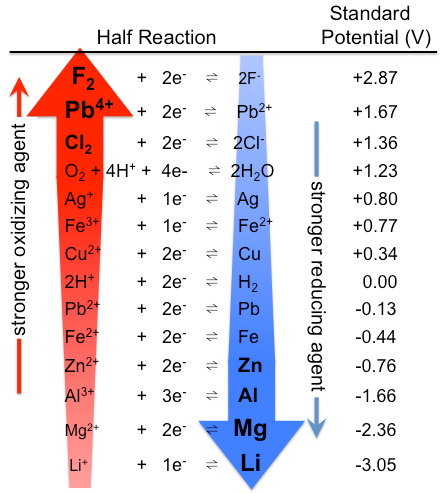
2. Since \(\Delta G^{\circ} = -nFE^{\circ}\), standard reduction potentials are a measure of the thermodynamic spontaneity of a reduction relative to the oxidation of H2(g). As such, reduction potentials are useful for determining whether a reaction can occur but are not useful for determining whether a reaction actually will occur under a given set of conditions. The kinetics of the reduction should also be considered. For instance, thermodynamically nitrate is a powerful oxidant in aqueous solution:
\[2NO_3^-(aq) + 12H^+ + 10e^- \rightarrow N_2(g) + 6H_2O(l) ~~~~E^{\circ} = 6.229 V! \nonumber \]
However, in solution there is a large kinetic barrier for nitrate reduction, and nitrate usually functions as an inert spectator ion even when strong reductants are present.
3. Since reduction potentials are thermodynamic quantities, they depend on the stability of both their oxidized and reduced forms. For reactions involving soluble species in solution, these stabilities in turn depend on the energy of solvation of any solution phase species involved. For this reason, there is no such thing as the potential of a given substance to act as an oxidant or reductant. They should always be specified relative to a given set of conditions.
Most tabulated redox potentials correspond to oxidations and reductions taking place in aqueous solutions. Moreover, for reactions involving the gain or loss of protons (or OH-), they likely correspond to reactions taking place in 1.0 M H+ solution (or, less commonly, 1.0 M OH-). Such potentials may not correspond closely to those taking place in nonaqueous solvents or in water at other pH values. Nevertheless, with these caveats it is possible to recognize rough trends in the redox properties of the elements.
There are three trends in the redox properties of the elements
The redox properties of the elements very roughly follow three general trends:
1. The noble gases are inert and as elements tend not to act as good oxidants or reductants
Otherwise
2. As one moves towards the left of the periodic table, elements tend to act as good reductants, while those towards the right tend to act as increasingly good oxidants.
3. As one moves down a group of the periodic table, elements tend to act as either weaker oxidants or better reductants.
These trends are summarized in Figure \(\PageIndex{2}\).
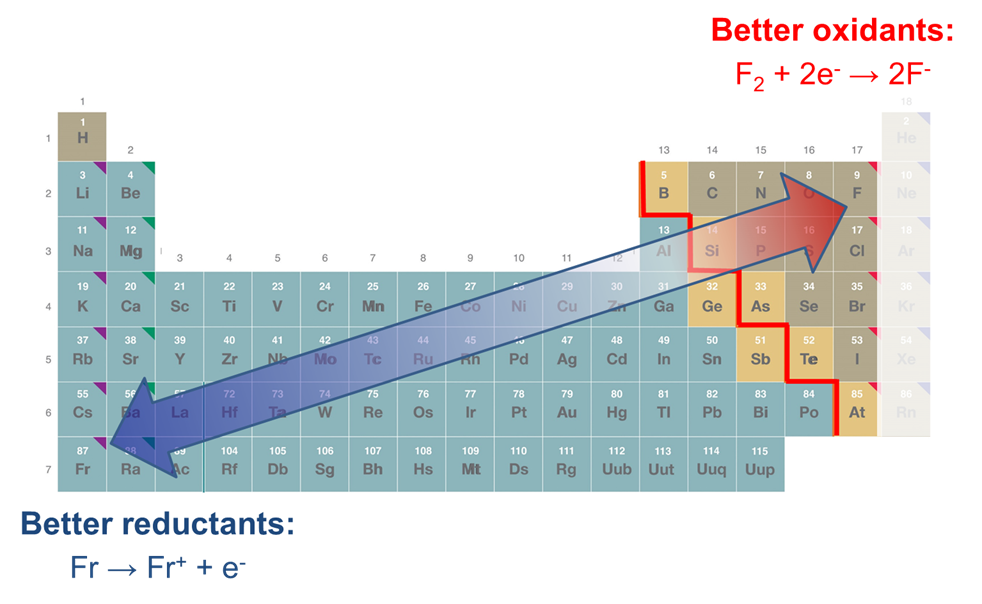
Since substances' ability to act as oxidants and reductants also depends on the stability of their oxidation and reduction products, these trends should be regarded as at best approximate. As can be seen from the data given in Table \(\PageIndex{1}\), the alkali metals furnish an important exception to the general trend that substances become more reducing towards the lower left of the periodic table. Among the elements included,2 lithium and not cesium is the most powerful reducing agent due to the high stability of the lithium cation in aqueous solution (anomalously high hydration energy). Further, from the potentials given in Table \(\PageIndex{1}\), it can also be seen that on going from K+ to Rb+ and Cs+ the reduction potentials do not decrease but instead remain approximately constant. In this case the decrease in ionization energy throughout this series is compensated for by a set of similar factors.3
Table \(\PageIndex{1}\) . Standard reduction potentials of aqueous alkali metal cations.
| Reduction | \(E^{\circ}\) |
| Li+(aq) + e- \(\rightarrow\) Li(s) | -3.040 |
| Na+(aq) + e- \(\rightarrow\) Na(s) | -2.713 |
| K+(aq) + e- \(\rightarrow\) K(s) | -2.924 |
| Rb+(aq) + e- \(\rightarrow\) Rb(s) | -2.924 |
| Cs+(aq) + e- \(\rightarrow\) Cs(s) | -2.923 |
Not only are there exceptions to the general trends in the redox properties of the free elements, but many elements also exhibit a rich and interesting redox chemistry involving the interconversion of multiple species possessing different oxidation states. In order to make sense of these it will be helpful to make use of the schematic and graphical tools that will be developed in the next sections.
References and notes
Unless otherwise noted all reduction potentials are taken from reference 1.
1. Bard, A. J.; Parsons, R.; Jordan, J. Standard potentials in aqueous solution. M. Dekker: New York, 1985.
2. Francium is not included because it is an unstable element and its reduction potential is not known.
3. These factors are beyond the scope of the present section but involve changes in the difference between a metal's cohesion free energy and the hydration free energy of its monocation.
Contributors and Attributions
Stephen Contakes, Westmont College

