Comparing Strengths of Oxidants and Reductants
- Page ID
- 6483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify how to view Standard Reduction Potentials from the perspective of viable reducing and oxidizing agents in REDOX reactions.
We can measure the standard potentials for a wide variety of chemical substances, some of which are listed in Table P2. These data allow us to compare the oxidative and reductive strengths of a variety of substances. The half-reaction for the standard hydrogen electrode (SHE) lies more than halfway down the list in Table \(\PageIndex{1}\). All reactants that lie below the SHE in the table are stronger oxidants than H+, and all those that lie above the SHE are weaker. The strongest oxidant in the table is F2, with a standard electrode potential of 2.87 V. This high value is consistent with the high electronegativity of fluorine and tells us that fluorine has a stronger tendency to accept electrons (it is a stronger oxidant) than any other element.
| Half-Reaction | E° (V) |
|---|---|
| Li+(aq) + e− \(\rightleftharpoons\) Li(s) | –3.040 |
| Be2+(aq) + 2e− \(\rightleftharpoons\) Be(s) | –1.99 |
| Al3+(aq) + 3e− \(\rightleftharpoons\) Al(s) | –1.676 |
| Zn2+(aq) + 2e− \(\rightleftharpoons\) Zn(s) | –0.7618 |
| Ag2S(s) + 2e− \(\rightleftharpoons\) 2Ag(s) + S2−(aq) | –0.71 |
| Fe2+(aq) + 2e− \(\rightleftharpoons\) Fe(s) | –0.44 |
| Cr3+(aq) + e− \(\rightleftharpoons\) Cr2+(aq) | –0.424 |
| Cd2+(aq) + 2e− \(\rightleftharpoons\) Cd(s) | –0.4030 |
| PbSO4(s) + 2e− \(\rightleftharpoons\) Pb(s) + SO42−(aq) | –0.356 |
| Ni2+(aq) + 2e− \(\rightleftharpoons\) Ni(s) | –0.257 |
| 2SO42−(aq) + 4H+(aq) + 2e− \(\rightleftharpoons\) S2O62−(aq) + 2H2O(l) | –0.25 |
| Sn2+(aq) + 2e− \(\rightleftharpoons\) Sn(s) | −0.14 |
| 2H+(aq) + 2e− \(\rightleftharpoons\) H2(g) | 0.00 |
| Sn4+(aq) + 2e− \(\rightleftharpoons\) Sn2+(aq) | 0.154 |
| Cu2+(aq) + e− \(\rightleftharpoons\) Cu+(aq) | 0.159 |
| AgCl(s) + e− \(\rightleftharpoons\) Ag(s) + Cl−(aq) | 0.2223 |
| Cu2+(aq) + 2e− \(\rightleftharpoons\) Cu(s) | 0.3419 |
| O2(g) + 2H2O(l) + 4e− \(\rightleftharpoons\) 4OH−(aq) | 0.401 |
| H2SO3(aq) + 4H+(aq) + 4e− \(\rightleftharpoons\) S(s) + 3H2O(l) | 0.45 |
| I2(s) + 2e− \(\rightleftharpoons\) 2I−(aq) | 0.5355 |
| MnO42−(aq) + 2H2O(l) + 2e− \(\rightleftharpoons\) MnO2(s) + 4OH−(aq) | 0.60 |
| O2(g) + 2H+(aq) + 2e− \(\rightleftharpoons\) H2O2(aq) | 0.695 |
| H2SeO3(aq) + 4H+ + 4e− \(\rightleftharpoons\) Se(s) + 3H2O(l) | 0.74 |
| Fe3+(aq) + e− \(\rightleftharpoons\) Fe2+(aq) | 0.771 |
| Ag+(aq) + e− \(\rightleftharpoons\) Ag(s) | 0.7996 |
| NO3−(aq) + 3H+(aq) + 2e− \(\rightleftharpoons\) HNO2(aq) + H2O(l) | 0.94 |
| Br2(aq) + 2e− \(\rightleftharpoons\) 2Br−(aq) | 1.087 |
| MnO2(s) + 4H+(aq) + 2e− \(\rightleftharpoons\) Mn2+(aq) + 2H2O(l) | 1.23 |
| O2(g) + 4H+(aq) + 4e− \(\rightleftharpoons\) 2H2O(l) | 1.229 |
| Cr2O72−(aq) + 14H+(aq) + 6e− \(\rightleftharpoons\) 2Cr3+(aq) + 7H2O(l) | 1.36 |
| Cl2(g) + 2e− \(\rightleftharpoons\) 2Cl−(aq) | 1.396 |
| \(Ce^{4+}(aq) + e^− \rightleftharpoons Ce^{3+}(aq)\) | 1.61 |
| PbO2(s) + HSO4−(aq) + 3H+(aq) + 2e− \(\rightleftharpoons\) PbSO4(s) + 2H2O(l) | 1.690 |
| H2O2(aq) + 2H+(aq) + 2e− \(\rightleftharpoons\) 2H2O(l) | 1.763 |
| F2(g) + 2e−\(\rightleftharpoons\) 2F−(aq) | 2.87 |
Not all oxidizers and reducers are created equal. The standard reduction potentials in Table \(\PageIndex{1}\) can be interpreted as a ranking of substances according to their oxidizing and reducing power. Strong oxidizing agents are typically compounds with elements in high oxidation states or with high electronegativity, which gain electrons in the redox reaction (Figure \(\PageIndex{1}\)). Examples of strong oxidizers include hydrogen peroxide, permanganate, and osmium tetroxide. Reducing agents are typically electropositive elements such as hydrogen, lithium, sodium, iron, and aluminum, which lose electrons in redox reactions. Hydrides (compounds that contain hydrogen in the formal -1 oxidation state), such as sodium hydride, sodium borohydride and lithium aluminum hydride, are often used as reducing agents in organic and organometallic reactions.
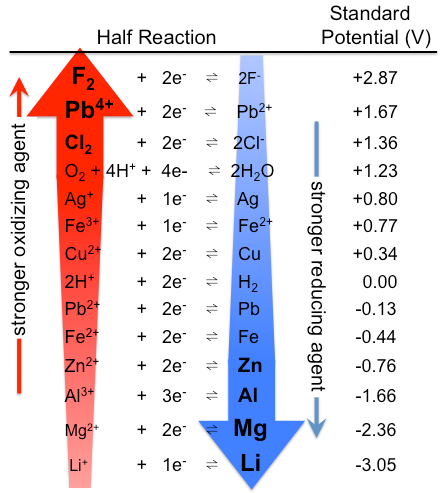
Similarly, all species in Table \(\PageIndex{1}\) that lie above H2 are stronger reductants than H2, and those that lie below H2 are weaker. The strongest reductant in the table is thus metallic lithium, with a standard electrode potential of −3.04 V. This fact might be surprising because cesium, not lithium, is the least electronegative element. The apparent anomaly can be explained by the fact that electrode potentials are measured in aqueous solution, where intermolecular interactions are important, whereas ionization potentials and electron affinities are measured in the gas phase. Due to its small size, the Li+ ion is stabilized in aqueous solution by strong electrostatic interactions with the negative dipole end of water molecules. These interactions result in a significantly greater ΔHhydration for Li+ compared with Cs+. Lithium metal is therefore the strongest reductant (most easily oxidized) of the alkali metals in aqueous solution.
The standard reduction potentials can be interpreted as a ranking of substances according to their oxidizing and reducing power. Species in Table \(\PageIndex{1}\) that lie above H2 are stronger reducing agents (more easily oxidized) than H2. Species that lie below \(\ce{H2}\) are stronger oxidizing agents.
Because the half-reactions shown in Table \(\PageIndex{1}\) are arranged in order of their E° values, we can use the table to quickly predict the relative strengths of various oxidants and reductants. Any species on the left side of a half-reaction will spontaneously oxidize any species on the right side of another half-reaction that lies below it in the table. Conversely, any species on the right side of a half-reaction will spontaneously reduce any species on the left side of another half-reaction that lies above it in the table. We can use these generalizations to predict the spontaneity of a wide variety of redox reactions (E°cell > 0), as illustrated in Example \(\PageIndex{1}\).
The black tarnish that forms on silver objects is primarily \(\ce{Ag2S}\). The half-reaction for reversing the tarnishing process is as follows:
\[\ce{Ag2S(s) + 2e^{−} → 2Ag(s) + S^{2−} (aq)} \quad E°=−0.69\, V \nonumber \]
- Referring to Table \(\PageIndex{1}\), predict which species—H2O2(aq), Zn(s), I−(aq), Sn2+(aq)—can reduce Ag2S to Ag under standard conditions.
- Of these species—H2O2(aq), Zn(s), I−(aq), Sn2+(aq), identify which is the strongest reducing agent in aqueous solution and thus the best candidate for a commercial product.
- From the data in Table \(\PageIndex{1}\), suggest an alternative reducing agent that is readily available, inexpensive, and possibly more effective at removing tarnish.

Given: reduction half-reaction, standard electrode potential, and list of possible reductants
Asked for: reductants for \(\ce{Ag2S}\), strongest reductant, and potential reducing agent for removing tarnish
Strategy:
A From their positions in Table \(\PageIndex{1}\), decide which species can reduce \(\ce{Ag2S}\). Determine which species is the strongest reductant.
B Use Table \(\PageIndex{1}\) to identify a reductant for \(\ce{Ag2S}\) that is a common household product.
Solution
We can solve the problem in one of two ways: (1) compare the relative positions of the four possible reductants with that of the Ag2S/Ag couple in Table \(\PageIndex{1}\) or (2) compare E° for each species with E° for the Ag2S/Ag couple (−0.69 V).
- A The species in Table \(\PageIndex{1}\) are arranged from top to bottom in order of increasing reducing strength. Of the four species given in the problem, I−(aq), Sn2+(aq), and H2O2(aq) lie above Ag2S, and one [Zn(s)] lies below it. We can therefore conclude that Zn(s) can reduce Ag2S(s) under standard conditions, whereas I−(aq), Sn2+(aq), and H2O2(aq) cannot. Sn2+(aq) and H2O2(aq) appear twice in the table: on the left side (oxidant) in one half-reaction and on the right side (reductant) in another.
- The strongest reductant is Zn(s), the species on the right side of the half-reaction that lies closer to the bottom of Table \(\PageIndex{1}\) than the half-reactions involving I−(aq), Sn2+(aq), and H2O2(aq). (Commercial products that use a piece of zinc are often marketed as a “miracle product” for removing tarnish from silver. All that is required is to add warm water and salt for electrical conductivity.)
- B Of the reductants that lie below Zn(s) in Table \(\PageIndex{1}\), and therefore are stronger reductants, only one is commonly available in household products: Al(s), which is sold as aluminum foil for wrapping foods.
Use the data in Table \(\PageIndex{1}\) to determine whether each reaction is likely to occur spontaneously under standard conditions:
- \(\ce{Sn(s) + Be^{2+}(aq) → Sn^{2+}(aq) + Be(s)}\)
- \(\ce{MnO2(s) + H2O2(aq) + 2H^{+}(aq) → O2(g) + Mn^{2+}(aq) + 2H2O(l)}\)
Given: redox reaction and list of standard electrode potentials (Table \(\PageIndex{1}\))
Asked for: reaction spontaneity
Strategy:
- Identify the half-reactions in each equation. Using Table \(\PageIndex{1}\), determine the standard potentials for the half-reactions in the appropriate direction.
- Use the \(E_{cell}=E^o_{srp}(cathode) - E^o_{srp}(anode)\) equation to calculate the standard cell potential for the overall reaction. From this value, determine whether the overall reaction is spontaneous.
Solution
- A Metallic tin is oxidized to \(\ce{Sn^{2+}(aq)}\), and \(\ce{Be^{2+}(aq)}\) is reduced to elemental beryllium. We can find the standard electrode potentials for the latter (reduction) half-reaction (−1.99 V) and for the former (oxidation) half-reaction (−0.14 V) directly from Table \(\PageIndex{1}\).
B Adding the two half-reactions gives the overall reaction: \[\begin{align*}\textrm{cathode} &: \ce{Be^{2+}(aq)} +\ce{2e^-} \rightarrow \ce{Be(s)} \\ \textrm{anode} &: \ce{Sn(s)} \rightarrow \ce{Sn^{2+}(s)} +\ce{2e^-} \\ \hline \textrm{overall} &: \ce{Sn(s)} + \ce{Be^{2+}(aq)} \rightarrow \ce{Sn^{2+}(aq)} + \ce{Be(s)} \end{align*} \] with \[\begin{align*} E^\circ_{\textrm{cathode}} &=\textrm{-1.99 V} \\[4pt] E^\circ_{\textrm{anode}} &=\textrm{-0.14 V} \\[4pt] E^\circ_{\textrm{cell}} &=E^\circ_{\textrm{cathode}}-E^\circ_{\textrm{anode}} \\[4pt] &=-\textrm{1.85 V} \end{align*} \]
The standard cell potential is quite negative, so the reaction will not occur spontaneously as written. That is, metallic tin cannot reduce Be2+ to beryllium metal under standard conditions. Instead, the reverse process, the reduction of stannous ions (Sn2+) by metallic beryllium, which has a positive value of E°cell, will occur spontaneously.
- A \(\ce{MnO2}\) is the oxidant (\(\ce{Mn^{4+}}\) is reduced to \(\ce{Mn^{2+}}\)), while \(\ce{H2O2}\) is the reductant (\(\ce{O^{2−}}\) is oxidized to \(\ce{O2}\)). We can obtain the standard electrode potentials for the reduction and oxidation half-reactions directly from Table \(\PageIndex{1}\).
B The two half-reactions and their corresponding potentials are as follows: \[\begin{align*}\textrm{cathode} &: \ce{MnO_2(s)}+\ce{4H^+(aq)}+\ce{2e^-} \rightarrow\ce{Mn^{2+}(aq)}+\ce{2H_2O(l)} \\ \ce{anode} &: \ce{H_2O_2(aq)}\rightarrow\ce{O_2(g)}+\ce{2H^+(aq)}+\ce{2e^-} \\\hline \textrm{overall} &: \ce{MnO_2(s)}+\ce{H_2O_2(aq)}+\ce{2H^+(aq)}\rightarrow\ce{O_2(g)}+\ce{Mn^{2+}(aq)}+\ce{2H_2O(l)} \end{align*} \] with \[\begin{align*} E^\circ_{\textrm{cathode}} &=\textrm{1.23 V} \\[4pt] E^\circ_{\textrm{anode}} &=\textrm{0.70 V} \\[4pt] E^\circ_{\textrm{cell}} &=E^\circ_{\textrm{cathode}}-E^\circ_{\textrm{anode}} \\[4pt] &=+\textrm{0.52 V} \end{align*} \]
The standard potential for the reaction is positive, indicating that under standard conditions, it will occur spontaneously as written. Hydrogen peroxide will reduce \(\ce{MnO2}\), and oxygen gas will evolve from the solution.
Use the data in Table \(\PageIndex{1}\) to determine whether each reaction is likely to occur spontaneously under standard conditions:
- \(\ce{2Ce^{4+}(aq) + 2Cl^{−}(aq) → 2Ce^{3+}(aq) + Cl2(g)}\)
- \(\ce{4MnO2(s) + 3O2(g) + 4OH^{−}(aq) → 4MnO4^{−}(aq) + 2H2O}\)
- Answer a
-
spontaneous with \(E^o_{cell} = 1.61\, V - 1.396\, V = 0.214\, V\)
- Answer b
-
nonspontaneous with \(E^°_{cell} = −0.20\, V\)
Although the sign of \(E^o_{cell}\) tells us whether a particular redox reaction will occur spontaneously under standard conditions, it does not tell us to what extent the reaction proceeds, and it does not tell us what will happen under nonstandard conditions. To answer these questions requires a more quantitative understanding of the relationship between electrochemical cell potential and chemical thermodynamics.
Summary
The relative strengths of various oxidants and reductants can be predicted using \(E^o\) values. The oxidative and reductive strengths of a variety of substances can be compared using standard electrode potentials. Apparent anomalies can be explained by the fact that electrode potentials are measured in aqueous solution, which allows for strong intermolecular electrostatic interactions, and not in the gas phase.
Conceptual Problems
- The order of electrode potentials cannot always be predicted by ionization potentials and electron affinities. Why? Do you expect sodium metal to have a higher or a lower electrode potential than predicted from its ionization potential? What is its approximate electrode potential?
- Without referring to tabulated data, of Br2/Br−, Ca2+/Ca, O2/OH−, and Al3+/Al, which would you expect to have the least negative electrode potential and which the most negative? Why?
- Because of the sulfur-containing amino acids present in egg whites, eating eggs with a silver fork will tarnish the fork. As a chemist, you have all kinds of interesting cleaning products in your cabinet, including a 1 M solution of oxalic acid (H2C2O4). Would you choose this solution to clean the fork that you have tarnished from eating scrambled eggs?
- The electrode potential for the reaction Cu2+(aq) + 2e− → Cu(s) is 0.34 V under standard conditions. Is the potential for the oxidation of 0.5 mol of Cu equal to −0.34/2 V? Explain your answer.
- Refer to Table \(\PageIndex{1}\) to predict
- Which species—Sn4+(aq), Cl−(aq), Ag+(aq), Cr3+(aq), and/or H2O2(aq)—can oxidize MnO2(s) to MNO4− under standard conditions.
- Which species—Sn4+(aq), Cl−(aq), Ag+(aq), Cr3+(aq), and/or H2O2(aq)—is the strongest oxidizing agent in aqueous solution.
Conceptual Answer
- No; E° = −0.691 V for Ag2S(s) + 2e− → Ag(s) + S2−(aq), which is too negative for Ag2S to be spontaneously reduced by oxalic acid [E° = 0.49 V for 2CO2(g) + 2H+(aq) + 2e− → H2C2O4(aq)]
5.
- Ag+(aq); H2O2(aq)
- H2O2(aq)

