6.3.1: Brønsted-Lowry Concept
- Page ID
- 151389
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Brønsted-Lowry acid-base concept
The Brønsted-Lowry acid-base concept overcomes the Arrhenius system's inability to describe reactions that take place outside of aqueous solution by moving the focus away from the solution and onto the acid and base themselves. It does this by redefining acid-base reactivity as involving the transfer of a hydrogen ion, \(H^+\), between an acid and a base. Specifically, a Brønsted acid is a substance that loses an \(H^+\) ion by donating it to a base. This means that a Brønsted base is defined as a substance which accepts \(H^+\) from an acid when it reacts.
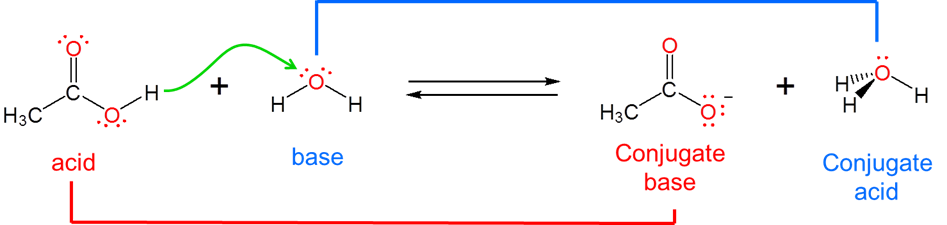
Because the Brønsted-Lowry concept is concerned with \(H^+\) ion transfer rather than the creation of a particular chemical species, it is able to handle a diverse array of acid-base concepts. In fact, from the viewpoint of the Brønsted-Lowry concept, Arrhenius acids and bases are just a special case involving hydrogen ion donation and acceptance involving water. Arrhenius acids donate \(H^+\) ion to water, which acts as a Brønsted base in accepting it to give \(H_3O^+\):
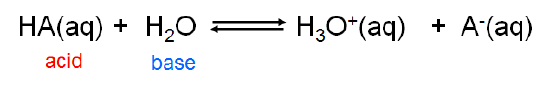 \[\label{ 6.3.1} \]
\[\label{ 6.3.1} \]
Similarly, Arrhenius bases act as Brønsted bases in accepting a hydrogen ion from the Brønsted acid water:
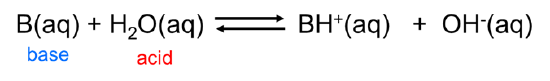 \[ \nonumber \]
\[ \nonumber \]
In this way it can be seen that Arrhenius acids and bases are defined in terms of their causing hydrogen ions to be donated to and abstracted from water, respectively, while Brønsted acids and bases are defined in terms of their ability to donate and accept hydrogen ions to and from anything.
Becasue the Brønsted-Lowry concept can handle any sort of hydrogen ion transfer it readily accommodates many reactions that Arrhenius theory cannot, including those that take place outside of water, such as the reaction between gaseous hydrochloric acid and ammonia:
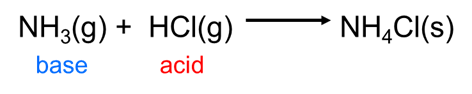 \[ \nonumber \]
\[ \nonumber \]
The classification of acids as strong or weak usually refers to their ability to donate or abstract hydrogen ions to or from water to give \(H_3O^+\) and \(OH^-\), respectively, i.e., their Arrhenius acidity and basicity. However, acids and bases may be classified as strong and weak under the Brønsted-Lowry definition based on whether they completely transfer or accept hydrogen ions; it is just that in this case it is important to specify the conditions under which a given acid or base acts strong or weak. For example, acetic acid acts as a weak acid in water but is a strong acid in triethylamine, since in the latter case it completely transfers a hydrogen ion to triethylamine to give triethylammonium acetate. Alternatively, the acidity or basicity of a compound may be specified using a thermodynamic scale like the Hammett acidity.
Conjugate Acids and Bases
By redefining acids and bases in terms of hydrogen ion donation and acceptance, the Brønsted-Lowry system makes it easy to recognize that when an acid loses its hydrogen ion it becomes a substance that is capable of receiving it back again, namely, a base. Consider, for example, the base dissociation of ammonia in water. When ammonia acts as a Brønsted base and receives a hydrogen ion from water, ammonium ion and hydroxide are formed:
 \[ \nonumber \]
\[ \nonumber \]
The ammonium ion is itself a weak acid that can undergo dissociation:
 \[ \nonumber \]
\[ \nonumber \]
In this case ammonia and ammonium ion are acid-base conjugates. In general acids and bases that differ by a single ionizable hydrogen ion are said to be conjugates of one another.
The strengths of conjugates vary reciprocally with one another, so the stronger the acid the weaker the base and vice versa. For example, in water, acetic acid acts as a weak Brønsted acid:
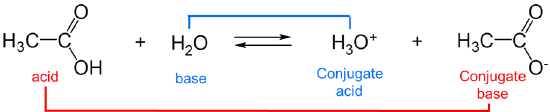 \[ \nonumber \]
\[ \nonumber \]
and acetic acid's conjugate base, acetate, acts as a weak Brønsted base.
 \[ \nonumber \]
\[ \nonumber \]
However, in liquid ammonia acetic acid acts as a strong Brønsted acid:
 \[ \nonumber \]
\[ \nonumber \]
while its conjugate base, acetate, is neutral.
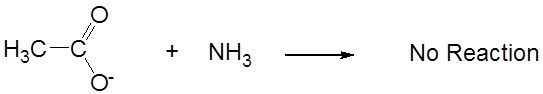 \[ \nonumber \]
\[ \nonumber \]
The reciprocal relationship between the strengths of acids and their conjugate bases has several consequences:
- Under conditions when an acid or base acts as a weak acid or base its conjugate acts as weak as well. Conversely, when an acid or base acts as a strong acid or base its conjugate acts as a neutral species.
- When a Brønsted acid and base react with one another, the equilibrium favors formation of the weakest acid-base pair. That is why the acid-base reaction between acetic acid and ammonia in liquid ammonia proceeded to give the weak acid ammonium ion and neutral acetate. This consequence is particularly important for understanding the behavior of acids and bases in nonaqueous solvents, as illustrated by the following example.
Can a solution of lithium diisopropylamide in heptane be used to form lithium cyclopentadienide? The \(pK_a\) of cyclopentadiene and diisopropylamine are ~15 and 40, respectively, and the proposed reaction is as follows:
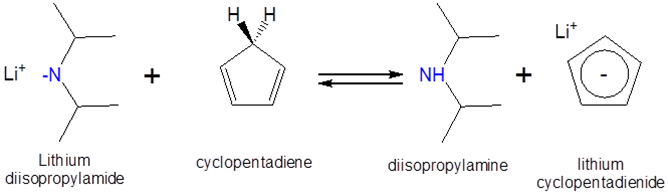
- Solution:
-
Since cyclopentadiene is a stronger acid than diisopropylamine (the stronger the acid the lower the \(pK_a\)) the equilibrium will favor protonation of the diisopropylamine by cyclopentadiene. Consequently addition of a heptane solution of lithium diisopropylamide to monomeric cyclopentadiene should give lithium cyclopentadienide.

