5.P: Problems
- Page ID
- 151384
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Concept Review Questions
1. What are the assumptions (axioms) of molecular orbital (MO) theory?
2. Explain qualitatively why the vectorial addition of atomic orbitals creates molecular orbitals (which underlying physical phenomenon is described by the vectorial addition?).
3. Explain qualitatively why molecular orbital theory is suitable to describe covalent bonding.
4. What are the three criteria that determine the degree of covalent interaction in MO theory?
5. Which three rules determine the degree of orbital overlap in MO theory?
6. Explain why the combination of a large, diffuse orbital and a small orbital produces only weak covalent interaction.
7. Explain why sigma interactions between atomic orbitals typically produce larger orbital overlaps than pi interactions.
8. Explain why the combination of orbitals of the same energy leads to the largest degree of covalent interaction.
9. What can be said about energy and location of a bonding and an anti-bonding molecular orbital that are made from atomic orbitals of large energy difference?
10. MO theory – even though designed for covalent bonding – can also make statements about ionic bonding. Explain why.
11. Explain the principles of SALC.
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.
Homework Problems
Section 1
Exercise 1
What will most likely lead to the smallest covalent interaction?
a) Overlap of a small and a large orbital.
b) Overlap of two small orbitals.
c) Overlap of two large orbitals.
- Answer
-
a) Overlap of a small and a large orbital.
Exercise 2
What will most likely lead to the largest covalent interaction?
a) orbital overlap in sigma-fashion
b) orbital overlap in pi-fashion
c) orbital overlap in delta-fashion
- Answer
-
a) orbital overlap in sigma-fashion
Exercise 3
Qualitatively construct the MO diagrams composed of
a) two 2s atom orbitals A and B of equal energy.
b) two 2s atom orbitals where the orbital energy of atom A is significantly higher than that of B. If both the bonding and the antibonding MO are filled with electrons, where will bonding and antibonding electrons primarily be located? Briefly explain your decision.
- Answer
-

Exercise 4
Decide by “inspection” which of the following combinations of orbitals have the “right” symmetries to form molecular orbitals.
a) The 2px orbital of the first N atom and the 2py orbital of the second N atom in the molecule N2. The z axis is defined as the bond axis in N2.
b) The F 2px and the H 1s orbital in the HF molecule. The z axis is defined as the bond axis.
c) The 2pz orbital of F and the 1s orbital in the HF molecule. The z axis is defined as the bond axis.
- Answer
-
a)
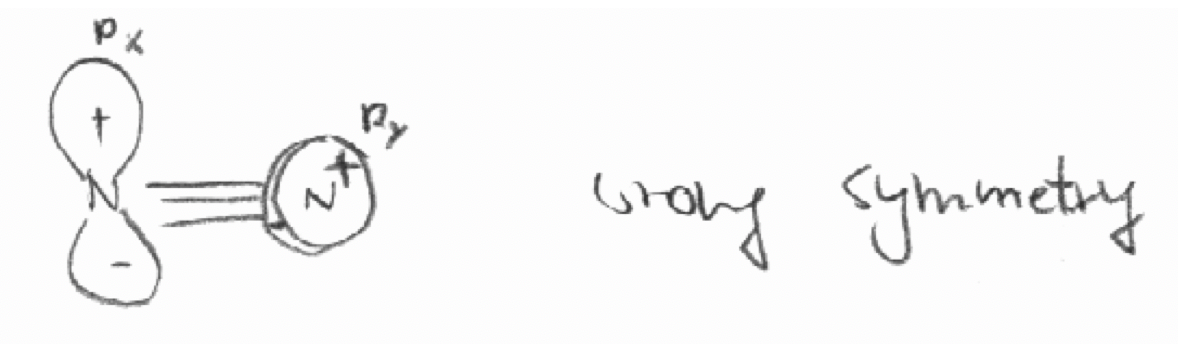
b)

c)
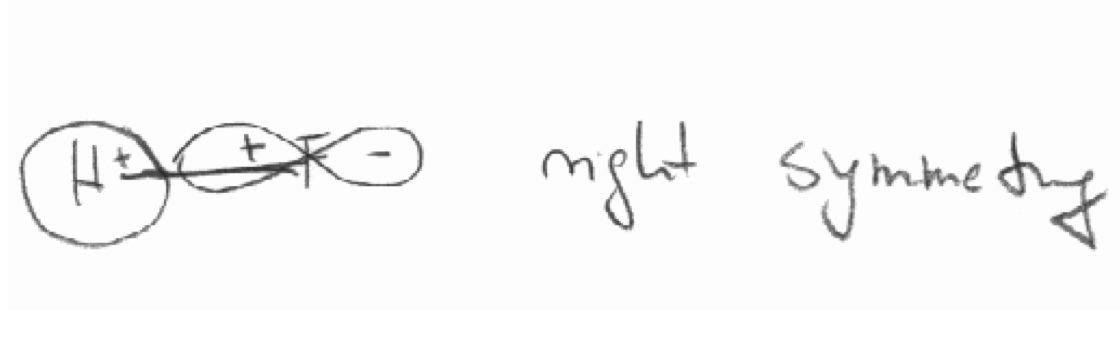
Exercise 5
The CH4 molecule belongs to the point group Td. You can find the character table of the point group in the internet.
a) Calculate the reducible representation for the ligand group orbitals (LGOs).
b) Calculate the irreducible representations of the ligand group orbitals (LGOs).
c) Draw a qualitative molecular orbital diagram for CH4.
- Answer
-
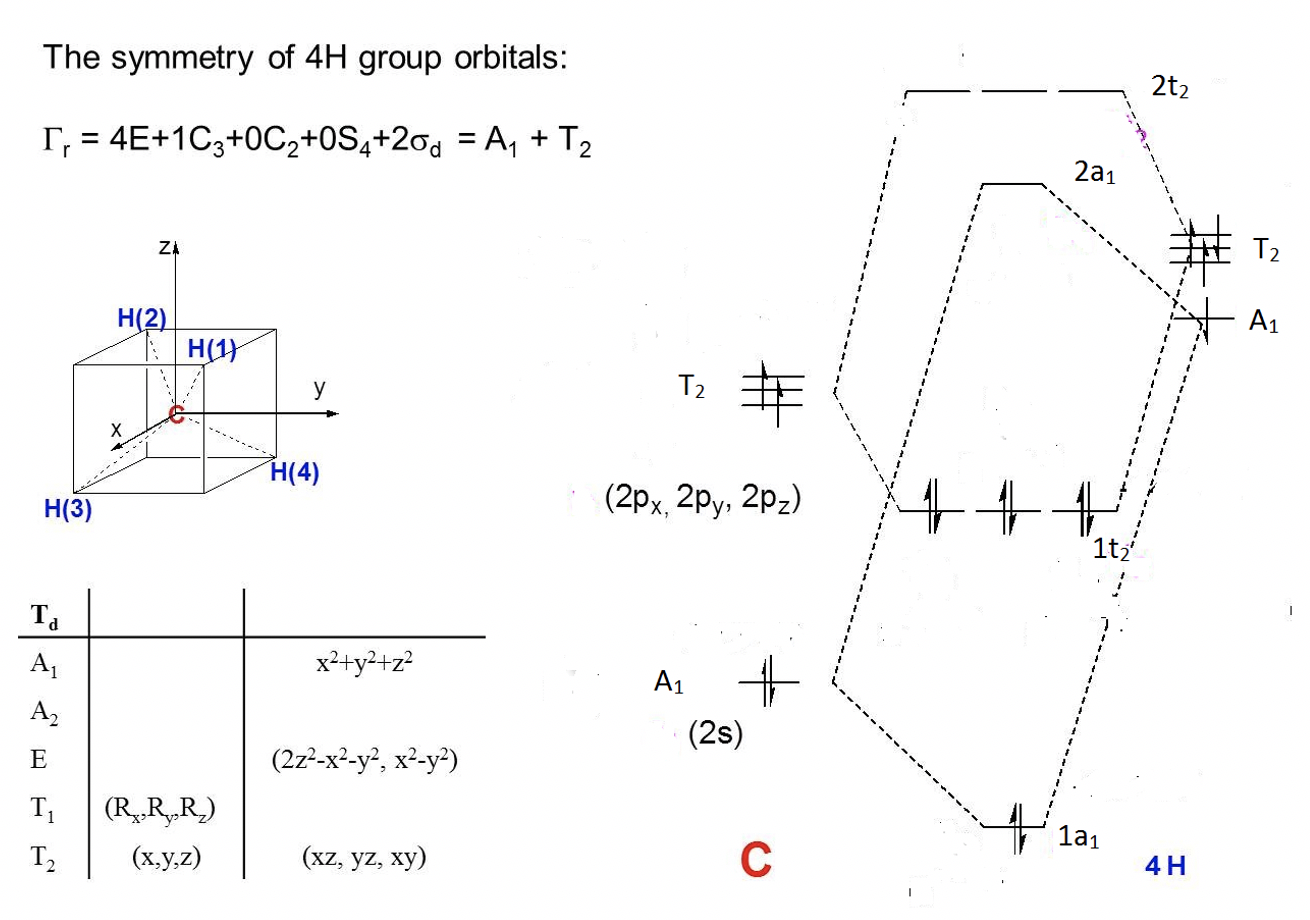
Exercise 6
Which are the symmetry types of the central atom orbitals in the PCl5 molecule?
- Answer
- 1. Determine point group of PCl5. --> D3h.
- 2. Decide what are the valence orbitals of the central atom: 3s, 3p
- 3. Look up the character table of D3h, e.g., in the internet. You will find their symmetries to be: A1' (3s), A2'' (3pz), E'(3px, 3py)
Exercise 7
For the hypothetical BrKr+ molecule: Toward which atom is the HOMO polarized? Explain briefly why.
- Answer
-
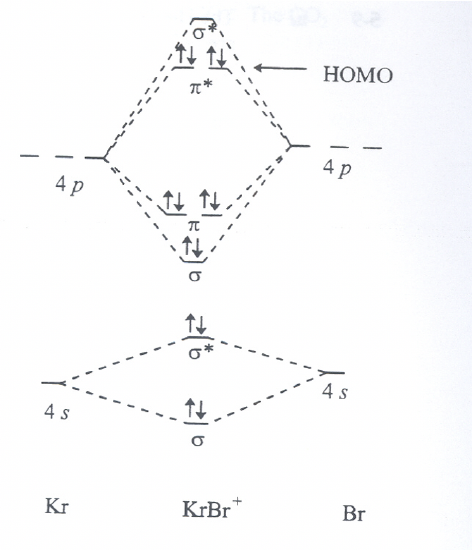

Exercise 8
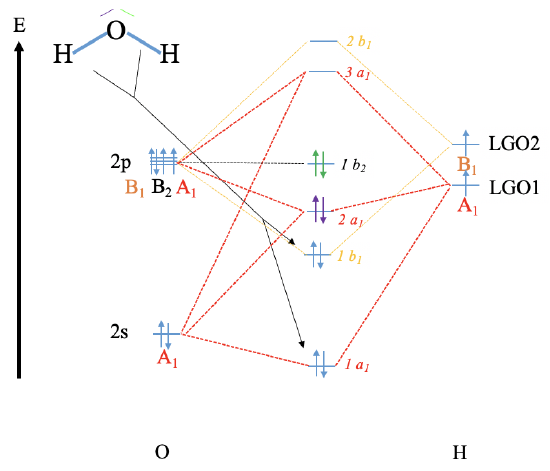
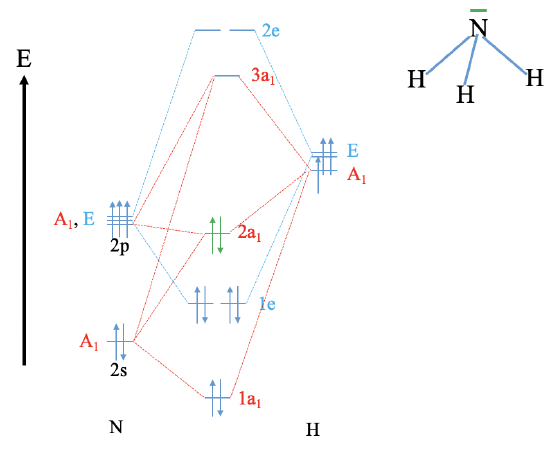
Reconstruct the MO diagram for water and NH3 (repeat what we did in class without looking at your notes (only use the respective character tables).
- Answer
-
Water
NH3
Dr. Kai Landskron (Lehigh University). If you like this textbook, please consider to make a donation to support the author's research at Lehigh University: Click Here to Donate.
A Molecular Orbital Diagram for a diatomic molecule (two atoms) always has the same basic pattern.
- Draw a picture of the levels.
- Label each level with σ, σ*, π, π*
- Answer
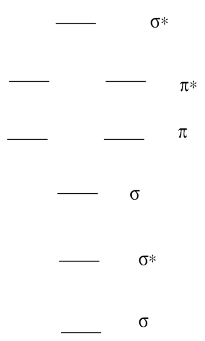
A Molecular Orbital Diagram for a diatomic molecule (two atoms) varies in the number of electrons. How do you populate the electrons?
- Answer
-
• Count the valence electrons on the molecule. That's the number of valence electrons on each atom, adjusted for any charge on the molecule. (eg C22- has 10 valence electrons: 4 from each carbon -- that's 8 -- and two more for the 2- charge).
• Fill electrons into the lowest energy orbitals first.
• Pair electrons after all orbitals at the same energy level have one electron.
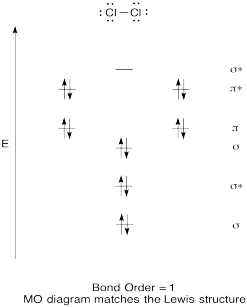
Construct a qualitative molecular orbital diagram for chlorine, Cl2. Compare the bond order to that seen in the Lewis structure (remember that an electron in an antibonding orbital cancels the stabilization due to bonding of an electron in a bonding orbital).
- Answer
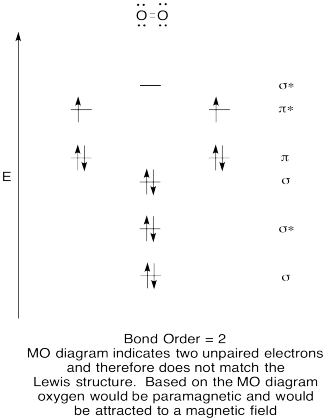
- Construct a qualitative molecular orbital diagram for oxygen, O2.
- Compare the bond order to that seen in the Lewis structure.
- How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- Compounds that have all of their electrons paired are referred to as diamagnetic. Those with unpaired electrons are referred to as paramagnetic. Paramagnetic materials are attracted by a magnetic field, but diamagnetic things are not. How would you expect molecular oxygen to behave?
- Answer
-
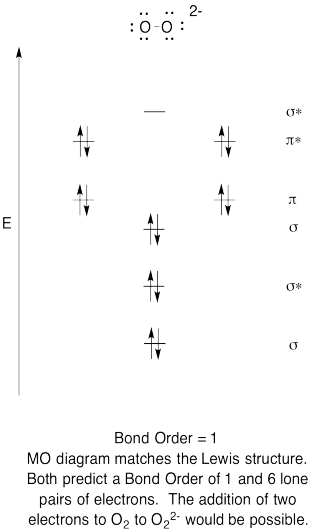
- Construct a qualitative molecular orbital diagram for peroxide anion, O22-.
- Compare the bond order to that seen in the Lewis structure.
- How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- Based on molecular orbital pictures, how easily do you think dioxygen could be reduced to peroxide (through the addition of two electrons)?
- Answer
-
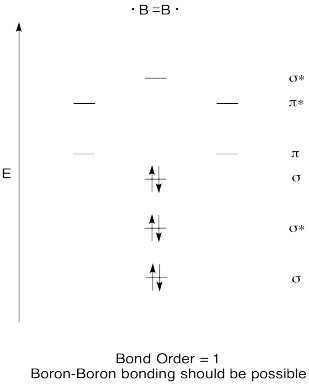
Construct a qualitative molecular orbital diagram for diboron, B2. Do you think boron-boron bonds could form easily, based on this picture?
- Answer
-
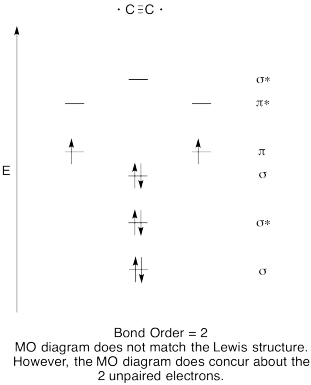
- Construct a qualitative molecular orbital diagram for dicarbon, C2.
- Compare the bond order to that seen in the Lewis structure.
- How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- Answer
-
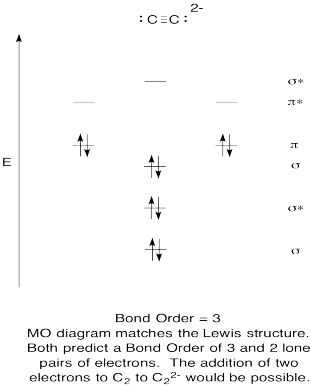
- Construct a qualitative molecular orbital diagram for acetylide anion, C22-.
- Compare the bond order to that seen in the Lewis structure.
- How else does this MO picture of oxygen compare to the Lewis structure? What do the two structures tell you about electron pairing?
- Based on molecular orbital pictures, how easily do you think dicarbon could be reduced to acetylide (through the addition of two electrons)?
- Answer
-
Make drawings and notes to summarize the effect of populating antibonding orbitals.
- Answer
-

Researchers at Johns Hopkins recently reported the formation of Na4Al2 in a pulsed arc discharge (they put a lot of electric current through a sample of sodium and aluminum; Xinxing Zhang, Ivan A. Popov, Katie A. Lundell, Haopeng Wang, Chaonan Mu, Wei Wang, Hansgeorg Schnöckel, Alexander I. Boldyrev, Kit H. Bowen, Angewandte Chemie International Edition, 2018, 57(43), 14060-14064. Copyright 2018, John Wiley & Sons. Used with permission.).
- The compound is ionic. Explain which atoms form the cations, based on periodic trends.
- Therefore, what atoms form the anion?
- The anion is one molecule. What is the charge on this molecule?
- Show how to calculate the total valence electrons in this molecular anion.
- Draw a Lewis structure for this molecular anion.
- Construct a diatomic molecular orbital energy level diagram for this molecule. Label the energy levels (sigma, pi, etc.) and add in the correct number of electrons.
- Show how to calculate the bond order in the molecule.
- Answer
-
a) Na, because Na has a lower ionization potential (and a lower electronegativity) than Al.
b) Al
c) 4-, because there are four Na+
d) total e- = 2 x 3 e- (per Al) + 4 e- (for the negative charge) = 10 e-

g) \(\textrm{bond order} = \frac{( \# bonding \: e^{-} - \# antibonding \: 3^{-})}{2} = \frac{8-2}{2}= 3\)
Draw the molecular orbital diagram for (\(\ce{NO^-}\)).
- Answer
-
Add texts here. Do not delete this text first.
Draw and compare the molecular orbital diagrams to the Lewis structure diagrams for \(\ce{O2}\), \(\ce{O2^-}\), and \(\ce{O2^2-}\).
- Answer
-
The Lewis structures and MO diagrams are shown below. In general, the bond order derived from the MO diagram agrees with the Lewis structure for each species. In the case of the two ions, the number of unpaired electrons from MO theory and the Lewis structure also agrees. In the case of dioxygen, however, there is an inconsistency between the Lewis representation and the MO diagram. While the Lewis structure would lead us to believe that all electrons are paired, the MO diagram indicates paramagnetism, with two unpaired electrons. The MO diagram explains the magnetic behaviour of dioxygen.

Draw the molecular orbital diagram for hydroxide ion (\(\ce{OH^-}\)).
- Answer
-
Add texts here. Do not delete this text first.
Draw the molecular orbital diagram for hydroxide fluoride (\(\ce{HF}\)).
- Answer
-
Add texts here. Do not delete this text first.
Draw the molecular orbital diagram for borane (\(\ce{BN}\)).
- Answer
-
Add texts here. Do not delete this text first.
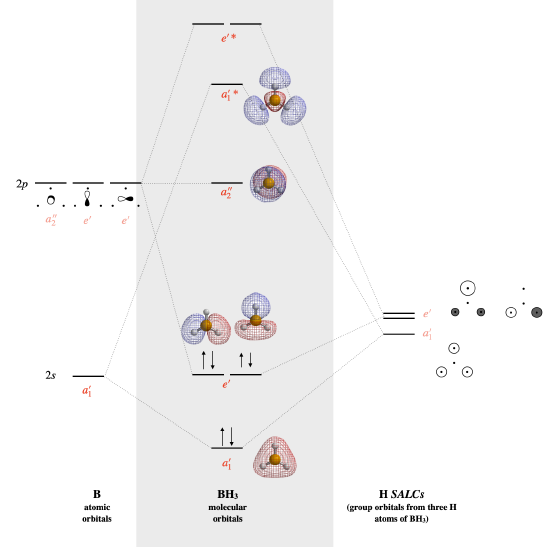
BH3
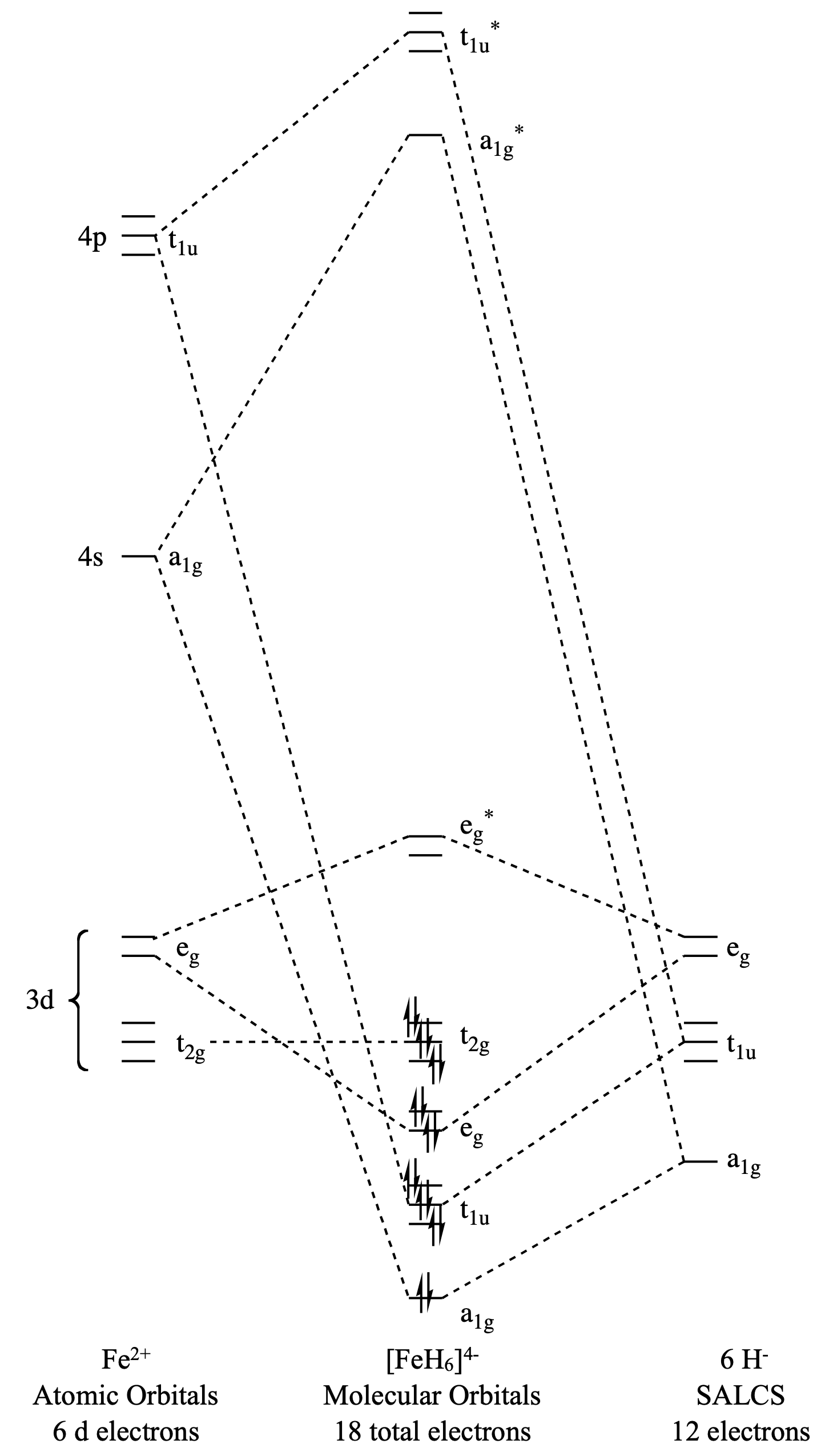
Draw the molecular orbital diagram for (\(\ce{FeH6}\)).
- Answer
-
Draw the molecular orbital diagram for boron trifluoride (\(\ce{BF3}\)).
- What is the non-bonding orbital?
- What are the HOMO and LUMO orbitals?
- Why does e' have 2 lines of energy levels compared to a1', which has only a 1-line energy level?
- What is the bond order of \(\ce{BH3}\) in this MO diagram?
- Answer
-
The calculated MO diagram is shown below.
- \(a_2''\) is the lone non-bonding orbital.
- The HOMO is the \(a_2''\) nonbonding orbital, the LUMO is a bonding \(e'\) set of two degenerate orbitals/
- \(e'\) is doubly degenerate
- The bond order is 3