5.3.3: Ionic Compounds and Molecular Orbitals
- Page ID
- 243624
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ionic interactions lie at one extreme on a spectrum of bonding. On the opposite end of the spectrum are the non-polar covalent bonds (e.g., homonuclear diatomics). In these molecules, molecular orbitals are formed by equal-energy atomic orbitals, resulting in electron density evenly distributed over the molecule. In the middle of the spectrum are the cases of polar covalent bonds (e.g., heteronuclear diatomics), in which atomic orbitals of unequal energies contribute unequally to molecular orbitals, resulting in uneven distribution of electron density across the molecule. In the case of polar bonds, the electron density is shifted toward the more electronegative atom since that atom contributes more to the lowest energy bonding molecular orbitals. Molecular orbital diagrams can be drawn for ionic compounds as if they are extremely polar bonds in which electrons are not only shifted toward, but are transferred completely to the more electronegative atom.
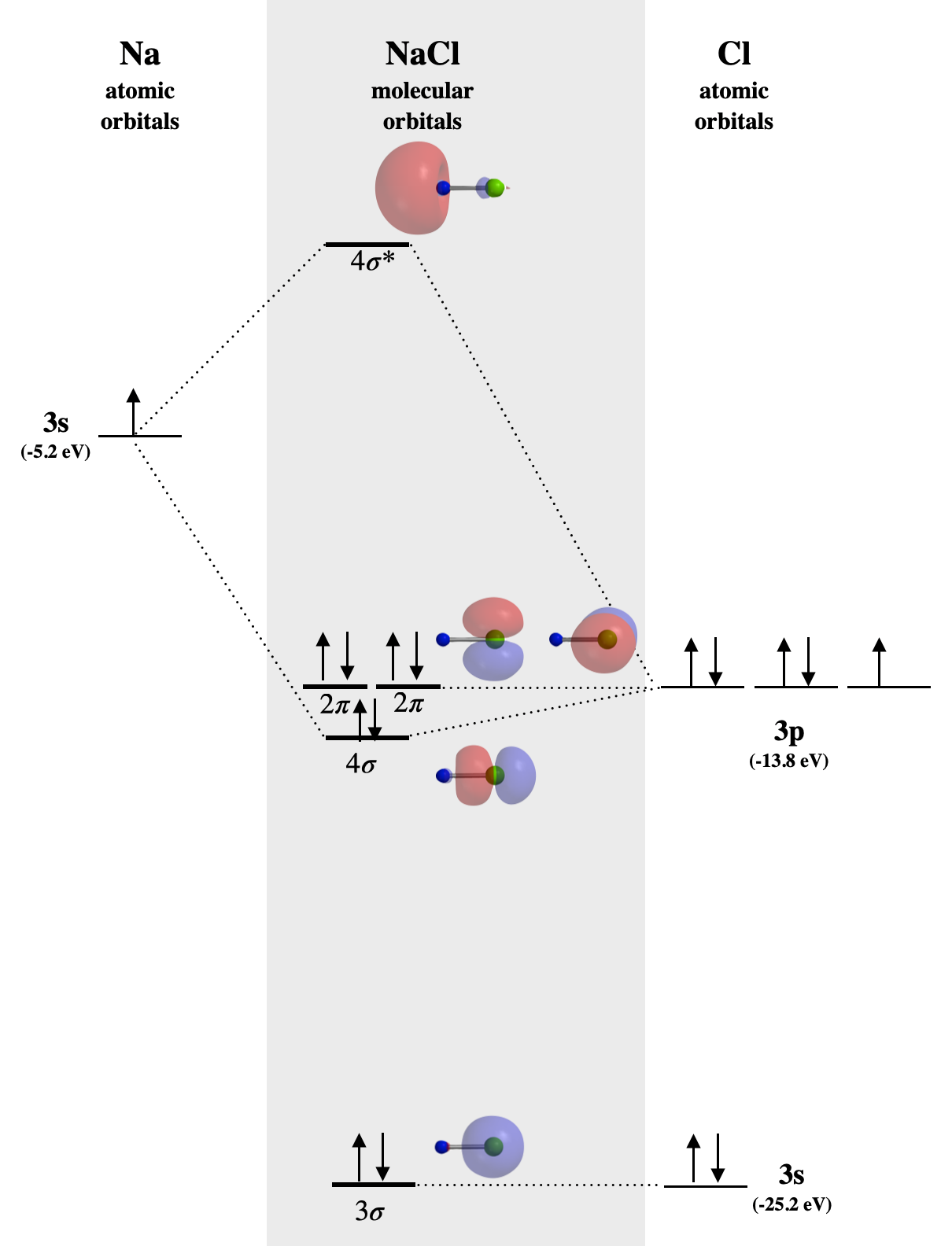
Example: NaCl
In \(\ce{NaCl}\), the sodium \(3s\) orbital (-5.2 eV) is significantly higher in energy than the chlorine valence orbitals. The chlorine \(3s\) and \(3p_z\) orbitals have compatible symmetry, yet only the \(3p_z\) orbital (-13.8 eV) is close enough in energy to interact with the Na \(3s\); still, the energy difference is large enough to make bonding weak. The Na \(3s\) orbital combines with Cl \(3p_z\) to form the molecular orbitals labeled \(4\sigma\) and \(4\sigma^*\) in Figure \(\PageIndex{1}\). The \(4\sigma\) orbital is weakly bonding, but is very close in energy to the Cl \(3p_z\) orbital, and is mostly Cl-like in character. Notice that all \(\sigma\) orbitals look very much like either \(s\) or \(p\) orbitals centered on the \(\ce{Cl}\) atom, while the \(4\sigma^*\) orbital is centered almost entirely on Na. The lack of molecular orbitals that are distributed over both atoms at once is consistent with a lack of significant covalent bond character in \(\ce{NaCl}\). The bonding here is characterized by transfer of one electron from \(\ce{Na}\) to \(\ce{Cl}\) and is almost entirely electrostatic. Bonding that is mostly electrostatic in character is non-directional, unlike true covalent bonding.
Draw the molecular orbital diagram for \(\ce{LiF}\). Make sure to label all molecular orbitals appropriately, and specify whether they are mostly bonding, non-bonding, or antibonding. Identify the HOMO and LUMO. Sketch the approximate shapes of all orbitals.
- Answer
-
We expect \(\ce{LiF}\) to be an ionic compound because the energy difference in valence orbitals is at least 10-14 eV. (See Table 5.3.1) There are a variety of ways used to label molecular orbitals. In the figure below, we are using the convention of labeling each type of orbital with numbers starting from the lowest-energy orbitals. The \(1\sigma\) orbital would be mostly F \(1s\) in character and is not shown. The \(2\sigma\) orbital is mostly non-bonding in nature, although it has a very small contribution from \(2s\) of Li due to compatible symmetry. The \(3\sigma\) orbital is slightly bonding but it is mostly F\(2p\) in character. The two \(1\pi\) orbitals are completely non-bonding. The \(3\sigma^*\) orbital is antibonding.
- HOMO is \(1\pi\)
- LUMO is \(3\sigma^*\)
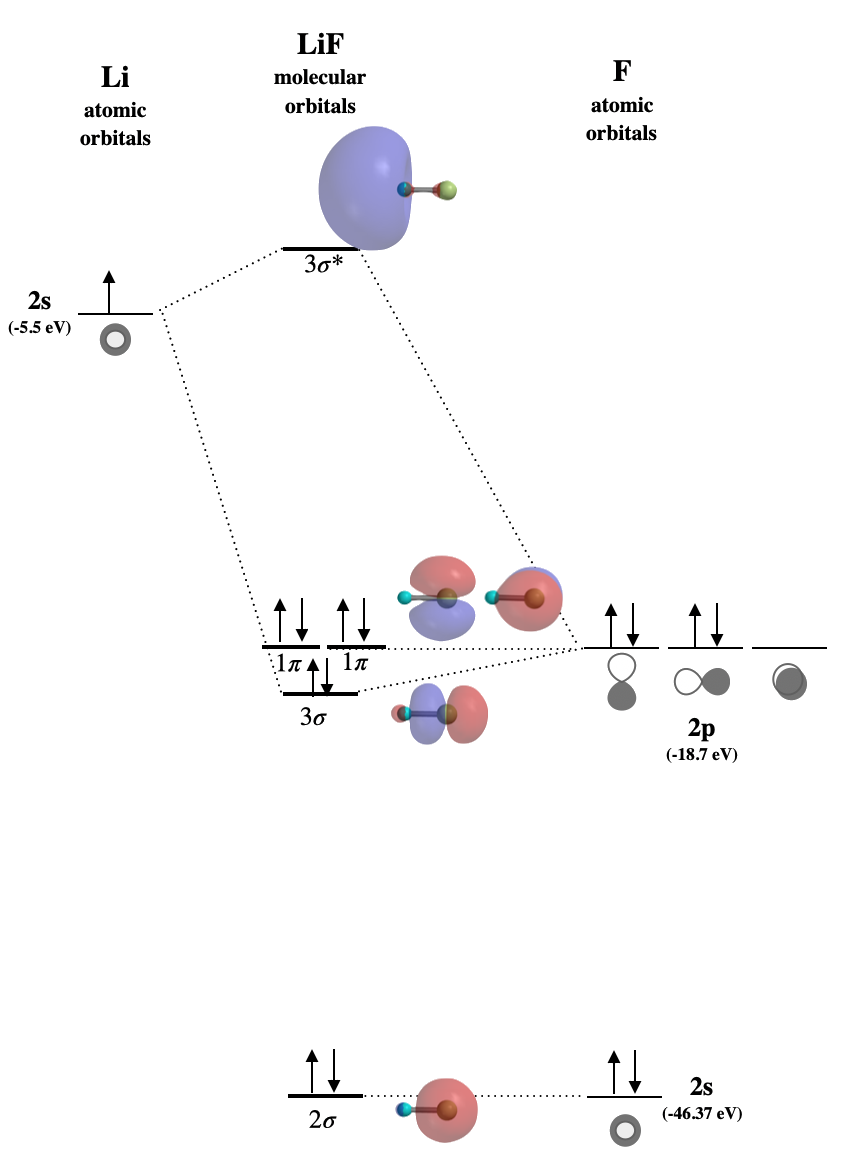
Figure for Exercise \(\PageIndex{1}\): Molecular orbital diagram for the ionic compund, LiF. (CC-BY-NC-SA, Kathryn Haas)


