3.1.4: Lewis Fails to Predict Unusual Cases - Boron and Beryllium
- Page ID
- 167331
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two notable cases where Lewis theory fails to predict structure are the cases of beryllium (\(\ce{Be}\)) and boron (\(\ce{B}\)). These two atoms are in period 2 (\(n=2\)) of the periodic table and their atoms have the valence electron configurations of \(2s^2\) and \(2s^22p^1\), respectively.
Beryllium
The Lewis electron dot structures are shown below for \(\ce{BeX2}\), where \(\ce{X}\) is one of the halogens, \(\ce{F}\) or \(\ce{Cl}\).
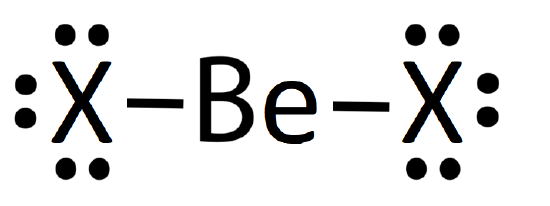
Each of the structures above would predict a linear geometry for the \(\ce{BeX2}\) molecule. Together the three resonance structures suggest partial double-bond character in the Be-X bond, which results in an intermediate bond length between a single and double bond.
There are issues with each of these resonance structures. The structure on the left would predict only four electrons around \(\ce{Be}\); thus, the atom does not fulfill the octet rule. The structure on the left suggests multiple bonds for the halogen (\(\ce{X}\)) and high separation of charge with formal charge on each atom. The structure in the middle is a mix of these problems. None of these situations is ideal according to Lewis theory. Further, experimental data is not consistent with any of these structures or their resonance hybrid (except in the case of \(\ce{BeCl2}\) at very high temperatures).
It turns out that the monomer of \(\ce{BeX2}\) does exist, but only at very high temperatures and low pressures. Even under extreme conditions, the monomer is not particularly stable due to the electron deficiency around \(\ce{Be}\).
BeF2
At ambient temperature and pressure, BeF2 is a solid that looks similar to quartz (Figure \(\PageIndex{1}\)) The Be is four-coordinate with tetrahedral geometry; each F is two-coordinate and the Be-F bond length is 1.54 Å. This structure is possible due to an extended 3-dimensional network in the solid where adjacent BeF2 units are bonded to one another, as shown in Figure \(\PageIndex{1}\).

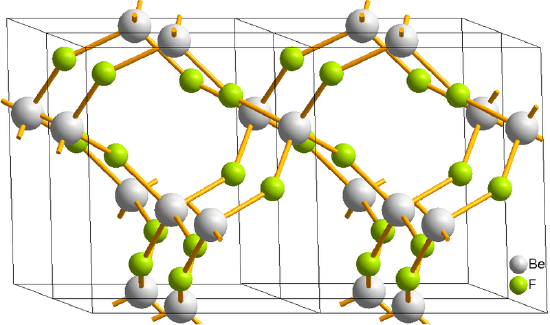
In the liquid phase, \(\ce{BeF2}\) has a fluctuating tetrahedral structure where Be and F ions exchange. The vapor phase is reached at temperatures higher than 1000 °C (at ~ 1 atm). In the vapor phase, \(\ce{BeF2}\) exists as a monomer with linear geometry and a bond length of 1.43 Å, consistent with a double bond between \(\ce{Be}\) and \(\ce{F}\).
BeCl2
At ambient temperature and pressure, \(\ce{BeCl2}\) is a solid. As in \(\ce{BeF2}\) described above, \(\ce{BeCl2}\) has four-coordinate, tetrahedral Be and two-coordinate Cl. In contrast to BeF2, solid BeCl2 is a 1-dimensional polymer consisting of edge-shared tetrahedral.
In the gas phase, BeCl2 exists as a dimer with two chlorine atoms bridging two Be atoms. In the dimer, the Be atoms are 3-coordinate. Bridging Cl atoms are two-coordinate, while terminal Cl atoms are one-coordinate. At higher temperatures in the vapor phase, the linear monomer also exists.
Boron (\(2s^22p^1\))
Prediction based on Lewis structures:
Lewis structures of \(\ce{BH3}\) and \(\ce{BF3}\) were described in Exercise 3.1.2, and are drawn again below for convenience.

Boron trihalides
Boron trihalides, like \(\ce{BF3}\), have properties that are largely predicted by Lewis structures and VSEPR theory. The Lewis structure for \(\ce{BF3}\) includes several resonance structures. The structure with only single bonds is the most common representation for this molecule because the charge separation shown in the other structures is considered to be unfavorable. The highly polarized B-F bond has a dipole moment that lies opposite to the indicated formal charges shown in the resonance structures with double bonds between boron and fluorine.
The resonance hybrid of \(\ce{BF3}\) predicts partial double bond character between boron and fluorine, thus a bond length shorter than a single bond. Using the Lewis structures and VSEPR theory, we would predict a trigonal planar geometry around boron. In fact, the actual structure of \(\ce{BF3}\) is a monomer with trigonal planar geometry and with bond length that is shorter than a single bond. The case is similar to structures of other boron trihalides as well.
Boron trihalides are electron deficient at the boron center and react readily with Lewis bases. In other words they are strong Lewis acids (electrophiles).
Boron trihydride (BH3 is really B2H6)
The properties of boron trihydride (\(\ce{BH3}\)) are not predicted by the simple predictions made through Lewis structures and VSEPR. The monomer, BH3, is not stable, but when dissolved in the presence of a Lewis base, BH3 can form a stable acid-base adduct. In its pure form, the compound actually exists as a dimeric gas with a molecular unit of B2H6 (try drawing a valid Lewis structure for that!). Its unexpected structure includes two H's that bridge the two boron atoms in 3-center-2-electron bonds. You can read more about B2H6 on the Wikipedia page for Diborane(6). The unique bonding observed for boron is described more in Chapter 8 and Chapter 15.


