2.2.1: Particle in a Box
- Page ID
- 155175
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The particle in the box is a model that can illustrate how a wave equation works. Although it does not represent a real situation, we can limit our model to just one dimension (the x-dimension, for instance) such that the Schrödinger equation becomes significantly simplified. Despite being unrealistic, this simplification is quite useful for gaining an understanding of the Schrödinger equation.
The model of a particle in a box
The particle in the box is a hypothetical situation with a particle trapped in a one-dimensional “box”. Let’s not get hung-up on the fact that the common object called a “box” is typically an object with three dimensions instead of just one dimension. And let’s also not get hung up on the word “particle”. This is a particle that has properties of a wave…so it is unlike the macroscopic particle that you’re probably imagining. This “box” is more like a line, or an x-axis; it is just a one-dimensional space in which a particle-wave is trapped.
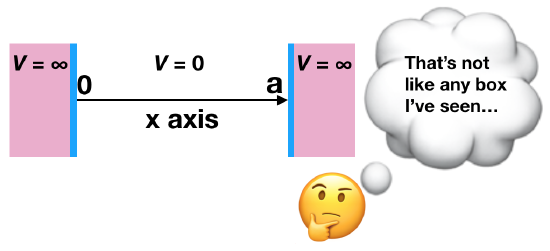
The particle-wave can only exist inside the walls (where \(0<x<a\)), along the x axis in the figure shown above. In terms of energy, the potential energy is zero (\(V=0\)) because the particle is in an energetically-favorable position here. On the other hand, outside the box, the particle cannot exist and the potential energy is infinitely large (\(V=\infty\)) outside the walls (where \(x<0\) or \(x>a\)). This means that it is infinitely unfavorable for the particle-wave to exist outside the box, and so it never does. The particle-wave is trapped between the walls, along the 1-dimensional \(x\) axis, and there are no forces acting on the particle-wave inside this “box”.
The Schrödinger wave equation for a particle in a box
The particle in a box model lets us consider a simple version of the Schrödinger equation. Before we simplify, let's take another look at the full Hamiltonian for a particle-wave in three dimensions (see equation 2.2.2) and the simplest form of the Schrödinger equation (see equation 2.2.1). Both of these equations are described in the previous section and are written below for convenience.
The Schrödinger Equation (from equation 2.2.1): \(\hat{H}\psi = E\psi\)
The Hamiltonian in three dimensions (from equation 2.2.2):
\[\hat{H}=\dfrac{-h{^2}}{8\pi{^2}m_e}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)-\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}\nonumber \]
In the particle in a box model, there is only one dimension, \(x\). Because the \(y\) and \(z\) values are zero, we can drop \(y\) and \(z\) out of our Hamiltonian equation. And, since \(V=0\) inside the box, we can drop the whole part of the Hamiltonian equation that describes the potential energy (\(\frac{-Ze^2}{4\pi{}\epsilon_0{r}}\)). This leaves us with a much simplified Hamiltonian operator, which we can then use to write the Schrödinger wave equation for a particle moving in one dimension. One last thing we'll do is use a more general value \(m\) for the mass of the particle, rather than \(m_e\) that specifically represents the mass of an electron. The Schrödinger equation for a particle-wave in a one-dimensional box is:
\[\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}}\right) = E\psi \label{1DSchr} \]
Follow the steps that were described in the last paragraph to find Equation \ref{1DSchr} from equation 2.2.1 and 2.2.2. In other words, derive the Schrödinger Equation for the particle in a box given the three-dimensional Hamiltonian and Schrödinger Equations.
- Answer
-
Here is the Hamitlonian Equation for in three dimensions.
\(\hat{H}=\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)}-\textcolor{blue}{\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}\)
There are two parts to this equation: the kinetic energy contribution and the potential energy contribution. While the first part of this expression, \(\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)}\), is the kinetic energy contribution, the second part of the expression, \(\textcolor{blue}{-\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}\), is the potential energy (\(V\)) contribution.
(1) Simplify the expression for kinetic energy
Your particle-wave is moving in only one dimension. We can arbitrarily choose the dimension \(x\). This means that \(x\) is a variable and will have some value from \(0\) to \(a\). On the other hand, the particle does not move in the other two dimensions, \(y\) and \(z\). You can assign the position of the particle along \(x\) and \(y\) axes as zero or you can just understand that they do not exist in any significant capacity in our 1-D space. Either way, you can just drop them out of the kinetic energy part of the Hamiltonian, as so:
When \(y=z=0\) and the particle-wave only exists/moves in the \(x\) dimension, \(\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}+\dfrac{\partial{^2}}{\partial{y^2}}+\dfrac{\partial{^2}}{\partial{z^2}}\right)}\) = \(\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}\right)}\)
And the overall Hamiltonian is simplified:
\(\hat{H}=\textcolor{red}{\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}}{\partial{x^2}}\right)}-\textcolor{blue}{\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}\)
(2) Simplify the expression for potential energy (\(V\)).
The particle's potential energy inside the box is zero (\(V=0\)). Therefore, \(\textcolor{blue}{V=-\dfrac{Ze^2}{4\pi{}\epsilon_0{r}}}=0\). We can simply drop the potential energy portion from the Hamiltonian because its value is zero.
The simplified Hamiltonian is now:
\(\hat{H}=\textcolor{red}{\dfrac{-h^2}{8\pi^2m}\left(\dfrac{\partial{^2}}{\partial{x^2}}\right)}\)
(3) Substitute the simplified Hamiltonian into the Schrödinger Equation.
The Schrödinger is: \(\textcolor{red}{\hat{H}}\psi = E\psi\)
When the simplified Hamiltonian is substituted into this equation, the result is the 1-D Schrödinger Equation \ref{1DSchr}.
\(\textcolor{red}{\left(\dfrac{-h{^2}}{8\pi{^2}m}\left(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}}\right)\right)} = E\psi\)
The wavefunction of a one-dimensional wave
Although we've simplified the Schrödinger Equation by considering the particle in the box, Equation \ref{1DSchr} may still look mysterious to you. But it's simpler than you might realize. Let's unpack it! Here we'll go through the steps of deriving the 1-dimensional wavefunction for the particle in a box. We won't try to derive a three-dimensional wavefunction for a "real" electron, but when you understand how to find the 1-dimensional wavefunction, and what it tells us, then you can conceptually extend this to understand what the wavefunction tells us about electrons in three dimensions.
Let's dissect Equation \ref{1DSchr}. Here it is again for reference:
\[\textcolor{green}{\dfrac{-h{^2}}{8\pi{^2}m_e}}\left(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}}\right) = \textcolor{green}{E}\psi\nonumber \]
The expression \(\textcolor{green}{\frac{-h^2}{8\pi^2m_e}}\) is just a negative constant. This negative constant is multiplied by the second derivative of the wavefunction in the expression above. And \(\textcolor{green}{E}\) is a constant multiplied by that same function. We can rearrange this equation as follows:
\[\dfrac{\partial{^2}\psi(x)}{\partial{x^2}} = \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\psi = -\textcolor{green}{C}\psi \label{Schrx} \]
where \(C\) is just the constant; \(\textcolor{green}{C}=\textcolor{green}{\dfrac{8\pi{^2}m_eE}{h{^2}}}\)
To an expert in the mathematical field of Differential Equations, this expression \ref{1DSchr} follows a familiar pattern that makes it easy to translate. If you're not an expert in differential equations, that is OK; you'll just have to bear with this while things get a little "hand-wavy" and try Exercise \(\PageIndex{2}\) to prove it to yourself that the following "hand waviness" is true. An expert in differential equations could tell you that when the second derivative of a function is equal to a negative constant times that same function, the function can be written in terms of \(sin\) and \(cos\), as shown in Equation \ref{wf1} (that was the hand-wavy part...see, not so bad):
\[\psi=A\sin(rx) + B\cos(sx) \label{wf1} \]
\(A, B, r,\) and \(s\) are constants in Equation \ref{wf1}. This expression is useful because it is in a form that we could plot with a graphing program (or calculator). However, to do so we must know the constants \(A, B, r,\) and \(s\).
What are \(r\) and \(s\)?
If we substitute expression \ref{wf1} into Equation \ref{1DSchr} and solve for r and s, we find the expressions below.
\[r=s=\sqrt{2m_eE}\left(\frac{2\pi}{h}\right) \label{rs} \]
This shows us that r and s are equal and constant; we know the values for \(\pi, h,\) and \(m_e\), and we can solve for the constant \(E\).
Show that Equation \ref{wf1} is true in the case that Equation \ref{Schrx} ( \(\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi \)) is true. Also consider Equation \ref{rs} (\(r,s\) are constants and \(r=s\)) and explain why the constant \(r\) must equal \(s\).
To do this problem, you'll also need to know the basic differentiation rules of \(\sin\) and \(\cos\) functions, given below for convenience.
Differentiation Rules for \(sin\) and \(cos\):
\(\frac{d}{dx}\big(\sin(rx)\big)=r\cos(rx)\), where r is a constant.
\(\frac{d}{dx}\big(\cos(rx)\big)=-r\sin(rx)\), where r is a constant.
- Answer
-
You can show that \ref{wf1} is true by substituting \ref{wf1} back into Equation \ref{Schrx}; in other words take the second derivative of the function, \(\psi=A\sin(rx) + B\cos(sx)\) to show that \(\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi \). \(C, r,\) and \(s\) are arbitrary constants, and \(r=s\). The actual value of these constants is irrelevant for this problem. Here is one way to approach the problem:
(1) Substitute \(\textcolor{red}{\psi=A\sin(rx) + B\cos(sx)}\) into \(\textcolor{blue}{\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi} \).
\(\textcolor{blue}{\frac{\partial{^2}}{\partial{x^2}}}\left(\textcolor{red}{A\sin(rx) + B\cos(sx)}\right)= \textcolor{blue}{-C}\textcolor{red}{\psi} \)
(2) Take the first and second derivative of \(\textcolor{red}{A\sin(rx) + B\cos(sx)}\).
The result of taking the first derivative...
\(\textcolor{blue}{\frac{\partial{}}{\partial{x}}}\left(\textcolor{green}{r}\textcolor{red}{A\cos(rx) - \textcolor{green}{s}B\sin(sx)}\right)= \textcolor{blue}{-C}\textcolor{red}{\psi} \)
...and the second derivative...
\(\textcolor{green}{-r^2}\textcolor{red}{A\sin(rx)} - \textcolor{green}{s^2}\textcolor{red}{B\cos(sx)} = \textcolor{blue}{-C}\textcolor{red}{\psi}\)
This is where we see that the only way \(\psi=A\sin(rx) + B\cos(sx)\) is if we can factor the values \(r^2\) and \(s^2\) out of the left side. We have a hint that \(r=s\) from the discussion above and Equation \ref{rs}. Now we see that this is a necessary condition for the expression \(\textcolor{green}{-r^2}\textcolor{red}{A\sin(rx)} - \textcolor{green}{s^2}\textcolor{red}{B\cos(sx)} = \textcolor{blue}{-C}\textcolor{red}{\psi}\) to be true.
(3) Simplify
If \(r=s\), then \(r^2=s^2\) and we can replace s with r in the equation above, as so...
\(\textcolor{green}{-r^2}\textcolor{red}{A\sin(rx)} - \textcolor{green}{r^2}\textcolor{red}{B\cos(sx)} = \textcolor{blue}{-C}\textcolor{red}{\psi}\)
Now, we can factor the constant, \(-r^2\) out of the left side of this expression,
\(\textcolor{green}{-r^2}\left(\textcolor{red}{A\sin(rx) + B\cos(sx)}\right) = \textcolor{blue}{-C}\textcolor{red}{\psi}\)
Now we see that \(\psi=A\sin(rx) + B\cos(sx)\) when \(-C=-r^2\). In other words, we have shown that \(\psi=A\sin(rx) + B\cos(sx)\) is true.
Why is this a useful exercise?
Although it is difficult to explain the derivation of the expression \(\psi=A\sin(rx) + B\cos(sx)\) without differential equations and only knowing that \(\frac{\partial{^2}\psi(x)}{\partial{x^2}}=-C\psi \), to show this is true is as simple as solving this exercise. This exercise is here to help you review your calculus and to show you that the "hand waving" in the text above is not magic, but it is coming from math that you have seen in your calculus courses. Math is crucial for explaining the nature of the universe! Eat your vegetables and practice your math.
*Complete Exercise \(\PageIndex{2}\) before attempting this one.
Derive the expression for r below (from Equation \ref{rs}) using the 1-D wavefunction (\ref{wf1}: \(\psi=A\sin(rx) + B\cos(sx) \)) and the 1-D Schrödinger equation (\ref{1DSchr}: \(\left(\frac{-h{^2}}{8\pi{^2}m_e}\left(\frac{\partial{^2}\psi(x)}{\partial{x^2}}\right) = E\psi\right)\)).
\(r=\dfrac{2\pi}{h}\sqrt{2m_eE}\)
- Answer
- The steps below could be carried out in a different sequence:
(1) Rearrange
Let's move all constants to the right side of \ref{1DSchr} so that we arrive at the expression that is shown in part of Equation \ref{Schrx} .
\(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}} = \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\psi\)
(2) Take the second derivative of \(\psi\), which we found in Exercise \(\PageIndex{2}\).
\(\dfrac{\partial{^2}\psi(x)}{\partial{x^2}} =\textcolor{green}{-r^2}\left(\textcolor{red}{A\sin(rx) + B\cos(sx)}\right) = \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\textcolor{red}{\psi}\)
And since \(\textcolor{red}{\psi=A\sin(rx) + B\cos(sx)}\), we can simplify this by dividing both sides by \(\psi\) (or by \(A\sin(rx) + B\cos(sx) \)).
**recall that \(s=r\). So, you could have substituted \(r\) for \(s\) in the expression above, and you'd still be on the right track.
\(\textcolor{green}{-r^2}= \textcolor{green}{\dfrac{-8\pi{^2}m_eE}{h{^2}}}\)
(3) Solve for r (*we already showed \(r=s\) in the Exercise \(\PageIndex{2}\)).
\(\textcolor{green}{r} = \sqrt{\dfrac{8\pi{^2}m_eE}{h{^2}}} = \dfrac{2\pi}{h}\sqrt{2m_eE}\)
What are \(A\) and \(B\)?
We can find the possible values of \(A\) and \(B\) by looking at the possible extremes for the value of \(x\). In our model in Figure \(\PageIndex{1}\), we can see that x can have values from \(0\rightarrow a\). The two extremes, where \(x=0\) and \(x=a\), lie at the walls of the box. The electron cannot exist beyond these values because it is trapped inside the walls, so its wavefunction must be zero at \(x=0\) and \(x=a\).
The case where \(x=0\) can help us find the value of \(B\). We just said that the wavefunction must be zero where \(x=0\). This means:
\[\psi_{x=0} = A\sin(rx) + B\cos(sx) = A\sin(0) + B\cos(0) = 0 \nonumber \]
Because \(A\sin(0)=0\), the expression can be simplified to:
\[\psi_{x=0} = B\cos(0) = B(1) = 0 \nonumber \]
Now we can see that there is only one possible value for the constant, \(B\), that would allow this expression to be true, \(B=0\). And since \(B\) is constant then it will always be zero despite the value of \(x\). This simplifies our 1-D wavefunction:
\[\psi=A\sin(rx) \label{wf2} \]
The case where \(x=a\) can help us find the value for \(A\). Since the wavefunction must be zero where \(x=a\):
\[\psi_{x=a} = A\sin(rx) = A\sin(ra) = 0 \nonumber \]
In this case, \(A\) cannot be zero because if both A and B are zero, the wavefunction is zero at all values of \(x\), and so our wavefunction would not exist inside the box. So, let's assume A is not zero. Then, it must be the case that
\[\sin(ra)=0 \nonumber \]
and then because of the way that \(\sin\) functions work, the quantity \(ra\) must be an integer value of \(\pi\) if \(\sin(ra)=0\).
\[ra = \pm n\pi \nonumber \]
where \(n\ = 1, 2, 3...\) any non-zero integer. We can ignore negative values here since both positive and negative values of \(r\) will give the same value for \(\sin(ra)\). We can then solve for r:
\[r=\frac{n\pi}{a} \label{r} \]
and substitute the value \(r=\dfrac{n\pi}{a}\) into Equation \ref{wf2} to get:
\[\psi = A\sin\left(\frac{n\pi{x}}{a}\right) \label{wf3} \]
Recall that the square of the wavefunction (\(\psi^2\)) gives the probability of finding the electron anywhere in space. In our model, the probability of finding the particle-wave inside the box is unity (it is 1). Mathematically, this is the normalizing requirement (expressed as \(\int \psi_A \psi_A^* d\tau=1\)), which can be solved to find the value of A.
\[A = \sqrt{\frac{2}{a}} \nonumber \]
Now, we can substitute the value of \(A\) into expression \ref{wf3}, and we have a wavefunction that can be visualized using any graphing program/calculator!
\[\psi=\sqrt{\frac{2}{a}}\left(\sin\left(\frac{n\pi{x}}{a}\right)\right) \label{wf4} \]
What is the energy (E) of a particle in the box?
So, now you can see how a 1-D wavefunction can be solved. But how do we find the E of the electron from this? Well, in order to not distract you earlier, we skipped over a very simple way to do this. The E falls right out of the equations you just saw. We can set the two expressions we found above for the constant \(r\), (equations \ref{rs} and \ref{r}) equal to one another and then solve for E:
\[r=\dfrac{n\pi}{a}=\sqrt{2mE}\left(\dfrac{2\pi}{h}\right) \nonumber \]
\[E=\frac{n^2h^2}{8ma^2} \label{E} \]
Expression \ref{E} can be used to calculate the energy of a particle in a one-dimensional box of length \(a\), given its integer energy level, \(n\). Here we can see that the energy is quantized because \(n\) is an integer (\(n=1,2,3...\)). In other words, \(n\) is a quantum number.
Making sense of the particle in a box: plotting the 1-D \(\psi\) and \(\psi^2\).
No matter whether you're dealing with a 1-dimensional or 3-dimensional wave equation, the wavefunction itself (\(\psi\)) describes the particle's wave properties. This \(\psi\) doesn't have actual physical meaning, so it's hard to imagine what it "looks like" other than just plotting its function. However, the probability of finding the particle-wave at any specific position along the x-axis between \(x=0\) and \(x=a\) is more physically meaningful. The probability of finding the particle is proportional to the square of the wave function, which is represented by either \(\psi^2\) or, sometimes, \(\psi\psi^*\). The plots of the functions for \(\psi\) and \(\psi^2\) for the first three possible values of \(n\) are shown below in Figure \(\PageIndex{2}\). You could create plots similar to these simply by plotting the function shown in Equation \ref{wf4}. To plot, you just need to assign a value of \(n\), and it is convenient to assign the length of the box as \(a=1\). The plot generated would have the general ratio of \(\frac{x}{a}\) on the x axis, and thus would be relevant for any length box.
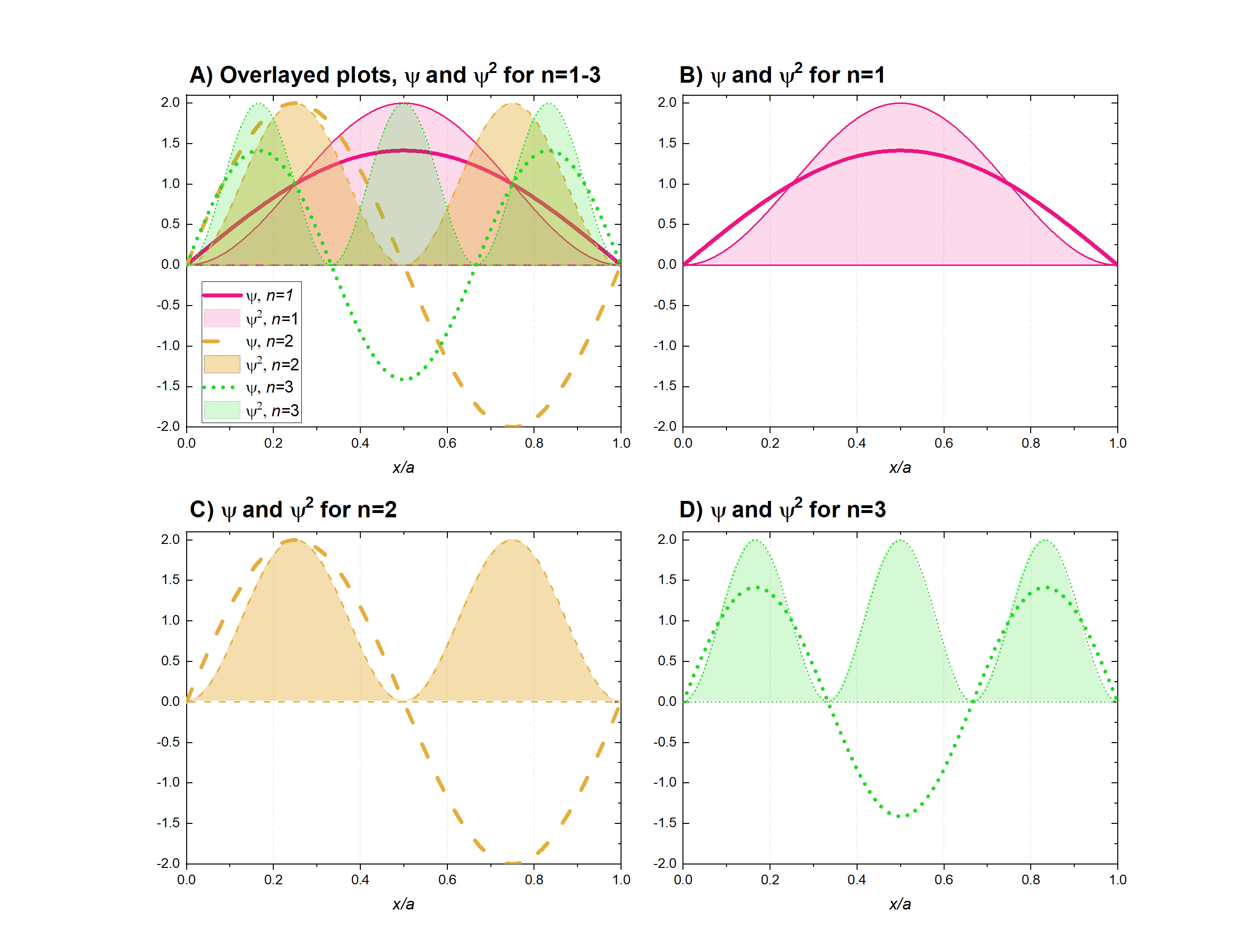
The graphs above represent "solutions" to the wave function. For example, the solution \(n=1\) gives the plot shown in Figure \(\PageIndex{2}\) B. The solution of \(n=2\) is plotted in Figure \(\PageIndex{2}\) C, and so on. These values for \(n\) are some of the possible solutions to the 1-dimensional \(\psi\), and they yield descriptions of the wave behavior and probability of finding a particle in 1-dimensional space.
How does this apply to atoms?
The 1-dimensional particle in a box does not represent a real situation; but rather, it is a simple model that we can use to understand a more complex system, like a electron orbiting the nucleus in three dimensions. It's useful to recognize the analogies here that might represent something familiar in a real situation.
\(x=0\) is analogous to the nucleus in an atom. Here in the particle in a box model, \(\psi=0\) and there is zero probability of finding an electron. When this is extended to an atom, this position is analogous to the nucleus (at the origin of a coordinate system where \(x=y=z=0\). A 3-dimensional \(\psi\) is also zero at the nucleus and the electron cannot exist there; also, \(\psi\) approaches zero as it approaches this position in both the particle in a box model and in a more realistic case of an electron in an atom.
\(x=a\) is analogous to a boundary surface far from the nucleus. In the particle in a box model, the 1-dimensional \(\psi\) is zero at \(x=a\). This is analogous to an electron's \(\psi\) approaching zero as it gets further from the nucleus. There will be a more in depth description of boundary surface in the next section (2.2.2). You already know this as the outermost surface of an electron orbital. One minor but notable difference between the 1-dimensional particle in a box and the case of a real atom is that the \(\psi\) in three dimensions approaches but never quite reaches zero as distance from the nucleus increases, while \(\psi=0\) for \(x=a\) in the more simple case of a 1-dimensional particle in a box.
A change in sign of the \(\psi\) (and where both \(psi=0\) and \(\psi^2=0\)) is a node. In both the 1-dimensional particle in a box model and in the more realistic 3-dimensional case, a node is found where the \(\psi\) changes sign. At this point, \(\psi=\psi^2=0\); in other words there is zero probability of finding the particle or electron at these points. It is easy to spot these points in the plots above because the wave function crosses the x-axis and the \(\psi^2\) meets zero.
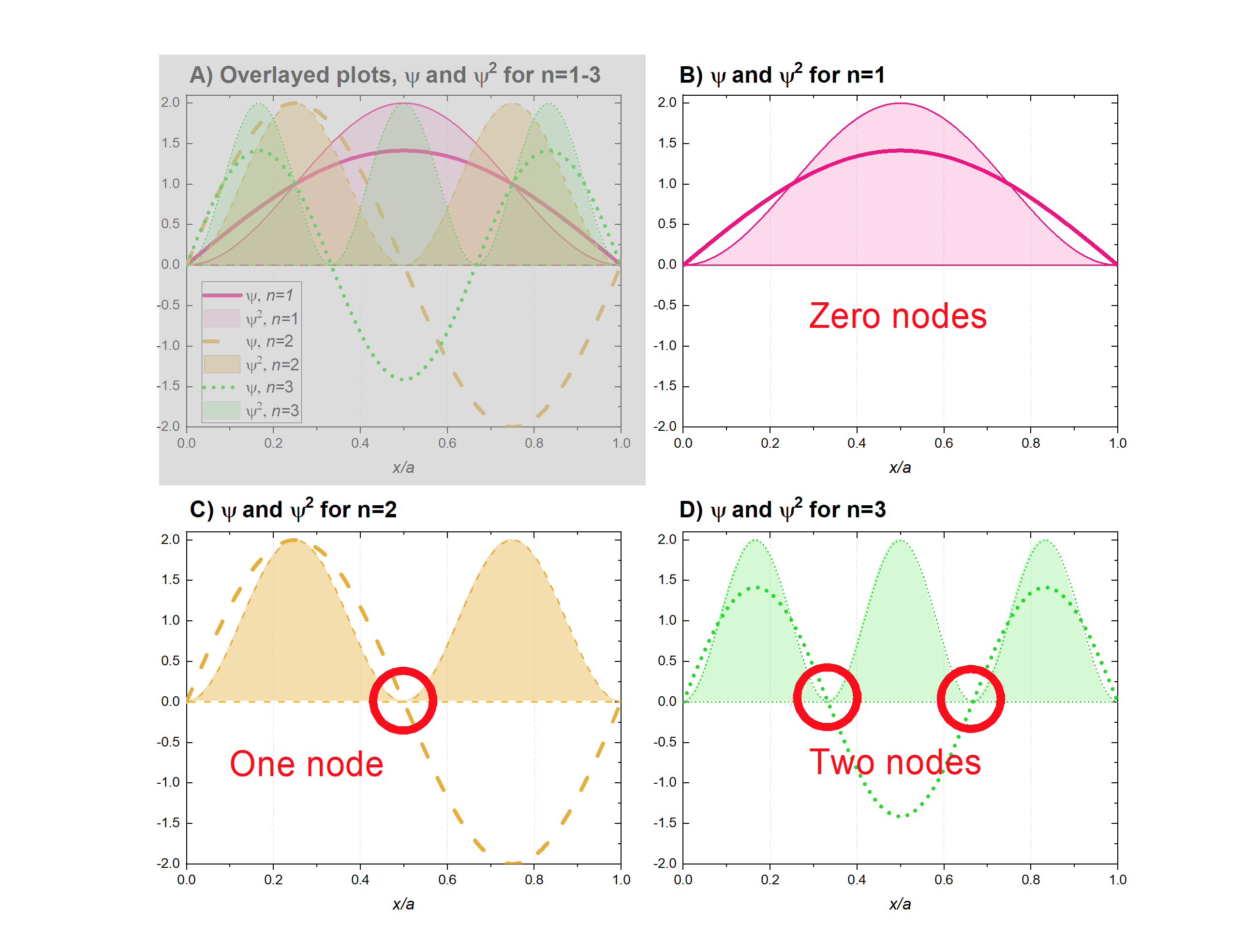
Identify the points on plots B, C, and D in Figure \(\PageIndex{2}\) that are nodes. How many nodes are there for \(n=1, n=2,\) and \(n=3\)?
- Answer
-
The nodes are annotated with red circles on the figure below. Panel B (\(n=1\)) has zero nodes. There are two points where \(\psi=0\) in the case of \(n=1\), but these points are at the walls of the box and they are not nodes. The walls of the box are analogous to the nucleus and the boundary surface of an electron orbital. Panel C (\(n=2\)) has one node where the \(\psi\) crosses zero. Panel D (\(n=3\)) shows two nodes.
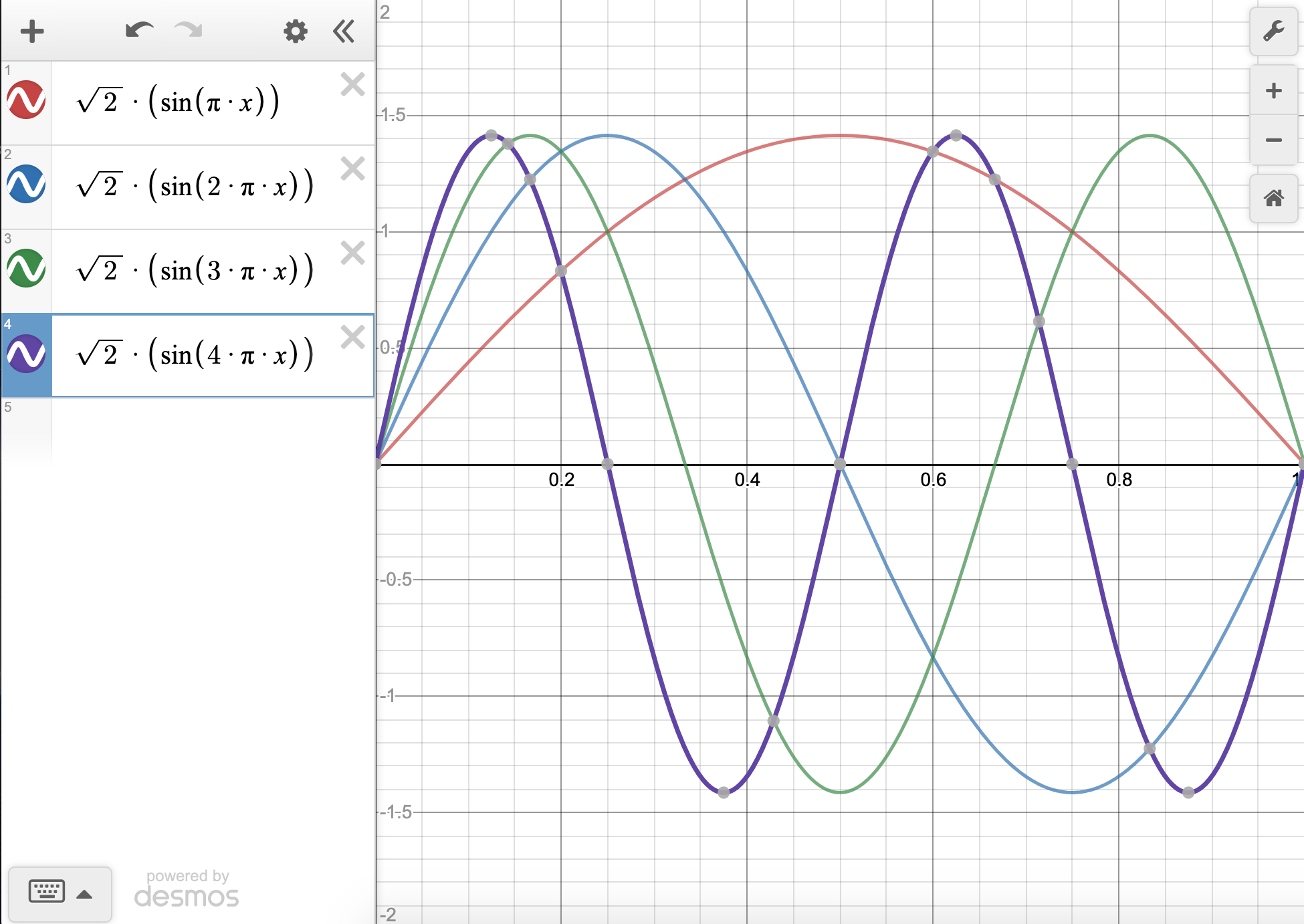
Use a graphing program to plot the 1-dimensional \(\psi\) and \(\psi^2\) for \(n=1,2,3,4\). How many nodes are there for \(n=4\)? Is this expected? Predict how many nodes we should expect for \(n=5\).
You can use any plotting program to do this, and if you aren't familiar with any, try this one: Desmos
- Answer
-
You can use any plotting program to do this. This is the function you should plot (it is Equation \ref{wf4}):
\(\psi=\sqrt{\frac{2}{a}}\left(\sin\left(\frac{n\pi{x}}{a}\right)\right)\)
For n=1: Assign a value of \(n=1\), as stated in the problem. In the text above, it also states that it is convenient to assign a value of \(a=1\). Assigning these values results in the following function:
\(\psi=\sqrt{\frac{2}{1}}\left(\sin\left(\frac{1\pi{x}}{1}\right)\right)\) and simplifying leads to \(\psi=\sqrt{2}\left(\sin\left(\pi{x}\right)\right)\)
For n=2,3,4 you would repeat the process above. You will get the following functions:
For n=2: \(\psi=\sqrt{2}\left(\sin\left(2\pi{x}\right)\right)\)
For n=3: \(\psi=\sqrt{2}\left(\sin\left(3\pi{x}\right)\right)\)
For n=4: \(\psi=\sqrt{2}\left(\sin\left(4\pi{x}\right)\right)\)
In a program like Desmos, you need to input the function correctly. It's useful to know the code for at least one graphing program. For Desmos, and most others, you can find help online. For example, the correct input for Desmos for the n=4 case is sqrt(2)*(sin(4*pi*x)). But, you have to type it in because copy/paste doesn't work. You'll also want to display your graph only from \(x=0\) to \(x=1\) by hitting the settings button (a little wrench in the upper right corner) and changing the x scale. Go ahead and change the y scale too, to \(y=-2\) to \(y=2\). If you do this, you should get something that looks like this:
To graph the square of each wavefunction, you'd just square the functions that we just plotted:
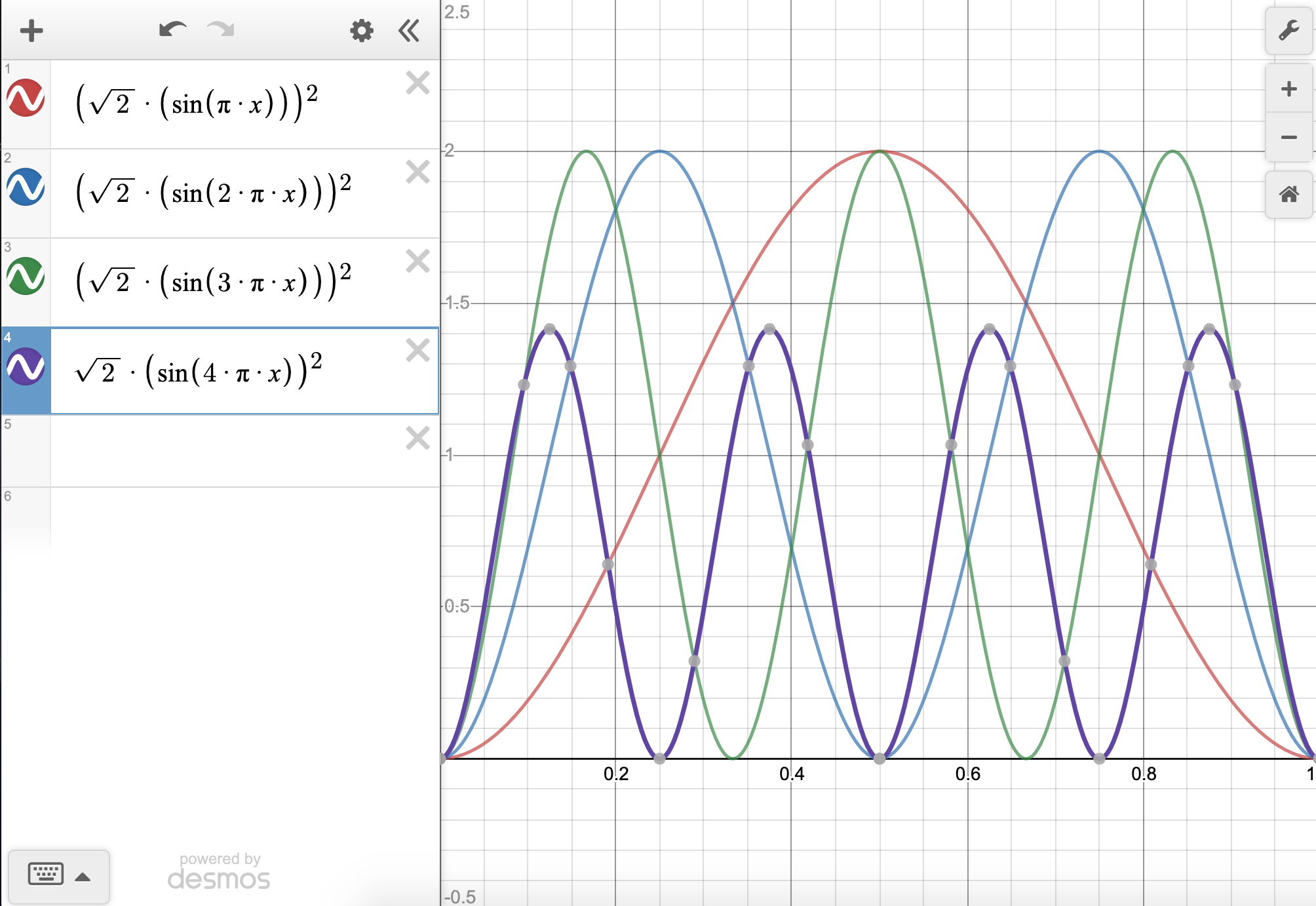
In both the case of \(\psi\) and \(\psi^2\), the \(n=4\) function shows three nodes (see the bolded purple line, where nodes are tiny grey spots on the axis). This follows a pattern that you might have noticed with the cases of \(n=1,2,\) and \(3\) where the number of nodes is \(n-1\) (nodes = \(n-1\)). We should expect three nodes for \(n=4\) based on this pattern, and four nodes for \(n=5\).
In the next section, we will extend these ideas qualitatively to three dimensions. While there is only one quantum number in one dimension, there are three quantum numbers in three dimensions that (when combined) give discrete descriptions of an electron in three-dimensional space (plus a fourth quantum number that explains other properties of the electron).


