3.2: Compounds of the Alkali Metals

The chemistry of the alkali metals is dominated by the stability of the +1 oxidation state and the noble gas configuration of the M⁺ cation. The alkali metals all have low first ionization energies (Table \(\PageIndex{3}\).6) but very high second ionization energies.

Table \(\PageIndex{3}\).6: First ionization potentials for the alkali metals.

Element	1^st ionization energy (kJ/mol)
Li	526
Na	502
K	425
Rb	409
Cs	382

As a consequence of the stability of M⁺, the Group 1 metals have the least variation in chemistry of the any Group in the periodic table. The only exceptions are the subtle trends that exist for lithium due to its small size (Table \(\PageIndex{3}\).7). All of the metals are more electropositive than hydrogen (Table \(\PageIndex{3}\).8).

Table \(\PageIndex{3}\).7: Radii of alkali metals. N.B. Some values are unknown.

Element	Atomic radius (Å)	Ionic radius (Å)	Covalent radius (Å)	Van der Waals radius (Å)
Li	1.52	0.68	1.52	1.82
Na	1.86	0.97	1.53	2.27
K	2.31	1.33	1.90	2.75
Rb	2.44	1.47	2.47	-
Cs	2.62	1.67	2.65	-
Fr	-	1.80	2.70	-

Table \(\PageIndex{3}\).8: Pauling electronegativities of Group 1 elements.

Element	Electronegativity
H	2.20
Li	0.98
Na	0.93
K	0.82
Rb	0.82
Cs	0.79
Fr	0.70

Solid State

In the solid state, the compounds of the alkali metals generally form ionic lattices, e.g., \(\ce{Na^{+}Cl^{-}}\). These structures are essentially electrostatic in nature and the lattice energy is usually defined as the enthalpy of formation of the ionic compound from gaseous ions and as such is invariably exothermic.

\[M^+_{(vap)} + X^-_{(vap)} \rightarrow MX_{(s)} \]

In all cases the lattice energies is high and is found to be proportional to the ratio of the charges on the ions and the sum of the ionic radii (\(r\)).

\[ U \propto \dfrac{z^+ z^-}{\displaystyle \sum(r)} \]

The ionic radii for alkali metal cations are given in Table \(\PageIndex{3}\).7; those for common anions are given in Table \(\PageIndex{3}\).9.

Table \(\PageIndex{3}\).9: Ionic radii of common anions.

Anion	Ionic radius (Å)
F^-	1.33
Cl^-	1.81
Br^-	1.96
I^-	2.20
H^-	1.54
O^2-	1.32

The ratio of the ionic radii (r⁺/r^-) neatly defines the structural type observed for alkali metal salts (Table \(\PageIndex{3}\).10). The unit cells for ZnS (zinc blende), NaCl (rock salt), and CsCl are shown in Figure \(\PageIndex{3}\).11, Figure \(\PageIndex{3}\).12, and Figure \(\PageIndex{3}\).13, respectively.

Table \(\PageIndex{3}\).10: Defining MX structural types for alkali metal salts.

r^+/r^-	Structural type	Metal coordination number
0.225 - 0.414	ZnS (zinc blende)	4
0.414 - 0.732	NaCl (rock salt)	6
0.732 -	CsCl	8

Figure \(\PageIndex{11}\): Unit cell structure of a zinc blende (ZnS) lattice.

Figure \(\PageIndex{12}\): Unit cell structure of a rock salt lattice.

Figure \(\PageIndex{13}\): Unit cell of CsCl.

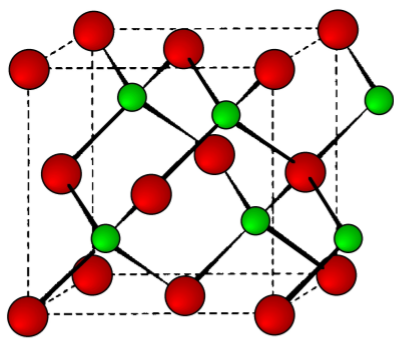
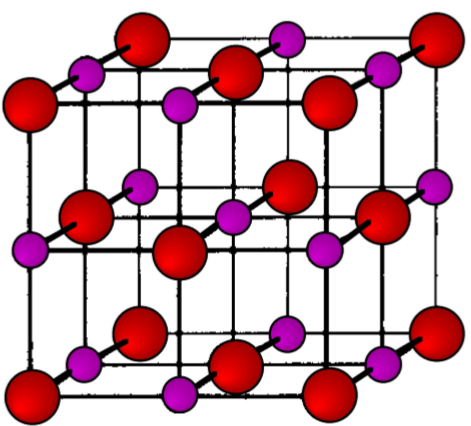
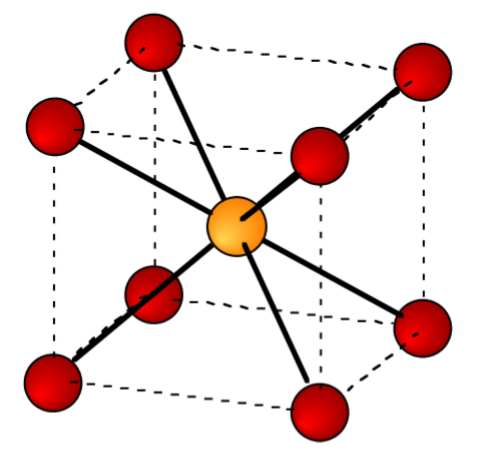
As an example, the structure of KBr can be predicted from the data in Table \(\PageIndex{3}\).7 and Table \(\PageIndex{3}\).9. The ionic radius of K⁺ is 1.33 Å, while that for Br^- is 1.96 Å. The ratio of the ionic radii (r⁺/r^-) is 0.67. Hence, KBr has a NaCl (rock salt) structure.

Exercise \(\PageIndex{1}\): Sodium Hydride

What is the structure of NaH?

Answer

The ionic radius of Na⁺ is 0.97 Å, while that for H^- is 1.54 Å. The ratio of the ionic radii (r⁺/r^-) is 0.67. Hence, NaH has a NaCl (rock salt) structure

Exercise \(\PageIndex{2}\): Rubidium Fluoride

What is the structure of RbF?

Answer

The ionic radius of Rb⁺ is 1.47 Å, while that for F^- is 1.33 Å. The ratio of the ionic radii (r⁺/r^-) is 1.10. Hence, RbF has a CsCl structure.

Complexes

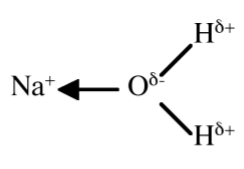
The coordination complexes of the alkali metal cations (M⁺) involve electrostatic, or ion-dipole, interactions (Figure \(\PageIndex{3}\).14) that have no preferred direction of interaction. Thus, the ionic radius of the cation (Table \(\PageIndex{3}\).7) controls the coordination numbers of the metal in its complexes (Table \(\PageIndex{3}\).11).

Figure \(\PageIndex{14}\): A schematic representation of the ion-dipole or electrostatic interaction of Na+ with water.

Table \(\PageIndex{3}\).11: Coordination number for alkali metal ions in aqueous complexes.

Aqua ion	n
[Li(H2O)n]^+	4
[Na(H2O)n]^+	6
[K(H2O)n]^+	6
[Rb(H2O)n]^+	6-8
[Cs(H2O)n.]^+	8

In general the alkali metal ions form complexes with hard donor such as oxygen (H₂O, ROH, RCO₂^-, etc.) or nitrogen (e.g., NH₃, NR₃, etc.). The aquo complexes readily exchange the water for other ligands, (3.13); however, the equilibrium constants are small when the ligand is similar in size to water.

\[ [M(H_2O)_n]^+ + L \leftrightharpoons [M(H_2O)_{n-1}L]^+ + H_2O\]

As a consequence of the low equilibrium constants for monodentate ligands, the alkali metal cations, M⁺, favor coordination to polydentate ligands such as ethylenediaminetetraacetic acid (EDTA, Figure \(\PageIndex{3}\).15), polyethers, and even natural polyesters or polypeptides. In each case the polydentate ligand wraps itself around the cation.

Figure \(\PageIndex{15}\): Structure of ethylenediaminetetraacetic acid (EDTA).

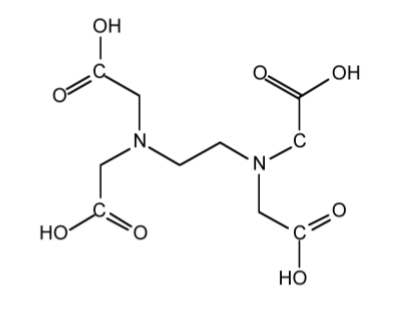
Macrocyclic ligands

Macrocyclic ligands represent a special class of polydentate ligand. They are defined as being a cyclic compound with nine or more members including all the heteroatoms and with three or more donor atoms. and are given the special name of cryptands when they are synthetic bi- and poly-cyclic multidentate ligands. Crown ethers is the name applied to macrocyclic ligands that consist of a ring containing several ether groups. Figure \(\PageIndex{3}\).16 shows several common macrocyclic ligands.

Figure \(\PageIndex{16}\): The structures of some common macrocyclic ligands.

Macrocyclic ligands are generally oxygen or nitrogen donor ligands, and they form highly stable 1:1 complexes with alkali metal ions in which all or most of the coordination sites on the metal are occupied, i.e., [M(L)]⁺ rather than [M(L)(H₂O)_n]⁺. Since the external surface of the macrocyclic ligands comprises of organic residue (e.g., CH₂ groups) the complexes are soluble in organic solvents. Thus, crown ethers are commonly used to solubilize salts (e.g., NaCl) in organic solvents. They have also been used to create solutions of nanoparticles, such as carbon nanotubes (Figure \(\PageIndex{3}\).17), that are ordinarily highly insoluble in common organic solvents (Table \(\PageIndex{3}\).12).

Figure \(\PageIndex{17}\): Representation of the reaction between Na/Hg amalgam, dibenzo-18-crown-6, and puried single walled carbon nanotubes (SWNTs) in toluene and the formation of the [Na(dibenzo-18-crown6)]_n[SWNT] complex. Adapted from R. E. Anderson and A. R. Barron, J. Nanosci. Nanotechnol., 2007, 7, 3436

Table \(\PageIndex{3}\).12: The concentration of Na/dibenzo-18-crown-6 solubilized reduced single walled carbon nanotubes (SWNTs) in various solvents.

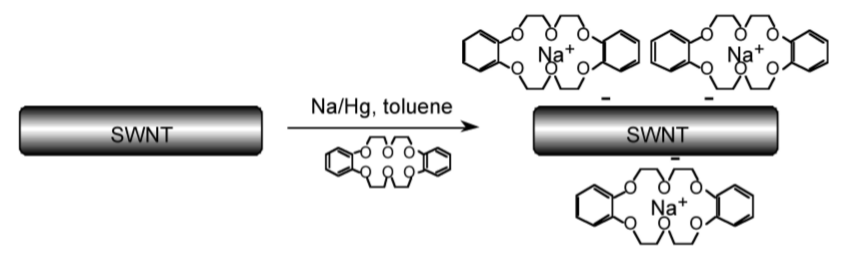
Solvent	SWNT concentration (mg/L)
CH2Cl2	14.05
DMF	11.42
hexane	4.65
toluene	3.79
EtOH	2.37
MeOH	2.37
CHCl3	0.30
H2O	0.10

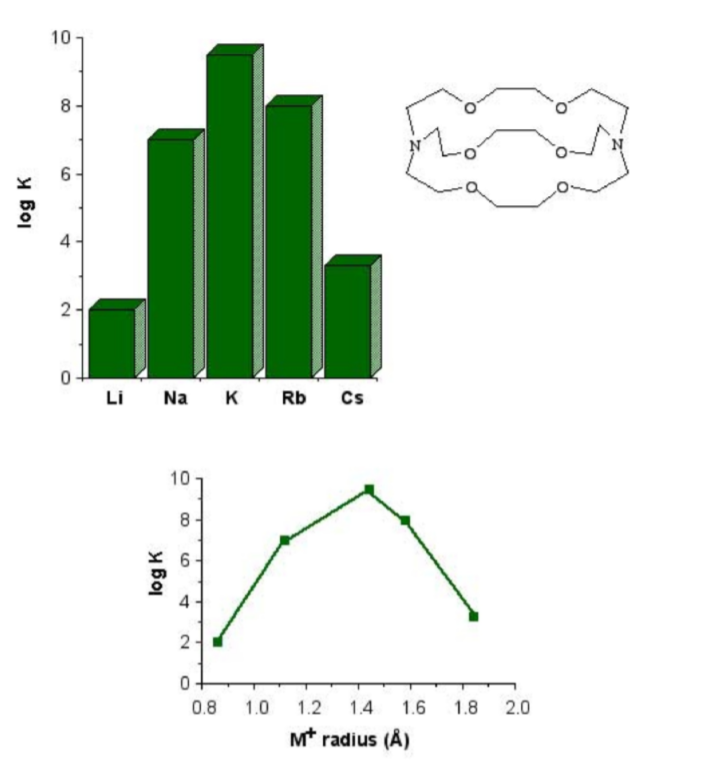
The most important factor in the coordination of various macrocyclic ligands to alkali metal ions is the relative size of the ion and the ligand cavity. For example, 4,7,13,16,21,24-hexaoxa-1,10diazabicyclo[8,8,8]hexacosane is a potentially octa-dentate ligand; however, the binding eciency is very dependant on the identity of the M+ ion (Figure \(\PageIndex{3}\).18). The low binding constant for lithium is probably as a consequence that the ligand would have to distort to coordinate to the small cation. Conversely, the lower equilibrium for caesium is due to its being to large to t completely into the ligand cavity.

Figure \(\PageIndex{18}\): : Relative stability constants (log K) of alkali metal ions to 4,7,13,16,21,24-hexaoxa-1,10diazabicyclo[8,8,8]hexacosane and relationship to the M⁺ ionic radius.

One application of the size effect for macrocyclic ligands is the ability to selectively bind different metals. For example, the 4,7,13,16,21-pentaoxa-1,10-diazabicyclo[8,8,5]tricosane and 4,7,13,16,21,24-hexaoxa-1,10diazabicyclo[8,8,8]hexacosane ligands shown in Figure \(\PageIndex{3}\).19 have very different binding constants to Na⁺ and K⁺, as a consequence of the relative size of the cation and the ligand cavity (Table \(\PageIndex{3}\).13).

Figure \(\PageIndex{19}\): Structure of (a) 4,7,13,16,21-pentaoxa-1,10-diazabicyclo[8,8,5]tricosane [2,2,1] and (b) 4,7,13,16,21,24-hexaoxa-1,10-diazabicyclo[8,8,8]hexacosane [2,2,2].

Table \(\PageIndex{3}\).13: Equilbrium constants for the M+ complexes for macrocyclic ligands with different cavity sizes. The structures of the ligands are shown in Figure \(\PageIndex{3}\).19.

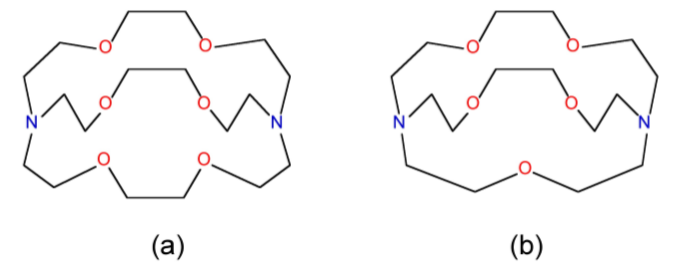
Cation	[2,2,2]	[2,2,1]
Na^+	800	250,000
K^+	250,000	700

Bibliography

1. R. E. Anderson and A. R. Barron, J. Nanosci. Nanotechnol., 2007, 7, 3436.
2. J. M. Lehn, Supramolecular Chemistry: Concepts and Perspectives. VCH (1995).