2.7: The Hydrogen Bond
- Page ID
- 212849
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Hydrogen bonds are formed between a species with a polar Xδ--Hδ+ bond and a species with a lone pair (Yδ-), i.e., Xδ--Hδ+...Yδ-. The most common species for X are oxygen and nitrogen, and to a lesser extent carbon, fluorine, and sulfur. However, as long as the X-H bond is polar then hydrogen bonding is possible. Similarly, the most common Lewis bases that hydrogen bond involve oxygen, nitrogen, and fluorine as the donor atom. Again there are many examples of other atoms, but as long as the atom has a lone pair that is chemically active, hydrogen bonding can occur.
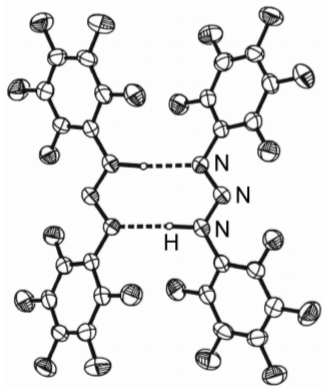
The majority of hydrogen bonds are asymmetrical, that is the hydrogen is closer to one atom than the other (Figure \(\PageIndex{2}\).15), even when X and Y are the same element, i.e., O-H...O. While the typical hydrogen bond involves one Lewis base (lone pair donor), there are many examples where the hydrogen interacts with two Lewis base lone pairs (Figure \(\PageIndex{2}\).16).
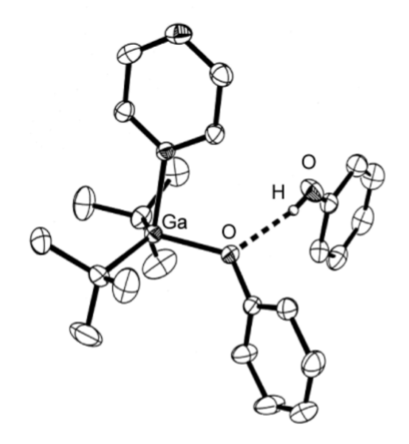
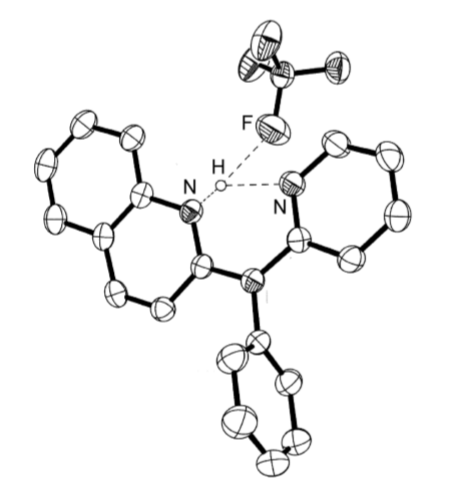
Hydrogen bonds are mostly electrostatic attractions, and as such they are weaker than covalent bonds, but stronger than van der Waal interactions. With bond strengths generally covering the range of 5 50 kJ/mol, the energy required to break a hydrogen bond is comparable to that of thermal motion within the temperature range of 0 200◦C. As a consequence the number of groups involved in hydrogen bonding decreases with increasing temperature, until few hydrogen bonds are observed in the vapor phase. One noted exception is the hydrogen bridged anion [F-H-F]-, in which the strong interaction (243 kJ/mol) is covalent in character involving a three-center molecular orbital bond.
Classes of hydrogen bond
Although hydrogen bonds may be characterized with respect to the X and Y atom, it is more useful to classify them as either intramolecular or intermolecular hydrogen bonds. This is due to the difference in physical and chemical properties between these two classes.
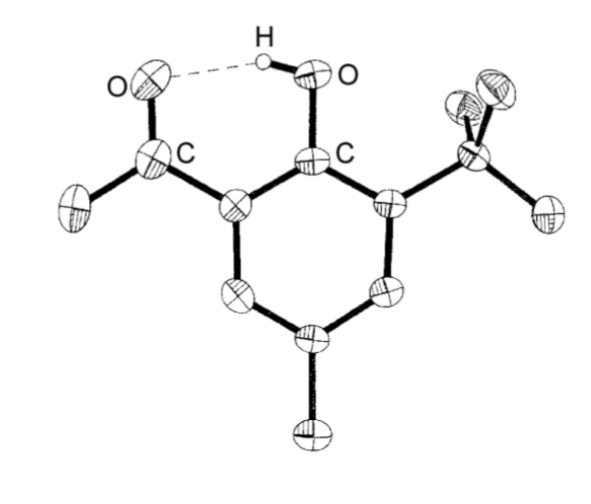
Intramolecular
Intramolecular hydrogen bonds (X-H...Y) arise where the X and Y atoms are in the same molecule (Figure \(\PageIndex{2}\).17).
Intermolecular
If the hydrogen bond (X-H...Y) involves X and Y being from different molecules this is an intermolecular hydrogen bond. Within the range of intermolecular hydrogen bonded compounds there are two sub-categories: those involving discrete molecular species (oligomers) and those resulting in polymeric species.
Carboxylic acids are a typical example of a discrete oligomeric species that are held together by intermolecular hydrogen bonds (Figure \(\PageIndex{2}\).18a). A wide range of structurally analogous compounds also form head-to-tail hydrogen bonded dimers (e.g., Figure \(\PageIndex{2}\).19). In a polymeric hydrogen bonded species every molecule hydrogen bonds but in a random form. As an example, liquid primary alcohols form extended hydrogen networks (Figure \(\PageIndex{2}\).18b). Such an arrangement is labile and as such it is difficult to determine definitive speciation. Liquids that form this type of hydrogen-bonded network are known as associated liquids. In the solid state the networks generally adopt a more ordered structure. For example as is seen in the structure of ice.
Methods of study
The study of the structure arising from hydrogen bonding and the properties exhibited due to the presence of hydrogen bonds is very important.
Diffraction methods
X-raydiffraction of single crystals is the most common structural method employed to determine the presence, effect, and strength of a hydrogen bond. Unfortunately, in order for the location of the hydrogen to be determined with some degree of accuracy, diffraction data of a high quality is needed and/or low temperature (e.g., -196 ◦C) data collection is required. Neutron scattering can be used where very accurate data is required because hydrogen atoms scatter neutrons better than they do X-rays. Figure \(\PageIndex{2}\).20 summarizes the key parameters that are obtained from X-ray (and neutron) diffraction experiments.

Given the electrostatic nature of a hydrogen bond between a polar X-H bond and a Lewis base it is reasonable that the X-H...Y angle (θ) is roughly linear (i.e., 180◦). However, it is not always so and nonlinear interactions are known where steric or conformational restrictions limit the orientation of the X-H bond with respect to Y.
The distance between X and Y, d(X...Y), is less than the sum of the van der Waal radii of X and Y (Table \(\PageIndex{2}\).5). This is in line with the relative strength of these interactions. As would be expected the shorter the X...Y distance the stronger the hydrogen bond.
| X | Y | Sum of van der Waal radii (Å) | Typical X...Y distance (Å) |
| O | O | 2.8 | 2.50-2.69 |
| O | N | 2.9 | 2.75-2.85 |
| N | N | 3.0 | 2.69-2.98 |
The bond distance to hydrogen, d(X-H), is often longer in hydrogen bonded species. For example the O-H distance for an alcohol in the absence of hydrogen bonding is typically 0.97 Å. In contrast, the value typically seen for a hydrogen-bonded analog is 1.05 Å.
Spectroscopy
Spectroscopy is a simple method of comparing hydrogen-bonded systems in particular in the solution or liquid phase.
Infra red and Raman
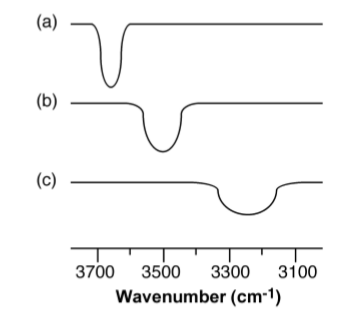
The X-H stretching frequency in the IR (and Raman) spectrum is dependant on the identity of X, i.e., O-H = 3610 - 3640 cm-1 and N-H = 3400 - 3500 cm-1. However, the ν(X-H) is shifted to lower energy (lower frequency) as a consequence of hydrogen bonding. In addition, while non-hydrogen bonded X-H stretches are sharp, the presence of hydrogen bonding results in the peak being broadened. Figure X demonstrates both these effects. The O-H stretch for dilute nBuOH in CCl4 is a sharp peak at 3650 cm-1 due to the lack of hydrogen bonding between the two components (Figure \(\PageIndex{2}\).21a), and the presence of hydrogen bonding between nBuOH and nBuOH is limited by the dilution. By contrast, a dilute solution of nBuOH in Et2O results in a shift to lower frequency and a significant increase of peak width (Figure \(\PageIndex{2}\).21b) as a result of fairly strong O-H...O bonds. Finally, a dilute solution of nBuOH in NMe3 results in a further shift to 3250 cm-1 and a very broad peak (Figure \(\PageIndex{2}\).21c). The broadening of the peaks is due to the distribution of X-H distances within a X-H...Y hydrogen bond.
NMR
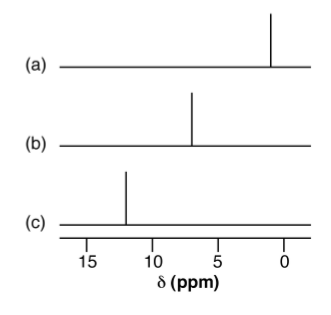
The presence of hydrogen bonding results the shift to higher ppm (lower frequency) of the 1H NMR resonance for the proton. This shift is due to the decrease in shielding of the proton. A dilute solution of nBuOH in CCl4 shows a resonance typical of a non-hydrogen bonded compound (Figure \(\PageIndex{2}\).22a), while that for nBuOH in NMe3 (Figure \(\PageIndex{2}\).22b) shows a significant low field shift. Very strong intra or intermolecular hydrogen bonded species show a very large 1H NMR shift (e.g., Figure \(\PageIndex{2}\).22c).
Effects of hydrogen bonding
Physical effects
The presence of intermolecular hydrogen bonding provides additional attractive forces between molecules. Thus, properties that depend on intramolecular forces are affected.
Liquids with significant hydrogen bonding exhibit higher boiling points, higher viscosity, and higher heat of vaporization (∆Hv) as compared to analogous compounds without extensive hydrogen bonding. For solids the presence of hydrogen bonding results in an increase in the melting point of the solid and an increase in the associated heat of fusion (∆Hf).
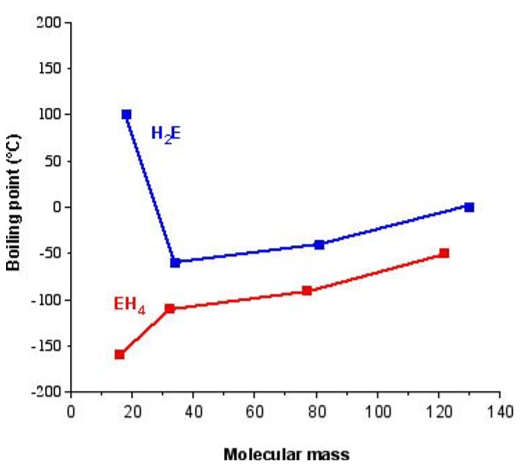
The archetypal case for the effect of hydrogen bonding is the melting and boiling points of the hydrides of the Group 16 elements, i.e., H2E. For a series of analogous compounds with the same molecular structure it would be expected that the boiling points would be related to the molecular mass. However, as can be seen from Table \(\PageIndex{2}\).6, the melting and boiling points of water are anomalously higher than those of its heavier analogs. In fact from Figure \(\PageIndex{2}\).23 it is clear that just considering H2S, H2Se, and H2Te, the expected trend is observed, and it is similar to that for the Group 14 hydrides (CH4, SiH4, etc). Therefore, water must have additional intermolecular forces as compared to its heavier homologs. This observation is consistent with the strong hydrogen bonding in water, and the very weak if nonexistent hydrogen bonding in the sulfur, selenium, and tellurium analogs.
| Compound | Molecular weight (g/mol) | Melting point (◦C) | Boiling Point (◦C) |
|---|---|---|---|
| H2O | 18.01 | 0 | 100 |
| H2S | 24.08 | -85.5 | -60.7 |
| H2Se | 80.98 | -60.4 | -41.5 |
| H2Te | 129.62 | -49 | -2 |
A similar but not as pronounced trend is observed for the Group 15 hydrides, where ammonia's higher values are associated with the presence of significant hydrogen bonding (Table \(\PageIndex{2}\).7).
| Compound | Molecular weight (g/mol) | Melting point (◦C) | Boiling Point (◦C) |
| NH3 | 17.03 | -77.7 | -33.35 |
| PH3 | 34.00 | -133.5 | -87.4 |
| AsH3 | 77.95 | -113.5 | -55 |
| ShH3 | 124.77 | -88.5 | -17 |
Exercise \(\PageIndex{1}\)
Would you expect H2S2 to have a higher or lower boiling point that H2O2? Why?
- Answer
-
The boiling point for H2O2 is 150.2 ◦C, while that of 70.7 ◦C. The difference in boiling point is due to the stronger intermolecular hydrogen bonding in H2O2 than in H2S2.
The types of hydrogen bond can also have a signicant effect on the physical properties of a compound. For example, the cis isomer of hydroxybenzaldehyde melts at 1 ◦C, while the trans isomer has melting and boiling points of 112 ◦C. Both compounds exhibit strong hydrogen bonding in the solid state, however, as may be seen from Figure \(\PageIndex{2}\).24a, cis-hydroxybenzaldehyde (salicylaldehyde) has a configuration that allows strong intramolecular hydrogen bonding, which precludes any intermolecular hydrogen bonding. The melting point of cis-hydroxybenzaldehyde is going to be controlled by the van der Waal forces between adjacent molecules. In contrast, since intramolecular hydrogen bonding is precluded in the trans isomer (Figure \(\PageIndex{2}\).24b) it can form strong intermolecular hydrogen bonds in the solid state, and thus, it is these that define the melting point. The boiling points are controlled in a similar manner.
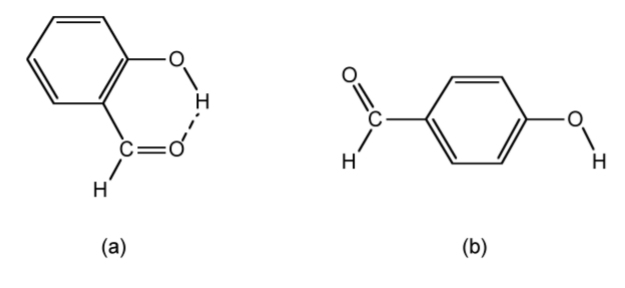
Exercise \(\PageIndex{2}\)
4-Hydroxybenzoic acid melts at 213 ◦C, while 2-hydroxybenzoic acid melts at 158 ◦C. Explain this observation.
- Answer
-
2-Hydroxybenzoic acid exhibits strong intramolecular hydrogen bonding while 4-hydroxybenzoic acid has strong intermolecular hydrogen bonding.
Melting and boiling are not the only physical properties that are aected by hydrogen bonding. Solubility can also be aected. Consider two isomers of C4H10O: nBuOH and Et2O. The n-butanol is much more soluble in water than diethyl ether. The reason for this is that while both compounds can hydrogen bond to water, those between nBuOH and water are much stronger than those between Et2O and water, and thus, dissolution of nBuOH in water does not disrupt the very strong hydrogen bonding in water as much as Et2O does.
Acid strength
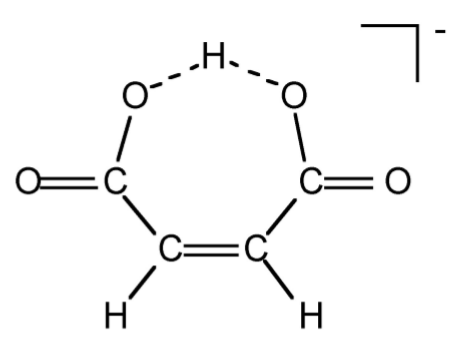
The acidity of a protic species can be affected by the presence of hydrogen bonding. For example, consider the di-carboxylic acid derivatives of ethylene (fumaric acid). Each of the carboxylic acid groups has sequential equilibria that may be defined by the pK values, (2.36). Table \(\PageIndex{2}\).8 lists the pK values for the cis and trans isomers. The acidity of the first and second carboxylic group for the trans isomer is similar, the difference being due to the increased charge on the molecule. In contrast, the second proton in the cis isomer is much less acidic than the first proton: why? A consideration of the structure of the mono anion of the cis isomer (Figure \(\PageIndex{2}\).25) shows that a very strong intramolecular hydrogen bond is formed once the first proton is removed. This hydrogen bond makes the second acidic proton much more difficult to remove and thus lowers the acidity of the proton.
\[ HO_2C-HC=CH-CO_2H \xleftrightarrow{pK_1} O_2^-C-HC=CH-CO_2H \xleftrightarrow{pK_2} O_2^-C-HC=CH-CO_2^- \]
| Isomer | pK1 | pK2 | Ratio |
|---|---|---|---|
| Trans | 3 | 4.5 | 25:1 |
| Cis | 1.9 | 6.2 |
10,000:1 |
Solid state structure
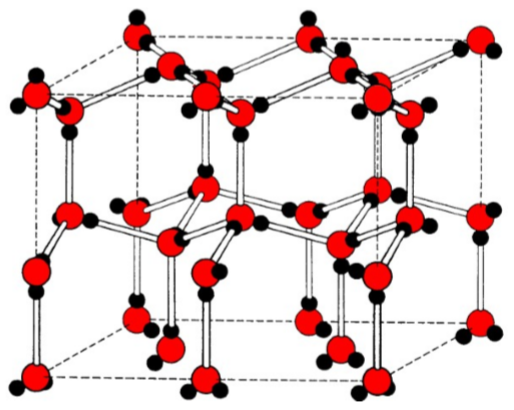
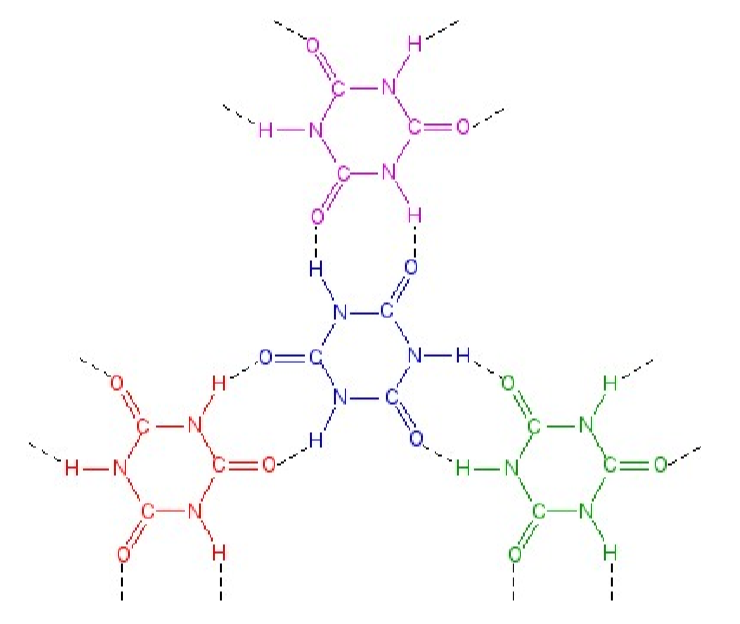
In the solid state, molecules that can form hydrogen bonds will tend to arrange themselves so as to maximize the formation of linear hydrogen bonds. The structure of ice is a typical example, where each water molecule's hydrogen bonds to four other molecules creating a diamond-like lattice (Figure \(\PageIndex{2}\).26). However, ice isn't the only compound whose solid state structure is defined by its hydrogen bonding. Cyanuric acid forms six strong intermolecular hydrogen bonds to three other molecules in the plane of the heterocyclic ring and thus creates a graphite-like structure (Figure \(\PageIndex{2}\).27).
Conformational stabilization
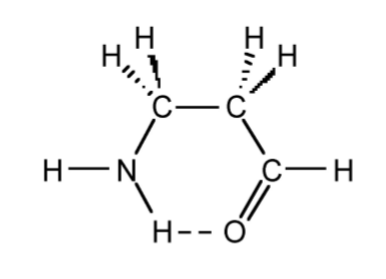
The presence of hydrogen bonding can stabilize certain conformations over others that in the absence of hydrogen bonding would be more favored. For example, based on steric considerations H2NCH2CH2C(O)H would be expected to adopt a staggered conformation as is typical for compounds with free rotation about a C-C bond. However, due to the presence of a strong intramolecular hydrogen bond it adopts a sterically disfavored eclipsed conformation (Figure \(\PageIndex{2}\).28).
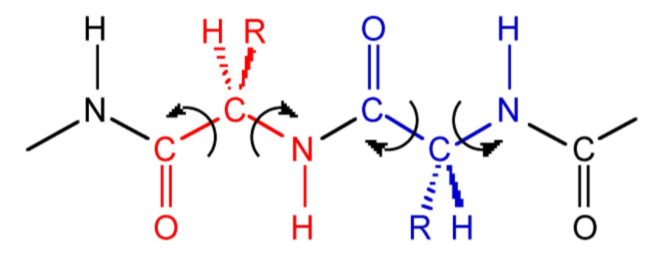
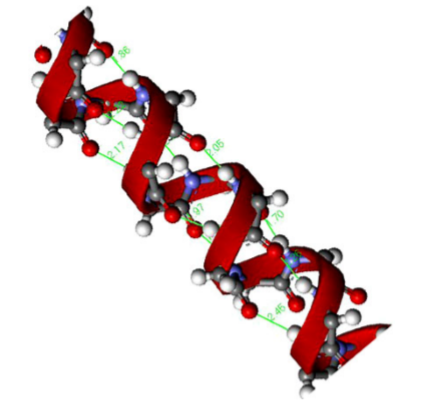
This conformational stabilization is even more important in biopolymers such as peptides. If we assume that a peptide chain (Figure \(\PageIndex{2}\).29) made from a sequence of amino acids would not adopt any eclipsed conformations on steric grounds, and that the amide group (H-N-C=O) is near planar due to delocalization, then there will be 32 possible conformations per nitrogen in the peptide chain, i.e., three each for the C-C and C-N bonds (Figure \(\PageIndex{2}\).29). Assuming a modest peptide has 50 amino acids, there will be 32x50 potential conformations of the polymer chain, i.e., over 5 x 1047 conformations. However, in reality there are limits to the number of conformations observed since particular ones are stabilized by intramolecular hydrogen bonds. The most important of these are the α-helix (Figure \(\PageIndex{2}\).30) and β-sheet structures.
Bibliography
J. T. Leman, J. Braddock-Wilking, A. J. Coolong, and A. R. Barron, Inorg. Chem., 1993, 32, 4324.
K. Nakamoto, M. Margoshes, and R. E. Rundle, J. Am. Chem. Soc., 1955, 77, 6480.
M. B. Power, A. R. Barron, S. G. Bott, E. J. Bishop, K. D. Tierce and J. L. Atwood, J. Chem. Soc., Dalton Trans., 1991, 241.
R. Taylor and O. Kennard, Acc. Chem. Res., 1984, 17, 320.


