1.5: Structure and Bonding - Valence Shell Electron Pair Repulsion (VSEPR) Theory

The idea of a correlation between molecular geometry and the number of valence electrons was first presented in 1940 by Sidgwick and Powell; however, in 1957, Ronald Gillespie (Figure \(\PageIndex{1}\).7) and Sir Ronald Nyholm (Figure \(\PageIndex{1}\).8) refined this concept to build a more detailed theory. It is their work that provides the basis of the valence shell electron pair repulsion (VSEPR) theory, and as such it is also known as the Gillespie-Nyholm theory.

Figure \(\PageIndex{7}\): Chemist Ronald J. Gillespie (1924 -).

Figure \(\PageIndex{8}\): Australian chemist Sir Ronald Sydney Nyholm (1917 -).

One attribute of VSEPR is that with the ability to predict the shape of a molecule for a compound comes the ability to predict some of the physical and chemical properties of that compound.

The formal definition that is the basis for VSEPR is as follows: Pairs of electrons in the valence shell of a central atom of a molecule repel each other and take up positions as far apart as possible.

Within this definition it is implicitly assumed that the core shells are not polarized and therefore take no part in bonding, and therefore can be ignored. Since the maximum repulsion of the electron pairs (be they associated with a bonding interaction or a lone pair) control the shape of a molecule, for each number of electron pairs we can dene the geometric optimum position that maximizes the distance between the electron pairs (Table \(\PageIndex{1}\).6). The number of electron pairs surrounding an atom, both bonding and nonbonding, is called its steric number.

Table \(\PageIndex{1}\).6: Shapes of molecules and ions

Number of central atom electron pairs	Bonding pairs	Non-bonding pairs	Shape	Example
2	2	0	Linear	BeCl2
3	3	0	Triangular	BF3
3	2	1	Bent	SnCl2
4	4	0	Tetrahedral	CCl4
4	3	1	Pyramidal	NH3
4	2	2	Bent	H2O
5	5	0	Trigonal bipyramidal (tbp)	PF5
5	4	1	Pseudo-tdp	BrF4^-
5	3	2	T-Shaped	BrF3
5	2	3	Linear	XeF2
6	6	0	Octahedral	SF6,PF6^-
6	5	1	Square pyramidal	IF5
6	4	2	Square planar	XeF4,IF4^-

The steps for dening the molecular shape are as follows:

1. Draw a simple Lewis structure including single, double, and triple bonds where appropriate.
2. Count the number of electrons on the central atom assuming it is neutral.
3. Add one electron for each σ-bond.
4. Subtract one electron for each π-bond.
5. Subtract one electron for each positive (+) charge.
6. Add one electron for each negative (-) charge.
7. Divide the number of electrons by two to give the number of electron pairs.
8. Use the list in Table \(\PageIndex{1}\).6 to predict the structure of the molecule.

Example \(\PageIndex{1}\)

What is the shape of NH₄⁺

Solution

1. Nitrogen has 5 valence electrons
2. Add 4 electrons for the four σ-bonds: 5 + 4 = 9
3. Subtract one electron for the positive (+) charge: 9 1 = 8
4. Divide the number of electrons by two to give the number of electron pairs: 8/2 = 4
5. Four bonding pairs and no lone pairs = tetrahedral geometry

Exercises

Exercise \(\PageIndex{1}\)

What is the shape of HgCl₂?

Answer

1. Mercury has 2 valence electrons
2. Add 2 electrons for the two σ-bonds: 2 + 2 = 4
3. Divide the number of electrons by two to give the number of electron pairs: 4/2 = 2
4. Two bonding pairs and no lone pairs = linear geometry

Exercise \(\PageIndex{2}\)

What is the shape of H₂CO?

Answer

1. Carbon has 4 valence electrons
2. Add 3 electrons for the three σ-bonds: 4 + 3 = 7
3. Subtract one electron for each π-bond: 7 1 = 6
4. Divide the number of electrons by two to give the number of electron pairs: 6/2 = 3
5. Two bonding pairs and no lone pairs = triangular geometry

Lone pairs versus bonding pairs

The prediction of the detailed molecular structure (including bond angles) is not as simple as shown in Table \(\PageIndex{1}\).6. In molecules with either lone pair electrons or multiple (double or triple) bonds the angles about the central atom are distorted due to the increased electron repulsion (Figure \(\PageIndex{1}\).9). The differences in repulsion caused by a lone pair or a bonding pair may be rationalized in a simple manner by a lone pair taking up more space than a bonding pair (Figure \(\PageIndex{1}\).10).

Figure \(\PageIndex{9}\): The order of decreasing repulsion between non-bonding (unshared) and bonding electron pairs.

Figure \(\PageIndex{10}\): Representation of the relative space taken up by (a) a lone pair of electrons and (b) a bonding pair of electrons.

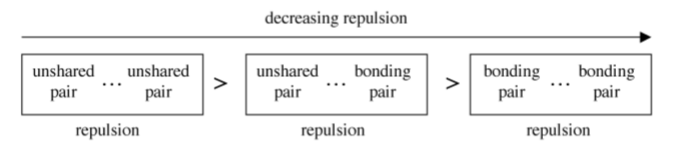
Water is one of the classic cases in considering the issue of non-bonding (unshared) electron pairs.

1. Oxygen has 6 valence electrons
2. Add 2 electrons for the two σ-bonds: 6 + 2 = 8
3. Divide the number of electrons by two to give the number of electron pairs: 8/2 = 4
4. Two bonding pairs and two lone pairs = tetrahedral geometry

From this an idealized tetrahedral geometry would give the H-O-H angle as 109.5^◦, however, from Figure \(\PageIndex{1}\).9 we know that the lone pair...lone pair repulsion is greater than the lone pair...bonding pair repulsion which is greater than the bonding pair...bonding pair repulsion, and thus, the H-O-H angle should be decreased from the ideal tetrahedral. The experimentally determined H-O-H angle in water is in fact 104.5^◦.

Ethylene is a good case in considering the issue of multiple bonds. Ethylene contains both σ-bond and π-bond between the carbon atoms. This combination can be thought of as a super bond, and as such its effect is similar to a lone pair.

Carbon has 4 valence electrons

Add 3 electrons for the two σ-bonds: 4 + 3 = 7

Subtract one electron for each π-bond: 7 1 = 6

Divide the number of electrons by two to give the number of electron pairs: 6/2 = 3

Three bonding pairs and no lone pairs = triangular geometry

From this an idealized tetrahedral geometry would give the H-C-H angle as 120^◦, however, the π-bond repulsion is greater than the σ-bond repulsion, and thus, the H-C-H angle should be decreased from the ideal tetrahedral. The experimentally determined H-O-H angle in water is in fact 118.3^◦.

Resonance structures

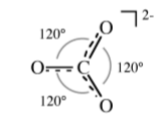
If a molecule or ion has two or more resonance forms it is necessary to consider each form before angles are predicted. For example, the carbonate anion, CO₃^-, can be drawn as a single structure from which it would be predicted that two groups of O-C-O angles would result (Figure \(\PageIndex{1}\).11).

Figure \(\PageIndex{11}\): VSEPR predicted structure of a single resonance form of CO₃^2-.

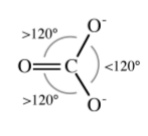
However, CO₃^- should actually be drawn in each of its resonance forms as in Figure \(\PageIndex{1}\).12.

Figure \(\PageIndex{12}\): Resonance forms of CO₃^2-.

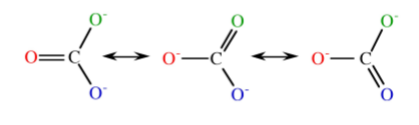
From Figure \(\PageIndex{1}\).12 it is clear that the real structure will be an average of the three resonance forms, and hence there will be a single O-C-O angle = 120^◦ (Figure \(\PageIndex{1}\).13).

Figure \(\PageIndex{13}\): Structure of CO₃^2-.

Atom electronegativities

In an A-X bond where the atom electronegativities are very different the bonding pair is assumed to occupy less space than in bond between two atoms of similar electronegativities. As the bonding pair occupies less space it will repel neighboring electron pairs less.

For example, based on the above, a comparison of the tetrahedral compounds H₂O and F₂O would suggest that the F-O-F angle be smaller than the H-O-H angle since fluorine has a higher electronegativity than hydrogen (4.0 and 2.1, respectively). This is indeed observed (Figure \(\PageIndex{1}\).14).

Figure \(\PageIndex{14}\): Structures of H₂O and F₂O.

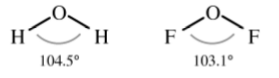
In many cases, inter-ligand steric interactions can also be used to explain the dffierence in angle. For example, while fluorine is more electronegative than chlorine (4.0 versus 3.0, respectively) it is also significantly smaller (Table \(\PageIndex{1}\).7). Thus, a larger Cl-X-Cl angle than a F-X-F angle in the homologous compound, can be attributed to a greater steric interactions, rather than difference in electronegativities.

Table \(\PageIndex{1}\).7: Comparison of size between fluoride and chloride ligands.

Ligand	Covalent Radius (Å)	Van der Waal radius (Å)
F	0.57	1.35
Cl	1.02	1.80

Bent's rule

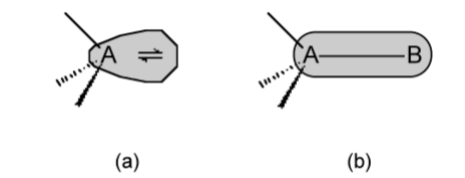
There is the potential for more than one isomer for molecules that adopt structures in which there is a symmetry difference between at least two of the ligand positions. For example a trigional bipyramidal compound of the formula PXY₄ has two possible structures. One where the X occupies an axial position (Figure \(\PageIndex{1}\).15a) and the other where it occupies an equatorial position (Figure \(\PageIndex{1}\).15b).

Figure \(\PageIndex{15}\): The two possible structures of PXY₄.

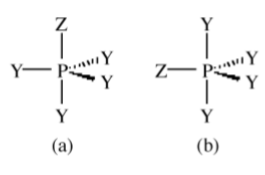
Through the consideration of structures Henry Bent suggested a rule: More electronegative substituents prefer hybrid orbitals with less s character, and conversely, more electropositive substituents prefer hybrid orbitals with greater s character.

For example, in PFCl₅ the fluorine is the most electronegative substituent and will therefore occupy the axial (p-character only) position.

Bibliography

• H. A. Bent, J. Chem. Educ._, 1960, 37, 616.
• H. A. Bent, Chem. Rev., 1961, 61, 275.
• R. J. Gillespie, J. Chem. Educ., 1970, 47, 18.
• R. J. Gillespie, Chem. Soc. Rev., 1992, 21, 59.
• R. J. Gillespie and R. S. Nyholm, Quart. Rev., 1957, 11, 339.