9.9: Resonance Energy of Metals
- Page ID
- 189353
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The solution to the problem above must consider the quantum mechanical nature of the electron. The valence electrons in Na metal are in orbitals that are delocalized over the entire crystal. However in the Na+ e- "salt" form, the electrons are localized on specific anion sites. This localization imparts an additional kinetic energy (via the "particle in a box" effect) that adds to the total energy. From the quantum mechanical result for a particle in a one-dimensional box, we obtain
\[KE= \frac{h^{2}n^{2}}{8mL^{2}}\]
where:
- h = Plank's constant = 6.626 x 10-34 J s
- n = energy level, assumed to be the lowest, n = 1
- m = electron mass = 9.109 x 10-31 kg
- L = size of the box
If we approximate the size of the electron "box" as 3 Å (3 x 10-10 m), we obtain:
\[KE= \frac{(6.626 \cdot 10^{-34})^{2}(6.022 \cdot 10^{23})}{8 \cdot (9.1 \cdot 10^{-31})(3 \cdot 10^{-10})^{2}} = 4.04 \cdot 10^{5} \frac{J}{mol} = + 404 \frac{kJ}{mol}\]
This extra kinetic energy makes the Na+e- "salt" unstable relative to the electron-delocalized metal.
|
Sodium owes its metallic properties to the resonance stabilization of its delocalized valence electrons. |
The calculation is not very accurate because the electron kinetic energy is not zero in the metal, and because the "box" size is not so well defined. However, it does illustrate that electron delocalization has a substantial effect in thermodynamically stabilizing metals. The situation is entirely analogous to the stabilization of aromatic molecules by electron delocalization. In molecules like benzene, resonance is also a quantum-mechanical kinetic energy effect. In general, the resonance stabilization energy is significantly larger in metals than it is in π-delocalized organic molecules. For example, the resonance energy of the six π-electrons in benzene is approximately 151 kJ/mol, less than half of the value we have calculated (per electron) in sodium metal.
Interestingly, several of the alkali metals (and other metallic elements) transform at ultrahigh pressures to optically transparent, insulating phases in which the valence electrons are localized.[10][11] These high pressure electride phases defy the general rule (which we will encounter in Chapter 10) that insulators transform to metals at sufficiently high density. They illustrate how the stable structure of an element can depend on the trade-off between the lattice energy of an ionic electride structure and the resonance energy of an electron-delocalized metal.
|
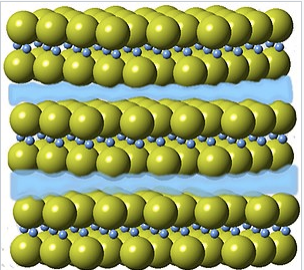
Crystal structure of Ca2N, with 2D electron layers shown schematically in blue. |
In addition to the salt-like electrides that are formed by complexing alkali metals with crown ether ligands, there are a number of recently discovered solid state nitrides and oxides, such as Ca2N and Ca24Al28O64, that are more properly formulated as electrides, i.e. as [Ca2N+](e-)[12] and [Ca24Al28O64]4+(e−)4.[13] In these compounds the Ca, Al, O, and N atoms have their ordinary octet oxidation states (+2, +3, -2, and -3, respectively), and electrons act as anions, filling in cage-like voids or layers in the crystal. For example, Ca2N adopts the anti-CdCl2 structure, as shown at the right, with void spaces between layers that are occupied by a 2D gas of electrons. Like other layered materials, Ca2N can be easily delaminated into thin nanosheets while retaining its structure and properties as an electride.[14] These compounds are powerful reducing agents and also have interesting activity as catalysts.[15]