9.3: Energetics of Crystalline Solids- The Ionic Model
- Page ID
- 183348
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Many ionic compounds have simple structures. Because the forces holding the atoms together are primarily electrostatic, we can calculate the cohesive energy of the crystal lattice with good accuracy. Interesting questions to ask about these lattice energy calculations are:
- How accurate are lattice energy calculations?
- What do they teach us about the chemical bonds in ionic crystals?
- Can we use lattice energies to predict properties such as solubility, stability, and reactivity?
- Can we use lattice energies to predict the crystal structures of ionic compounds?
Let's start by looking at the forces that hold ionic lattices together. There are mainly two kinds of force that determine the energy of an ionic bond.
|
The NaCl crystal structure is the archetype for calculating lattice energies and computing enthalpies of formation from Born-Haber cycles. |
1) Electrostatic Force of attraction and repulsion (Coulomb's Law): Two ions with charges z+ and z-, separated by a distance r, experience a force F:
\[\mathbf{F} = -\frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r^{2}}\]
where
e = 1.6022×10−19 C
4 π ε0 = 1.112×10−10 C²/(J m)
This force is attractive for ions of opposite charge.
The electrostatic potential energy, Eelec, is then given by
\[\mathbf{E}_{elec} \int_{\infty}^{r} F(r)dr = \frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r}\]
The sign of Eelec is negative for the attractive interaction between a cation and an anion. That is, the closer oppositely charged ions approach each other, the lower the potential energy.
2) Closed-shell repulsion. When electrons in the closed shells of one ion overlap with those of another ion, there is a repulsive force comes from the Pauli exclusion principle. A third electron cannot enter an orbital that already contains two electrons. This force is short range, and is typically modeled as falling off exponentially or with a high power of the distance r between atoms. For example, in the Born approximation, B is a constant and ρ is a number with units of length, which is usually empirically determined from compressibility data. A typical value of ρ is 0.345 Å.
\[\mathbf{E}_{repulsion} = Bexp(\frac{-r}{\rho})\]
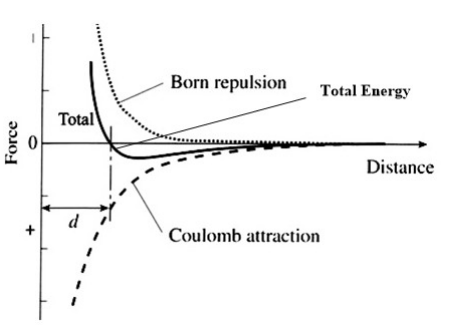
The energy of the ionic bond between two atoms is then calculated as the combination of net electrostatic and the closed-shell repulsion energies, as shown in the figure at the right. Note that for the moment we are ignoring the attractive van der Waals energy between ions, which we will explain below. For a pair of ions, the equilibrium distance between ions is determined by the minimum in the total energy curve. At this distance, the net force on each ion is zero.
Electrostatic energy of a crystal lattice
We can use these equations to calculate the lattice energy of a crystal by summing up the interactions between all pairs of ions. Because the closed-shell repulsion force is short range, this term is typically calculated only for interactions between neighboring ions. However, the Coulomb force is long range, and must be calculated over the entire crystal. This problem was first solved in 1918 by Erwin Madelung, a German physicist.[4]
Consider an ion in the NaCl structure labeled "O" in the diagram at the right. We can see that the nearest neighbor interactions (+ -) with ions labeled "1" are attractive, the next nearest neighbor interactions (- - and + +) are repulsive, and so on. In the NaCl structure, counting from the ion in the center of the unit cell, there are 6 nearest neighbors (on the faces of the cube), 12 next nearest neighbors (on the edges of the cube), 8 in the next shell (at the vertices of the cube), and so on. Their distances from ion "0" increase progressively: ro, √2 ro, √3 ro, and so on, where ro is the nearest neighbor distance.
We can now write the electrostatic energy at ion "O" as:
\[\mathbf{E}_{elec} = -6\frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} + 12 \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{\sqrt{2}r_{o}} -8 \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{\sqrt{3}r_{o}} + \dots \]
Factoring out constants and the nearest-neighbor bond distance ro we obtain:
\[\mathbf{E}_{elec} = \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}}(6 - \frac{12}{\sqrt{2}} + \frac{8}{\sqrt{3}} - \frac{6}{\sqrt{4}} + \dots) \]
Where the sum in parentheses, which is unitless, slowly converges to a value of A = 1.74756. Generalizing this formula for any three-dimensional ionic crystal we get a function:
\[\mathbf{E}_{elec} = \frac{e^{2}}{4 \pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} NA\]
where N is Avogadro's number (because we are calculating energy per mole of ions) and A is called the Madelung constant. The Madelung constant depends only on the geometrical arrangement of the ions and so it varies between different types of crystal structures, but within a given structure type it does not change. Thus MgO and NaCl have the same Madelung constant because they both have the NaCl structure
|
The Madelung constant is calculated by summing up electrostatic interactions with ion labeled 0 in the expanding spheres method. Each number designates the order in which it is summed. For example, ions labeled 1 represent the six nearest neighbors (attractive interaction), ions labeled 2 are the 12 next nearest neighbors (repulsive interaction) and so on. Note that if the sum is carried out over shells 1-2-3..., it converges very slowly, but there are mathematical methods for summing it which give a rapidly converging series. |
The table below lists Madelung constants for some common structures. The reduced Madelung constant is obtained by normalizing the values to the number of ions in the formula unit. It can be seen from the table that the reduced Madelung constants are quite similar for different structures. This makes it hard to determine on the basis of electrostatic energy calculations which structure will be most stable for a given compound. It is interesting to note that the trend in reduced Madelung constants roughly follows the trend in ionicity (cf. the Mooser-Pearson diagram in Section 9.2). For example, wurtzite has a slightly higher Madelung constant than zincblende, consistent with our earlier conclusion that the wurtzite structure is favored by more polar compounds.
| Structure | Madelung Constant, A | Reduced Madelung Constant, 2A/n |
|---|---|---|
| NaCl (halite) | 1.7476 | 1.7476 |
| CsCl | 1.7627 | 1.7627 |
| ZnS (zincblende) | 1.6381 | 1.6381 |
| ZnS (wurtzite) | 1.6413 | 1.6413 |
| CaF2 (fluorite) | 2.5194 | 1.6796 |
| TiO2 (rutile) | 2.4080 | 1.6053 |
| Al2O3 (corundum) | 4.172 | 1.6688 |
Total lattice energy of a crystal
Having in hand a formula for the electrostatic energy, we can now add in the closed-shell repulsion term to obtain an equation that gives us the total lattice energy.
\[E_{L} = \frac{e^{2}}{4\pi \varepsilon_{0}} \frac{z_{+}z_{-}}{r_{o}} NA + NBexp(\frac{-r}{\rho})\]
At the equilibrium bond distance, the forces on all the ions are zero, and we can use this fact to eliminate the constant B:
\[[\frac{dE}{dr}]_{r=r_{o}} = 0\]
Expressed this way, EL is a negative number (because z+ and z- have opposite signs). It represents the energy change for forming one mole of solid salt from one mole of the gaseous ions, separated initially at an infinite distance.
|
Lithium fluoride (shown here as a large single crystal in a beaker of water) is the only alkali halide that is not freely soluble in water. The lattice energy of LiF is the most negative of the alkali fluorides because Li+ and F- are both small ions and EL is proportional to 1/r0. |





