8.9: Problems
- Page ID
- 189233
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1. For each of the following close packed layer sequences, indicate the name of the structure (structure type), the coordination environment of the cations (represented by lower case letters), and the coordination environment of the anions (upper case letters). Give two additional examples (apart from the structure type itself) of compounds with the same structure.
(a) AbBaAbBaAbB......
(b) AaBbCcAaBbCc.....
(c) AcBaCbAcBaCb.....
(d) AcB | AcB | AcB |.... ("|" = van der Waals gap)
2. Below are sections of the lithium oxide unit cell.
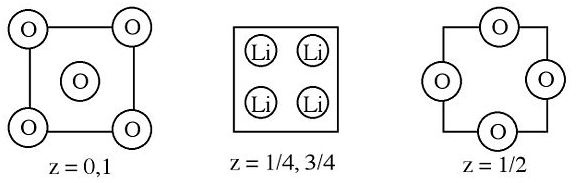
(a) Describe how to obtain (and do obtain) the empirical formula.
(b) What is the coordination number and geometry for each type of ion?
(c) Which atom is close-packed?
(d) What type and fraction of holes are filled by the other ion?
3. The hexagonal unit cell of a metal nitride is shown below in sections.
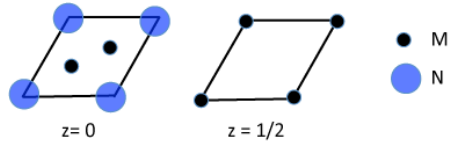
(a) What is the empirical formula of the compound?
(b) How many M atoms are coordinated to each N atom?
(c) In what group of the periodic table would you expect to find M?
4. Draw the cubic Li3Bi unit cell in sections.
5. If half the cesium is removed from the CsCl structure, such that each Cl atom is then tetrahedrally coordinated, what structure type is generated?
6. The crystal structure of barium titanate is shown below.
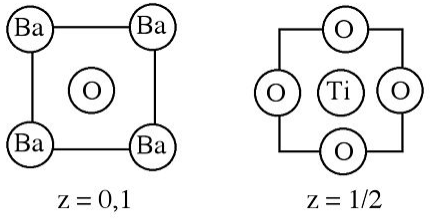
(a) What is the empirical formula of the compound?
(b) Which atoms (if any) are close packed?
(c) How many oxygen atoms coordinate (i) Ti4+ and (ii) Ba2+?
(d) Why are the coordination numbers are different?
7. The structures of the disulfides (MS2) show an apparently unusual trend, proceeding from left to right across the transition series. On the left side (TiS2, ZrS2, MoS2, etc.), one finds layered structures, whereas in the middle (ReS2, FeS2, RuS2) there are three-dimensional pyrite- and marcasite-type structures. On the right (PtS2, SnS2), there are again layered structures. Briefly explain these trends.
8. Explain why ionic compounds rarely have layered crystal structures.
9. Draw the zincblende structure in sections.
10. The zincblende structure is rarely found with very polar or ionic compounds. However, some polar and ionic compounds (BeO, NH4F, etc.) have the wurtzite structure.
(a) Describe the similarities and the differences between the zincblende and wurtzite structures (in terms of coordination numbers, stacking sequence of cations and anions, etc.) (b) Why is wurtzite more ionic than zincblende?
11. A recent article by R. Cava and co-workers (Nature Materials 2010, 9, 546-9) describes the unusual electronic properties of a Y-Pt-Bi alloy, the structure of which is shown in sections below:
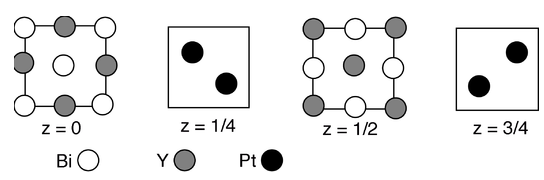
(a) What is the stoichiometry of the compound?
(b) How many Y and how many Pt atoms coordinate each Bi atom?
12. The fluorite structure, CaF2, which is generated by filling all the tetrahedral holes in a FCC array, is a common MX2 structure type.
(a) What is the coordination environment of F in a hypothetical relative of CaF2, in which Ca forms a hcp array and F occupies all the tetrahedral sites?
(b) Suggest a reason why the structure described in (a) is very rare.
13. The cuprite (Cu2O) structure is related to zincblende (or diamond) in that oxygen occupies both the Zn and S positions, with copper in between. This is shown schematically at the right. Actually, in cuprite there are two such interpenetrating networks with no bonds between them. Draw the second network in the empty cell. If you put the two halves together and take out the copper, what cubic packing lattice do you get? Is it a closest packing lattice? (Hint #1: start with an O atom at 1/2,1/2,1/2) (Hint #2: try this in pencil first)

14. Draw the rutile structure in sections of the unit cell, and verify that the stoichiometry is MX2. What are the coordination numbers of Ti and O?
15. Stishovite is a high pressure form of SiO2 found in meteorite craters. While normal SiO2 has the quartz structure, in which each Si is coordinated by four O atoms, stishovite has the rutile structure. Would you expect the Si-O bond to be longer in stishovite, or in quartz? What is the bond order in each polymorph?
16. Na and Cl combine in a 1:1 ratio to make the ionic NaCl lattice. Interestingly, recent theoretical predictions (confirmed by high pressure synthesis and crystallography) have identified several other stoichiometries that form stable crystals at high pressure. These include Na3Cl, Na2Cl, Na3Cl2, NaCl3, and several others.[8] The structure of one of these new sodium chlorides is shown below in sections.
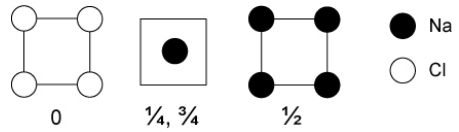
a) What is the stoichiometry of this compound?
b) What are the coordination numbers of Na and Cl, and how do they compare to the coordination numbers in NaCl and Na metal?
c) Based on your answer to (b), explain why high pressure should stabilize this phase.
17. One of the new compounds discovered in the study described in problem 16 is NaCl3. There are two polymorphs of this compound, one of which contains linear Cl3- ions. Accurate molecular orbital calculations indicate that the charge on the central Cl atom in these linear anions is close to zero. Draw a valence bond structure for the Cl3- ion that is consistent with these observations. Would you expect the Cl-Cl bond to be longer or shorter than the bond in Cl2?
18. Some MX salts can exist in either the CsCl or NaCl structure. Use the Pauling formula to predict the M-X bond length in the CsCl structure of a compound that has a bond length of 3.5 Å in the NaCl structure. Would applying a high pressure stabilize the CsCl form, or the NaCl form of this compound? (hint: calculate the volume per formula unit)
19. Mn3O4 and Fe3O4 are both mixed-valence oxides. In both cases, there is one M2+ ion and two M3+ ions per formula unit (M = Fe, Mn).
- (a) One of these is a normal spinel and one is an inverse spinel. Explain which is which, and why. (hint: think about CFSE's)
- (b) For Mn3O4, what kind of magnetic ordering (ferri-, ferro-, or antiferromagnetic) would you expect, and why? You can assume that neighboring tetrahedral and octahedral ions in the structure are antiferromagnetically coupled.
- (c) Sketch the approximate form of the χ vs. T and 1/χ vs. T curves for Mn3O4. Label any special values of temperature on your graphs.
20. Predict whether each of the following should form a normal or inverse spinel: MgV2O4, VMg2O4, NiGa2O4, ZnCr2S4, NiFe2O4. Would kind of magnetic ordering (ferro-, ferri-, or antiferromagnetic) would you predict for NiFe2O4?


