6.6: Conduction in Metals
- Page ID
- 183329
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In metals, the valence electrons are in molecular orbitals that extend over the entire crystal lattice. As we will learn in Chapter 7, metals are almost always crystalline and the individual crystal grains are typically micron size. This means that the spatial extent of the orbitals is very large compared to the size of the atoms or the unit cell. The diagram at the left shows a generic plot of electron energy vs. density of states for a metal such as Na, Cu, or Ag. In these cases, there are N orbitals for N electrons, and each orbital can accommodate two electrons. Therefore the Fermi level, which corresponds to the energy of the highest occupied MO at zero temperature, is somewhere in the middle of the band of orbitals. The energy level spacing between orbitals is very small compared to the thermal energy kT, so we can think of the orbitals as forming a continuous band.
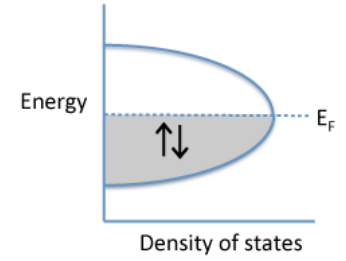
Classically, if the electrons in this band were free to be thermally excited, we would expect them to have a specific heat of 3R per mole of electrons. However, experimentally we observe that Cp is only about 0.02 R per mole. This suggests that only about 1% of the electrons in the metal can be thermally excited at room temperature. However, essentially all of the valence electrons are free to move in the crystal and contribute to electrical conduction. To understand this apparent paradox, we need to recall that the electrons exist in quantized energy levels.
Because of quantization, electrons in metals have a Fermi-Dirac distribution of energies. In this distribution, most of the electrons are spin-paired, although the individual electrons in these pairs can be quite far apart since the orbitals extend over the entire crystal. A relatively small number of electrons at the top of the Fermi sea are unpaired by thermal excitation. This is the origin of the Pauli paramagnetism of metals.
How fast are electrons traveling in a typical metal? Because of the bell shape of the E vs. DOS curve, most of the electrons have E ≈ EF. At the midpoint energy (EF) of the band, the MO's have one node for every two atoms. We can calculate the de Broglie wavelength as twice the distance between nodes and thus:
λ = 4a at the midpoint of the band.
where a is the interatomic spacing. Since a typical value of a is about 2 Å, we obtain the de Broglie wavelength λ ≈ 8 Å.
Using the de Broglie relation p = h/λ, we can write:
\[\mathbf{p = \frac{h}{\lambda} = m_{e}v_{F}}\]
where me is the mass of the electron and vF is the velocity of electrons with energy EF.
Solving for \(V_{F} = \frac{h}{m_{e}\lambda}\)we obtain \(\mathbf{v_{F}} = \frac{(6.62 \times 10^{-34} J s)}{(9.1 \times 10^{-31} kg)(8 \times 10^{-10}m)} = \mathbf{1.0 \times 10^{6} m/s}\)
Experimental values of vF are 1.07 x 106 and 1.39 x 106 m/s for Na and Ag, respectively, so our approximations are pretty good.
How fast are electrons moving in metals? Really, really fast!! 1,000,000 meters per second! This is about 1/300 the speed of light, and about 3000 times the speed of sound in air (3 x 102 m/s).
However, the drift velocity of electrons in metals - the speed at which electrons move in applied electric field - is quite slow, on the order of 0.0001 m/s, or .01 cm/s. You can easily outrun an electron drifting in a metal, even if you have been drinking all night and have been personally reduced to a very slow crawl.
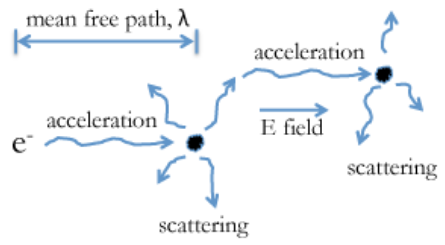
In order to understand the great disparity between the Fermi velocity and the drift velocity of electrons in metals, we need to consider a picture for the scattering of electrons, and their acceleration in an electric field, as shown at the left. If we apply a voltage across a metal (e.g., a metal wire), the electrons are subjected to an electric field E, which is the voltage divided by the length of the wire. This electric field exerts a force on the electron, causing it to accelerate. However, the electron is frequently scattered, mostly by phonons (lattice vibrations). Each time the electron is scattered its acceleration starts all over again. The time between scattering events is τ and the distance the electrons travel between scattering events is the mean free path, λ. (Note that this is NOT the same λ as the de Broglie wavelength, they just unfortunately have the same symbol!)
We can write the force on the electron as:
\[\mathbf{F = eE = m_{e}a = \frac{m_{e}v_{drift}}{\tau}}\]
In this equation, a is the acceleration in the electric field, me is the mass, and vdrift is the drift velocity of the electron.
Experimentally, the mean free path is typically obtained by measuring the scattering time. For an electron in Cu metal at 300 K, the scattering time τ is about 2 x 10-14 s. From this we can calculate the mean free path as:
\[\mathbf{\lambda = v_{avg}\tau \approx v_{F}\tau} = (1 \times 10^{6} m/s)(2 \times 10^{-14}) = \mathbf{40 nm}\]
The mean free path (40 nm = 400 Å) is quite long compared to the interatomic spacing (2 Å). To put it in perspective, if the interatomic spacing were scaled to the length of a football (0.3 m), the mean free path would be over half the length of the football field (60 m). Thus an electron travels a fairly long way between scattering events and scarcely notices the atomic structure of the metal in which it is traveling.
To summarize, electrons are traveling in metals at the Fermi velocity vF, which is very, very fast (106 m/s), but the flux of electrons is the same in all directions. That is, they are going nowhere fast. In an electric field, a very small but directional drift velocity is superimposed on this fast random motion of valence electrons.
|
For ordinary metals, the mean free path of a valence electron (λ) is quite long relative to the interatomic spacing, represented in this analogy as the length of a football. |
We can calculate the drift velocity of electrons as the acceleration in the electric field times the scattering time:
From F = ma, we obtain the acceleration (a) as:
\[\mathbf{a = \frac{F}{m_{e}} = \frac{eE}{m_{e}}}\]
And thus,
\[\mathbf{v_{drift} = a\tau = \frac{eE\tau}{m_{e}}}\]
If we divide both sides of this equation by the magnitude of the electric field (E), we obtain the mobility (μ):
\[\mathbf{\mu=\frac{v_{drift}}{E}= \frac{e\tau}{m_{e}}}\]
μ has units of velocity/field = cm/s / V/cm = cm2/Vs
An important consequence of the calculation of vdrift is Ohm's Law, V = iR. From the equations above, we can see that the drift velocity increases linearly with the applied electric field. The drift velocity (cm/s) is proportional to the current (i, coul/s), and the electric field (E, V/cm) is proportional to the voltage (V):
\[\mathbf{Current \: (i) = nev_{drift} \times area}\]
\[\mathbf{Voltage \: (V) = E \times length}\]
Here n is the density of valence electrons (#/cm3) and e is the charge of the electron (coul). Combining these equations with our equation for vdrift we obtain:
\[V = i(\frac{m_{e}}{ne^{2}\tau})\frac({length}{area}) = iR\]
Thus, V = iR, where R is the combination of the two terms in parentheses. The first of these is the resistivity, \(\rho\), and the second is a geometrical factor.
The conductivity (σ) of a metal, which is the inverse of \(\rho\), is proportional to μ, which in turn is proportional to τ (and λ):
\[\mathbf{\sigma = ne\mu = \frac{ne^{2}\tau}{m_{e}}}\]
We can use this equation to work out the conductivity of a specific metal (Cu), for which n = 8.5 x 1022 cm-3 and τ = 2 x 10-14 s. Putting in the numbers for me and e, we obtain σ = 7 x 105 Ω-1 cm-1 for Cu, in good agreement with the measured value (6 x 105 Ω-1cm-1).



