6.4: Crystal Structures of Metals
- Page ID
- 183327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Crystalline Nature of Metals
All metallic elements (except Cs, Ga, and Hg) are crystalline solids at room temperature. Like ionic solids, metals and alloys have a very strong tendency to crystallize, whether they are made by thermal processing or by other techniques such as solution reduction or electroplating. Metals crystallize readily and it is difficult to form a glassy metal even with very rapid cooling. Molten metals have low viscosity, and the identical (essentially spherical) atoms can pack into a crystal very easily. Glassy metals can be made, however, by rapidly cooling alloys, particularly if the constituent atoms have different sizes. The different atoms cannot pack in a simple unit cell, sometimes making crystallization slow enough to form a glass.
|
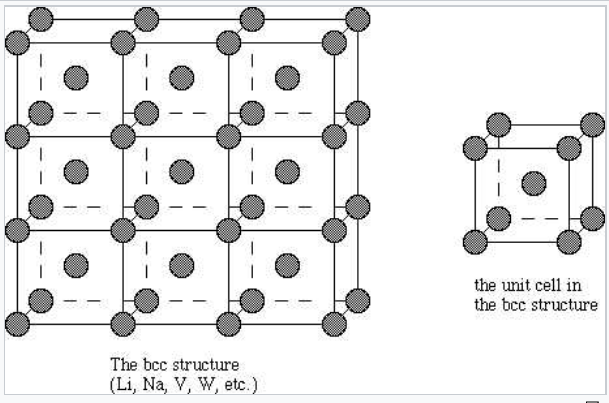
Body-centered cubic |
|
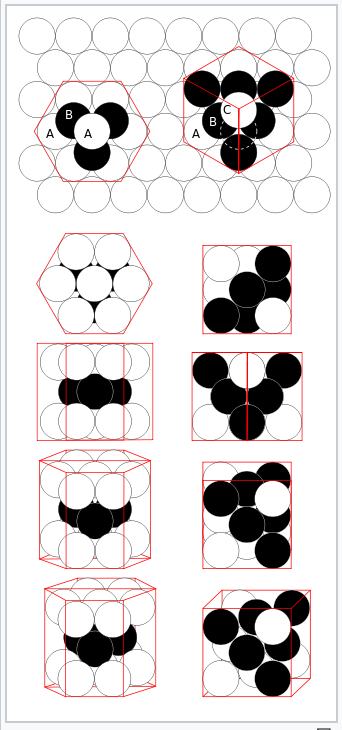
hcp (left) and fcc (right) close-packing of spheres |
Crystal structures
Most metals and alloys crystallize in one of three very common structures: body-centered cubic (bcc), hexagonal close packed (hcp), or cubic close packed (ccp, also called face centered cubic, fcc). In all three structures the coordination number of the metal atoms (i.e., the number of equidistant nearest neighbors) is rather high: 8 for bcc, and 12 for hcp and ccp. We can contrast this with the low coordination numbers (i.e., low valences - like 2 for O, 3 for N, or 4 for C) found in nonmetals. In the bcc structure, the nearest neighbors are at the corners of a cube surrounding the metal atom in the center. In the hcp and ccp structures, the atoms pack like stacked cannonballs or billiard balls, in layers with a six-coordinate arrangement. Each atom also has six more nearest neighbors from layers above and below. The stacking sequence is ABCABC... in the ccp lattice and ABAB... in hcp. In both cases, it can be shown that the spheres fill 74% of the volume of the lattice. This is the highest volume fraction that can be filled with a lattice of equal spheres.
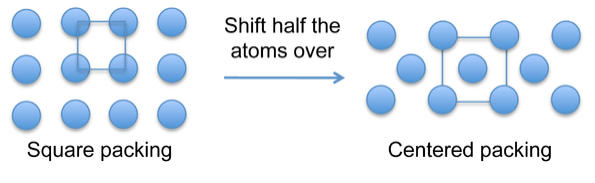
Atoms in metallic crystals have a tendency to pack in dense arrangments that fill space efficiently. The simple square packing (above) upon which the simple cubic structure is based is inefficient and thus rare among metallic crystal structures. Body- or face-centered structures fill space more efficiently and more common.
Periodic trends in structure and metallic behavior
Remember where we find the metallic elements in the periodic table - everywhere except the upper right corner. This means that as we go down a group in the p-block (let's say, group IVA, the carbon group, or group VA, the nitrogen group), the properties of the elements gradually change from nonmetals to metalloids to metals. The carbon group nicely illustrates the transition. Starting at the top, the element carbon has two stable allotropes - graphite and diamond. In each one, the valence of carbon atoms is exactly satisfied by making four electron pair bonds to neighboring atoms. In graphite, each carbon has three nearest neighbors, and so there are two single bonds and one double bond. In diamond, there are four nearest neighbors situated at the vertices of a tetrahedron, and so there is a single bond to each one.
The two elements right under carbon (silicon and germanium) in the periodic table also have the diamond structure (recall that these elements cannot make double bonds to themselves easily, so there is no graphite allotrope for Si or Ge). While diamond is a good insulator, both silicon and germanium are semiconductors (i.e., metalloids). Mechanically, they are hard like diamond. Like carbon, each atom of Si and Ge satisfies its valence of four by making single bonds to four nearest neighbors.
The next element under germanium is tin (Sn). Tin has two allotropes, one with the diamond structure, and one with a slightly distorted bcc structure. The latter has metallic properties (metallic luster, malleability), and conductivity about 109 times higher than Si. Finally, lead (Pb), the element under Sn, has the ccp structure, and also is metallic. Note the trends in coordination number and conducting properties:
| Element | Structure | Coord. no. | Conductivity |
|---|---|---|---|
| C | graphite, diamond | 3, 4 | semimetal, insulator |
| Si | diamond | 4 | semiconductor |
| Ge | diamond | 4 | semiconductor |
| Sn | diamond, distorted bcc | 4, 8 | semiconductor, metal |
| Pb | ccp | 12 | metal |

The elements C, Si, and Ge obey the octet rule, and we can easily identify the electron pair bonds in their structures. Sn and Pb, on the other hand, adopt structures with high coordination numbers. They do not have enough valence electrons to make electron pair bonds to each neighbor (this is a common feature of metals). What happens in this case is that the valence electrons become "smeared out" or delocalized over all the atoms in the crystal. It is best to think of the bonding in metals as a crystalline arrangement of positively charged cores with a "sea" of shared valence electrons gluing the structure together. Because the electrons are not localized in any particular bond between atoms, they can move in an electric field, which is why metals conduct electricity well. Another way to describe the bonding in metals is nondirectional. That is, an atom's nearest neighbors surround it in every direction, rather than in a few particular directions (like at the corners of a tetrahedron, as we found for diamond). Nonmetals (insulators and semiconductors), on the other hand, have directional bonding. Because the bonding is non-directional and coordination numbers are high, it is relatively easy to deform the coordination sphere (i.e., break or stretch bonds) than it is in the case of a nonmetal. This is why elements like Pb are much more malleable than C, Si, or Ge.