5.8: Jahn-Teller Effect
- Page ID
- 188706
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Jahn–Teller effect, sometimes also known as Jahn–Teller distortion, describes the geometrical distortion of molecules and ions that is associated with certain electron configurations. This electronic effect is named after Hermann Arthur Jahn and Edward Teller, who proved, using group theory, that orbitally degenerate molecules cannot be stable.[15] The Jahn–Teller theorem essentially states that any non-linear molecule with a spatially degenerate electronic ground state will undergo a geometrical distortion that removes that degeneracy, because the distortion lowers the overall energy of the molecule.

We can understand this effect in the context of octahedral metal complexes by considering d-electron configurations in which the eg orbital set contains one or three electrons. The most common of these are high spin d4 (e.g., CrF2) , low spin d7 (e.g.,NaNiO2), and d9 (e.g., Cu2+). If the complex can distort to break the symmetry, then one of the (formerly) degenerate eg orbitals will go down in energy and the other will go up. More electrons will occupy the lower orbital than the upper one, resulting in an overall lowering of the electronic energy. A similar distortion can occur in tetrahedral complexes when the t2 orbitals are partially filled. Such geometric distortions that lower the electronic energy are said to be electronically driven. Similar electronically driven distortions occur in one-dimensional chain compounds, where they are called Peierls distortions, and in two-dimensionally bonded sheets, where they are called charge density waves.
The Jahn–Teller effect is most often encountered in octahedral complexes, especially six-coordinate copper(II) complexes.[16] The d9 electronic configuration of this ion gives three electrons in the two degenerate eg orbitals, leading to a doubly degenerate electronic ground state. Such complexes distort along one of the molecular fourfold axes (always labelled the z axis), which has the effect of removing the orbital and electronic degeneracies and lowering the overall energy. The distortion normally takes the form of elongating the bonds to the ligands lying along the z axis, but occasionally occurs as a shortening of these bonds instead (the Jahn–Teller theorem does not predict the direction of the distortion, only the presence of an unstable geometry). When such an elongation occurs, the effect is to lower the electrostatic repulsion between the electron-pair on the Lewis basic ligand and any electrons in orbitals with a z component, thus lowering the energy of the complex. If the undistorted complex would be expected to have an inversion center, this is preserved after the distortion.
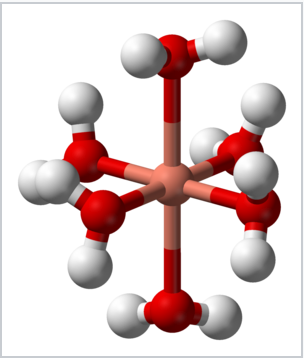
In octahedral complexes, the Jahn–Teller effect is most pronounced when an odd number of electrons occupy the eg orbitals. This situation arises in complexes with the configurations d9, low-spin d7 or high-spin d4 complexes, all of which have doubly degenerate ground states. In such compounds the eg orbitals involved in the degeneracy point directly at the ligands, so distortion can result in a large energetic stabilization. Strictly speaking, the effect also occurs when there is a degeneracy due to the electrons in the t2g orbitals (i.e. configurations such as d1 or d2, both of which are triply degenerate). In such cases, however, the effect is much less noticeable, because there is a much smaller lowering of repulsion on taking ligands further away from the t2g orbitals, which do not point directly at the ligands (see the table below). The same is true in tetrahedral complexes (e.g. manganate: distortion is very subtle because there is less stabilisation to be gained because the ligands are not pointing directly at the orbitals.
The expected effects for octahedral coordination are given in the following table:
| Number of d electrons | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High/Low Spin | HS | LS | HS | LS | HS | LS | HS | LS | ||||||
| Strength of J-T Effect | w | w | s | w | w | w | w | s | s | |||||
w: weak Jahn–Teller effect (t2g orbitals unevenly occupied)
s: strong Jahn–Teller effect expected (eg orbitals unevenly occupied)
blank: no Jahn–Teller effect expected.
The Jahn–Teller effect is manifested in the UV-VIS absorbance spectra of some compounds, where it often causes splitting of bands. It is readily apparent in the structures of many copper(II) complexes.[17] Additional, detailed information about the anisotropy of such complexes and the nature of the ligand binding can be obtained from the fine structure of the low-temperature electron spin resonance spectra.