4.3: Electrochemical Potentials
- Page ID
- 183312
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In electrochemical cells, or in redox reactions that happen in solution, the thermodynamic driving force can be measured as the cell potential. Chemical reactions are spontaneous in the direction of -ΔG, which is also the direction in which the cell potential (defined as Ecathode - Eanode) is positive. A cell operating in the spontaneous direction (for example, a battery that is discharging) is called a galvanic cell. A cell that is being driven in the non-spontaneous direction is called an electrolytic cell. For example, let us consider the reaction of hydrogen and oxygen to make water:
\[\ce{2H2_{(g)} + O2_{(g)} = 2H2O_{(l)}}\]
Thermodynamically, this reaction is spontaneous in the direction shown and has an overall standard free energy change (ΔG°) of -237 kJ per mole of water produced.
When this reaction occurs electrochemically in the spontaneous direction (e.g., in a hydrogen-air fuel cell), the two half cell reactions that occur are:
Anode: \(\ce{H2_{(g)} ->2H^{+}_{(aq)} + 2e^{-}}\)
Cathode: \(\ce{O2_{(g)} + 4H^{+}_{(aq)} + 4e^{-} -> 2H2O_{(l)}}\)
Here the anode is the negative electrode and the cathode is the positive electrode; under conditions of very low current density (where there are minimal resistive losses and kinetic overpotentials), the potential difference we would measure between the two electrodes would be 1.229 V.
In an electrolytic cell, this reaction is run in reverse. That is, we put in electrical energy to split water into hydrogen and oxygen molecules. In this case, the half reactions (and their standard potentials) reverse. O2(g) bubbles form at the anode and H2(g) is formed at the cathode. Now the anode is the positive electrode and the cathode is negative. Electrons are extracted from the substance at the anode (water) and pumped into the solution at the cathode to make hydrogen. An animation of the cathode half reaction is shown below.
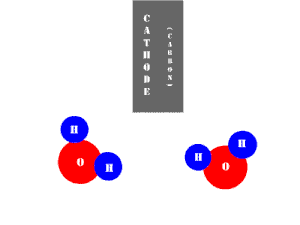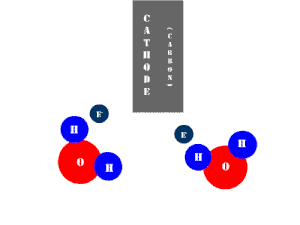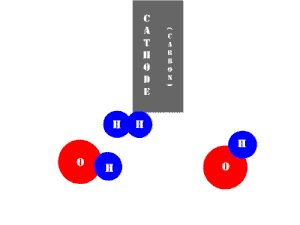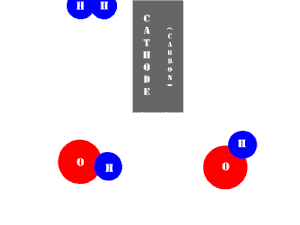
In both galvanic and electrolytic cells, oxidation occurs at the anode and reduction occurs at the cathode.
Half-cell potentials
As noted above, the equilibrium voltage of an electrochemical cell is proportional to the free energy change of the reaction. Because electrochemical reactions can be broken up into two half-reactions, it follows that the potentials of half reactions (like free energies) can be added and subtracted to give an overall value for the reaction. If we take the standard hydrogen electrode as our reference, i.e., if we assign it a value of zero volts, we can measure all the other half cells against it and thus obtain the voltage of each one. This allows us to rank redox couples according to their standard reduction potentials (or more simply their standard potentials), as shown in the table below.

Note that when we construct an electrochemical cell and calculate the voltage, we simply take the difference between the half cell potentials and do not worry about the number of electrons in the reaction. For example, for the displacement reaction in which silver ions are reduced by copper metal, the reaction is:
\(\ce{2Ag^{+}_{(aq)} + Cu_{(s)} = 2Ag_{(s)} + Cu^{2+}_{(aq)}}\)
The two half-cell reactions are:
\(Ag^{+}_{(aq)} + e^{-} =Ag_{(s)}\: \: + 0.80V\)
\(Cu^{2+}_{(aq)} + 2e^{-} = Cu_{(s)} \: \: + 0.34V\)
and the standard potential \(E^{o} = +0.80 - 0.34V = + 0.46V\)
The reason we don't need to multiply the Ag potential by 2 is that Eo is a measure of the free energy change per electron. Dividing the free energy change by the number of electrons (see below) makes Eo an intensive property (like pressure, temperature, etc.).
Relationship between E and ΔG. For systems that are in equilibrium, \( \Delta G^{o} = -nFE^{o}_{cell}\), where n is number of moles of electrons per mole of products and F is the Faraday constant, ~96485 C/mol. Here the o symbol indicates that the substances involved in the reaction are in their standard states. For example, for the water electrolysis reaction, the standard states would be pure liquid water, H+ at 1M concentration (or more precisely, at unit activity), and O2 and H2(g) at 1 atmosphere pressure.
More generally (at any concentration or pressure), \(\Delta G = - nFE\), where
\[E = E^{o} - \frac{RT}{nF} * lnQ\],
or at 298 K
\[E=E^{o} - \frac{0.0592}{n} * \log Q\]
where Q is the concentration ratio of products over reactants, raised to the powers of their coefficients in the reaction. This equation (in either form) is called the Nernst equation. The second term in the equation, when multiplied by -nF, is RT*lnQ. This is the free energy difference between ΔG and ΔG°. We can think of this as an entropic term that takes into account the positive entropy change of dilution, or the negative entropy change of concentrating a reactant or product, relative to its standard state.
Using the Nernst equation
Example 1:
For the half reaction \(\ce{2H^{+} + 2e^{-} = H_{2}}\), E°1/2 = 0.000 V (by definition)
What is E1/2 at pH 5 and PH2 = 1 atm?
\(pH = -\log[H^{+}] = 5\), so [H+] = 10-5 M
\[E=E^{o} - \frac{0.0592}{2} * \log\frac{P_{H2}}{(H^{+})^{2}} = E^{o} - \frac{0.0592}{2} * \log(10^{5})^{2} = E^{o} - \frac{0.0592}{2}(10) = 0.000-0.296=-0.296V\]
Example 2:
What is the potential of a fuel cell (a galvanic H2/O2 cell) operating at pH 5?
Overall reaction: \(\ce{2H2_{(g)} + O2_{(g)} = 2H2O_{(l)}}\)
In this reaction, H2 is oxidized to H+ and O2 is reduced to H2O. According to our convention, we write out and balance both half-cell reactions as reductions. For convenience, we do this in acid. (It is left as an exercise to the interested reader to try to work the problem in base)
Half cell reactions:
\(\ce{2H2_{(g)} = 4H^{+} + 4e^{-}}\)
\(\ce{O2_{(g)} + 4H^{+}_{(aq)} + 4e^{-} = 2H2O_{(l)}}\)
|
Toyota fuel cell hybrid bus. The bus runs on electrical energy obtained directly from the H2/O2 reaction. Individual fuel cells are connected in series to make a power train that charges a battery pack and drives an electric motor. Although the standard potential of the reaction is 1.23 V, because of kinetic overpotentials each fuel cell in the power train operates at a voltage of about 0.70 V. Despite this energy loss, the fuel cell system is still about twice as efficient as a combustion engine performing the same reaction. |
To solve this problem we need to find the difference between the H2/ H+ and O2/H2O half cell potentials at pH 5.
\(\ce{2H^{+} + 2e^{-} -> H2}\) E°1/2 = 0.000 V
Like all standard potentials, this is written as a reduction. We need to reverse it and change the sign of Eo since H2 is being oxidized:
\(\ce{H2 -> 2H^{+} + 2e^{-}}\) E°1/2 = -0.000 V
and add the standard potential of the substance being reduced at the cathode:
\(\ce{O2 + 4H^{+} + 4e^{-} -> 2H2O}\) E°1/2 = +1.229 V
The difference between the two standard half cell potentials is +1.229 - 0.000 = +1.229 V
E°cell = +1.229 Volts
We now use the Nernst equation to account for the fact that H+ is not in its standard state:
\[ E_{cell} = E^{o} -\frac{0.0592}{4} * log \frac{[H^{+}]^{4}}{P_{O2}P^{2}_{H2}[H^{+}]^{4}} = E^{o} -\frac{0.0592}{4}* log(1) = E^{o} = + 1.229V\]
Note that the value of Ecell does not change with pH since both couples shift -59.2 mV/pH according to the Nernst equation. This is the consequence of the fact that the number of electrons equals the number of protons in each of the half cell reactions. Another way to rationalize this result is to remember that the overall reaction (2H2 + O2 = 2H2O) does not involve H+ as a reactant or product, so ΔG and E should be independent of pH.
We can plot the shift in the H2/H+ and O2/H2O half-cell potentials with pH on a potential-pH diagram (also called a Pourbaix diagram) as shown below. The pH-dependent potentials of the H2 and O2 couples are shown as dotted lines. Notice that the potential difference between them is always 1.23 V. The dark circles represent the standard potentials.
|
Pourbaix diagram for water. |
Pourbaix diagrams are essentially electrochemical phase diagrams, which plot regions of thermodynamic stability for redox-active substances. As in other kinds of phase diagrams, the lines represent conditions under which two phases coexist in equilibrium. The shaded area in the water Pourbaix diagram represents the conditions of potential and pH where liquid water is stable relative to hydrogen or oxygen. Outside the shaded region, water is thermodynamically unstable and is reduced to H2(g) or oxidized to O2(g). Although these processes are spontaneous in the thermodynamic sense (for example, water is unstable in the presence of Pb4+, Cl2, Fe, Zn, or Al), they are kinetically slow and require catalysis to proceed.




