3.2: Brønsted and Lewis Acids and Bases

Three theories of acids and bases

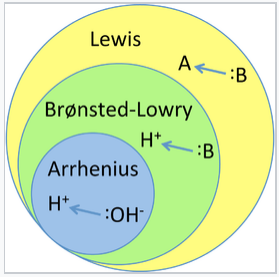
There are three major classifications of substances known as acids or bases. The Arrhenius definition states that an acid produces H⁺ in solution and a base produces OH^-. This theory was developed by Svante Arrhenius in 1883. Later, two more sophisticated and general theories were proposed. These are the Brønsted-Lowry and the Lewis definitions of acids and bases. The relationship between these theories is illustrated in the figure below.

Illustration of the hierarchy of acid-base theories. Arrhenius acids and bases are a sub-class of Brønsted acids and bases, which are themselves a subclass of Lewis acids and bases.

The Arrhenius theory, which is the simplest and least general description of acids and bases, includes acids such as HClO₄ and bases such as NaOH or Mg(OH)₂. This theory successfully describes how acids and bases react with each other to make water and salts. However, it does not explain why some substances that do not contain hydroxide ions, for example F^- and NO₂^-, can make basic solutions in water. The Brønsted-Lowry definition of acids and bases addresses this problem. In this theory an acid is a substance that can release a proton (like in the Arrhenius theory) and a base is a substance that can accept a proton. A basic salt such as Na⁺F^- generates OH^- ions in water by taking protons from water itself (to make HF):

\[\ce{F^{-}_{(aq)} + H2O_{(l)} <=> HF_{(aq)} + OH^{-}}\]

When a Brønsted acid dissociates, it increases the concentration of hydrogen ions in the solution, [H⁺]; conversely, Brønsted bases dissociate by taking a proton from the solvent (water) to generate [OH^-].

Acid Dissociation: \(\ce{HA_{(aq)} <=> A^{-}_{(aq)} + H+_{(aq)}}\)

\[K_{a}= \frac{[A^{-}][H^{+}]}{[HA]}\]

Base dissociation: \(\ce{B_{(aq)}+ H2O_{(l)} <=> HB+_{(aq)} + OH^{-}+{(aq)}}\)

\[K_{b}= \frac{[HB^{+}][OH^{-}]}{[B]}\]

Conjugate acids and bases

One important consequence of these equilibria is that every acid (HA) has a conjugate base (A-), and vice-versa. In the base dissociation equilibrium above the conjugate acid of base B is HB⁺.

For a given acid or base, these equilibria are linked by the water dissociation equilibrium:

\[\ce{H2O_{(l)} <=> H^{+}_{(aq)} + OH^{-}_{(aq)}}\]

\[K_{w} = [H^{+}][OH^{-}]\]

for which the equilibrium constant K_w is 1.00 x 10^-14 at 25°C. It can be easily shown that the product of the acid and base dissociation constants K_a and K_b is K_w.

Strong and weak acids and bases

Acids and bases that dissociate completely are said to be strong:

\[\ce{HClO4_{(aq)} -> H^{+}_{(aq)} + ClO4^{-}_{(aq)}}\]

\[\ce{HBr_{(aq)} -> H^{+}_{(aq)} + Br^{-}_{(aq)}}\]

\[\ce{CH3O^{-}_{(aq)} + H2O_{(l)} -> CH3OH_{(aq)} + OH^{-}_{(aq)}}\]

\[\ce{NH2^{-}_{(aq)} + H2O_{(l)} -> NH3_{(aq)} + OH^{-}_{(aq)}}\]

Here the right-handed arrow (→) implies that the reaction goes to completion. That is, a 1.0 M solution of HClO₄ in water actually contains 1.0 M H⁺(aq) and 1.0 M ClO₄^-(aq), and very little undissociated HClO₄.

Conversely, weak acids such as acetic acid (CH₃COOH) and weak bases such as ammonia (NH₃) dissociate only slightly in water - typically a few percent, depending on their concentration and the values of K_a and K_b - and exist mostly as the undissociated molecules.

Antacid tablets typically contain calcium salts of the bicarbonate ion (HCO3^-), a weak base. Its conjugate acid, carbonic acid (H2CO3) is a weak acid. The acid-base equilibrium between carbonic acid and bicarbonate is important in maintaining blood pH.

Example

Household ammonia is a solution of NH₃ in water that ranges from about 5-10% by weight. Let’s calculate the percent ionization and the pH of the solution.

Solution

For a solution that is 8% ammonia by weight, assuming that the density is about the same as that of liquid water, the analytical concentration of ammonia is (80 g/L) / (17 g/mol) = 4.7 M.

The other thing we need to know to solve this problem is the base dissociation constant, \(K_b\).

\(\ce{NH3 + H2O <=> NH4^{+} + OH^{-}} \; K_b = 1.8 \times 10^{-5}\)

We can solve this problem rigorously by invoking both charge balance ([H⁺] + [NH₄⁺] = [OH^-]) and mass balance (4.7 M = [NH₃] + [NH₄⁺]) and using \(K_W\)= [H⁺][OH^-]. But because the algebra becomes complicated with that method - leading to a cubic equation that is hard to solve - we’ll invoke two simplifying assumptions:

\([NH_{4}^{+}] \approx [OH^{-}] \gg [H^{+}]\) (which is a reasonable assumption for a basic solution)

and

\([NH_{3}] \gg [NH_{4}^{+}]\) (also reasonable if the percent ionization is small)

Now we can write:

\([NH_{4}^{+}][OH^{-}] \approx [OH^{-}]^{2} = (4.7M)(K_{b})= 8.4 \times 10^{-5}\)

\([OH^{-}]= 9.2 \times 10^{-3} M \; (\approx [NH_{4}^{+}]), \: [H^{+}] = \frac{K_{w}}{[OH^{-}]} = 1.1 \times 10^{-12}M, \: \textbf{ pH = 11.97}\)

The percent ionization is:

\(100\% \times 9.2 \times 10^{-3}M / 4.7M = \textbf{0.19%}\)

This example illustrates that it is technically incorrect to label a bottle of aqueous ammonia as “ammonium hydroxide,” since only about 2/10 of one percent of the weak base exists in that form.

Conjugate acids and bases

A common misconception is that strong acids have weak conjugate bases, and that weak acids have strong conjugate bases. It is easy to see that this is incorrect by remembering that K_aK_b = K_w. Our definition of a strong acid or base is that K >> 1, i.e., that the substance dissociates completely. Our definition of a weak acid or base is 1 > K > K_w. It follows that if K_a >> 1 (strong) then K_b cannot be > K_w (weak).

In fact, strong acids such as HCl dissociate to produce spectator ions such as Cl^- as conjugate bases, whereas weak acids produce weak conjugate bases. This is illustrated below for acetic acid and its conjugate base, the acetate anion. Acetic acid is a weak acid (K_a = 1.8 x 10^-5) and acetate is a weak base (\(K_{b} = \frac{K_{w}}{K_{a}} = 5.6 \times 10^{10}\))

The strength of a conjugate acid/base varies inversely with the strength or weakness of its parent acid or base. Any acid or base is technically a conjugate acid or conjugate base also; these terms are simply used to identify species in solution (i.e acetic acid is the conjugate acid of the acetate anion, a base, while acetate is the conjugate base of acetic acid, an acid).

Neutral oxyacids (H₂SO₄, H₃PO₄, HNO₃, HClO₂, etc.) can be classified as strong or weak following a simple rule first noted by Linus Pauling. If the number of oxygen atoms exceeds the number of hydrogen atoms by two or more, then the acid is strong; otherwise it is weak. For example HClO₄ and HClO₃, where the difference is 3 and 2, respectively, are both strong acids. HNO₂ and HClO₂ are both weak because the difference is 1 in both cases. For weak acids, the relative strength depends on this difference (i.e., HClO₂ is a stronger weak acid than HOCl) and on the electronegativity of the central atom (HOCl is stronger than HOI).

Acids that can donate more than one proton are called polyprotic acids. For example, sulfuric acid, H₂SO₄, is a strong acid that has a conjugate base that actually happens to be a weak acid itself. This means that every mole of H₂SO₄ in aqueous solution donates more than 1 mole of protons. Carbonic acid (H₂CO₃) and phosphoric acid (H₃PO₄) are weak polyprotic acids. Typically, the sequential pK_a's of polyprotic acid are separated by about 5 pH units, because it becomes progressively more difficult to remove protons as the ion becomes more negatively charged. For example, the three pK_a's of phosphoric acid are 2.15, 7.20, and 12.35.

Amphoteric compounds

Some substances can act either as an acid and as a base. An example is water. H₂O molecules may either donate a hydrogen ion or accept one. This property makes water an amphoteric solvent. In the situation where an acid dissociates in solution, water is acting as a base. Conversely, water acts as an acid when bases dissociate. The strongest acid we can make in H₂O is H⁺ (aq), and the strongest base we can make in H₂O is OH^- (aq).

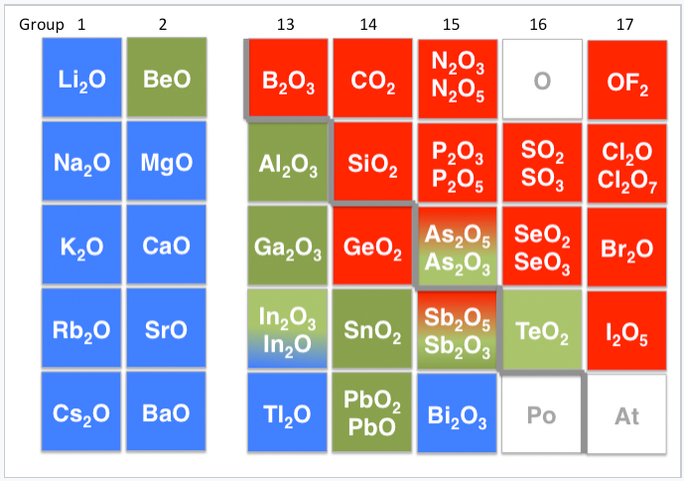
Other examples of amphoteric compounds are oxides and hydroxides of elements that lie on the border between the metallic and non-metallic elements in the periodic table. For example, aluminum hydroxide (Al(OH)₃) is insoluble at neutral pH, but can accept protons in acid to make [Al(H₂O)₆]³⁺ or accept an OH^- ion in base to form Al(OH)₄^- ions. Consequently, aluminum oxide is soluble in acid and in base, but not neutral water. Other examples of amphoteric oxides are BeO, ZnO, Ga₂O₃, Sb₂O₃, and PbO. Increasing the oxidation state of a metal increases the acidity of its oxide by withdrawing electron density from the oxygen atoms. Thus, Sb₂O₅ is acidic, but Sb₂O₃ is amphoteric.

Periodic table showing basic (blue), amphoteric (green) and acidic (red) oxides. The metal-nonmetal boundary is indicated by the gray staircase line.

Solvent leveling

Solvent leveling is an effect that occurs when a strong acid is placed in a solvent such as (but not limited to) H₂O. Because strong acids donate their protons to the solvent, the strongest possible acid that can exist is the conjugate acid of the solvent. In aqueous solution, this is H₃O⁺. This means that the strength of acids such as HCl and HBr cannot be differentiated in water as they both are dissociated 100% to H₃O⁺. In the context of our discussion of conjugate bases above, we would say that both Cl^- and Br^- are spectator ions in water: neither one is a strong enough base to accept a proton from H₃O⁺. In order to differentiate the acidities of strong acids such as HClO₄ and HCl, or the basicities of strong bases such as CH₃O^- and NH₂^-, we must typically work in non-aqueous solvents, as explained below.

Nonaqueous solutions

The Brønsted theory encompasses any type of solvent that can donate and accept H⁺ ions, not just aqueous solutions. The strength of an acid or a base varies depending on the solvent. Non-aqueous acid-base chemistry follows similar rules to those developed for acids and bases in water. For example in liquid ammonia, the solvent autodissociates in the reaction:

\[\ce{2NH3_{(l)} <=> NH4^{+} + NH2^{-}}\]

This equilibrium is analogous to the autodissociation of water, but has a smaller equilibrium constant (K ≈ 10^-30). It follows by analogy to water that NH₄⁺ is the strongest acid and NH₂^- is the strongest base that can exist in liquid ammonia. Because ammonia is a basic solvent, it enhances the acidity and suppresses the basicity of substances dissolved in it. For example, the ammonium ion (NH₄⁺) is a weak acid in water (K_a = 6 x 10^-10), but it is a strong acid in ammonia. Similarly, acetic acid is weak in water but strong in ammonia. Solvent leveling in fact makes HCl, CH₃COOH, and NH₄Cl all strong acids in ammonia, where they have equivalent acid strength.

Strong acids that are leveled in water have different acid strengths in acidic solvents such as HF or anhydrous acetic acid. For example, acid dissociation of HX in acetic acid (CH₃COOH) involves protonating the solvent to make its conjugate acid (CH₃COOH₂⁺) and the X^- anion. Because CH₃COOH₂⁺ is a stronger acid that H₃O⁺, the anion X^- (which is a spectator in water) can become a weak base in CH₃COOH:

\[\ce{HX + CH3COOH <=> CH3COOH2^{+} + X^{-}}\]

It follows that acidic solvents magnify the Brønsted basicities of substances that cannot accept protons in water. Conversely, basic solvents magnify the acidity of substances that cannot donate a proton to OH^-.

The acidity and basicity of non-aqueous solvents is difficult to quantify precisely, but one good relative measure is the Hammett acidity function, H_o. H_o is defined analogously to pH according to the Henderson-Hasselbach equation:

\[H_{o} = pK_{a} + \log(\frac{[base]}{[conjugate \: acid]})\]

For non-aqueous solvents, or for acidic or basic compounds in dissolved in solvents that do not themselves dissociate, H_o is a rough measure of the pH of the solvent or compound in question. Anhydrous HF and H₂SO₄ have H_o values of approximately -10 and -12 respectively.

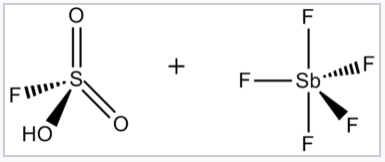
Superacids and superbases. The term superacid was originally coined by James Bryant Conant in 1927 to describe acids that were stronger than conventional mineral acids.^[1] George A. Olah prepared the so-called magic acid, so-named for its ability to attack hydrocarbons, by mixing antimony pentafluoride (SbF₅) and fluorosulfonic acid (FSO₃H). The name was coined after a candle was placed in a sample of magic acid. The candle dissolved, showing the ability of the acid to protonate hydrocarbons, which under aqueous acidic conditions cannot be protonated.

Magic acid is made by mixing FSO3H and SbF5. Their reaction generates the H2SO3F^+ cation, which can protonate hydrocarbons.

At 140 °C , FSO₃H–SbF₅ converts methane into the tertiary-butyl carbocation, a reaction that begins with the protonation of methane:^[2]

\[\ce{CH4 + H^{+} -> CH5^{+}}\]

\[\ce{CH5^{+} -> CH3^{+} + H2}\]

\[\ce{CH3^{+} + 3CH4 -> (CH3)3C^{+} + 3H2}\]

Fluoroantimonic acid, HSbF₆, can produce solutions with H₀ down to –28.^[3] Fluoroantimonic acid is made by combining HF and SbF₅. In this system, HF releases its proton (H⁺) concomitant with the binding of F⁻ by antimony pentafluoride, which (as described below) is a Lewis acid. The resulting anion (SbF₆-) is both a weak nucleophile and an extraordinarily weak base.

Superacids are useful in reactions such as the isomerization of alkanes. Industrially, anhydrous acid-exchanged zeolites, which are superacid catalysts, are used on a massive scale to isomerize hydrocarbons in the processing of crude oil to gasoline. Superbases such as lithium diethylamide (LiNEt₂), alkyllithium compounds (RLi), and Grignard reagents (RMgX) useful in a broad range of organic reactions. LiNEt₂ deprotonates C-H bonds to generate reactive carbanions. RLi and RMgX are powerful nucleophiles.

The use of superbases in nonaqueous media allows us to rank the acidities (and measure the pKa's) of different classes of molecules. This ranking is particularly important in understanding the reactions of organic molecules. Note that the order of acidities for hydrocarbons is alkynes >> alkenes, aromatics >> alkanes. This ordering has to do with the hybridization of the carbon atom that forms the carbanion. The negatively charged lone pair of the carbanion is stabilized in orbitals that have high s character (e.g., sp vs. sp² or sp³). This is because s orbitals have finite probability density at the nucleus and "feel" the positive nuclear charge (thereby stabilizing the extra negative charge on carbon) more than p orbitals. Resonance effects also stabilize carbanions. Thus, cyclopentadiene is more acidic than even an alkyne because the negative charge is delocalized over the entire (aromatic) C₅H₅^- ring when the C₅H₆ is deprotonated.

name	formula	structural formula	pKa
Methane	CH4		56
Propene	C3H6		44
Benzene	C6H6		43
Acetylene	C2H2		25
Cyclopentadiene	C5H6		18

Table 1. Carbon acid acidities in pKa in DMSO ^[4].

Acid-base equilibria in molten salts

When a solid salt melts, it forms a solution of the cations and anions. For example, KOH melts at temperatures above 400 °C and dissociates into K⁺ and OH^- ions which can act as a solvent for chemical reactions. Because of the autodissociation of the OH^- solvent, water is always present in a molten KOH flux, according to the acid-base equilibrium:

\[\ce{2 OH^{-} <=> H2O + O^{2-}}\]

It follows that in this very basic solvent, water (the conjugate acid of the solvent) is the strongest acid that can exist. The conjugate base of the solvent, O^2-, is the strongest base. This autodissociation equilibrium allows for the acidity of a flux to be easily tuned through the addition or boiling off of water. A "wet" flux is more acidic, and can dissolve metal oxides that contain the basic O^2- anion. Conversely a "dry" flux is more basic and will cause oxides to precipitate. Molten hydroxide fluxes can thus be used in the synthesis of oxide crystals, such as the perovskite superconductor (K_1-XBa_XBiO₃).^[5]. Eutectic mixtures of NaOH and KOH are relatively low melting (≈ 200 °C) and can be used as solvents for crystallizing a variety of basic oxides.

Lewis Acids and Bases

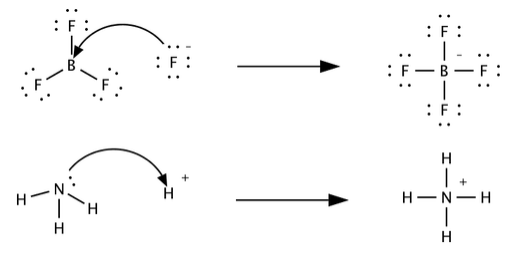
The Lewis classification of acids and bases is broader than the Brønsted-Lowry definition, and encompasses many more substances. Whereas the Brønsted-Lowry and the Arrhenius classifications are based on transfer of protons, Lewis acidity and basicity are based on the sharing of an electron pair. Lewis acids can accept an electron pair, while Lewis bases can donate an electron pair. This definition encompasses the Brønsted-Lowry definition, in that H⁺ is an electron pair acceptor (when interacting with a base), and a base is an electron pair donor in its interaction with H⁺. This is illustrated below for the protonation of ammonia.

Boron trifluoride, BF₃ acts as a Lewis acid when it combines with a basic ion or molecule that can donate an electron pair. Such a reaction is shown below.

\[\ce{BF3 + F^{-} <=> BF4^{-}

Here, the acid is BF₃ and the base is F^-. This acid-base reaction allows boron (which is electron-deficient in BF₃) to complete its octet. Similarly, AlCl₃ is a Lewis acid that can react with Cl^- (a Lewis base) to make the Lewis "salt" AlCl₄^-. Note that in water Cl^- is a spectator ion (a weaker base than the solvent) in Brønsted acid-base reactions.

Additional examples of Lewis acid base reactions. In each, try to identify the acid, the base, and the salt, based on the concept that the base is the molecule or ion that donates an electron pair. In cases where you are not sure, it may help to draw the VSEPR structures of the molecules:

\(\ce{I2 + I^{-} <=> I3^{-}}\)

\(\ce{AuCl3 + Cl^{-} <=> [AuCl4]^{-}}\)

\(\ce{Fe^{3+} + 6H2O <=> [Fe(H2O)6]^{3+}}\)

\(\ce{TiF4 + 2F^{-} <=> [TiF6]^{2-}}\)

\(\ce{SF4 + SbF5 <=>SSbF9}\)

In other Lewis acid base reactions both acid and base are molecules and the product is referred to as an adduct.

\(\ce{(CH3)3B + N(CH3)3 -> (CH3)3B-N(CH3)3}\)

\(\ce{I2 + S(CH3)2 -> I2-S(CH3)2}\)

\(\ce{C5N5N + Cu(HFacac)2 -> C5N5N-Cu(HFacac)2}\)

Lewis acidity is the basis for coordination chemistry, a topic we will discuss in more detail in Chapter 5. This is because coordination chemistry involves metal ions that are Lewis acids, which bond to ligands that are Lewis bases.

Determining the strength of metal ion Lewis acids

There are three determining factors in the Lewis acid strength of a metal ion:
1. The higher positive charge on the metal, the more acidic it is. For example, Al³⁺ and Fe³⁺ are good Lewis acids and their salts make acidic solutions in water, but K⁺and Na⁺ are not.
2. The smaller the atomic radius of the metal ion, the more acidic it is. Going down the periodic table, the Lewis acidity of metal ions decreases (e.g., Al³⁺ > Ga³⁺ > In³⁺) because the ionic radius increases.
3. For transition metal ions, more electronegative metals tend to make stronger Lewis acids. The electronegativity has maxima at W and Au in the 5d series, so metal ions near in that part of the periodic table are good Lewis acids.

Molecules with five coordinate geometries (e.g., PCl₅, AsF₅, SbF₅) are typically strong Lewis acids, because when accepting another pair of electrons from a base, they form an octahedral molecule or anion. Neither of the common five-coordinate geometries (trigonal bipyramidal or square pyramidal) is efficient in terms of packing. The Lewis acid-base reaction forms an additional bond with a relatively small energetic penalty of stretching the existing bonds:

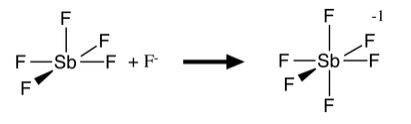
Because F^- is a good Lewis base, and also a small anion, it can form stable octahedral anions with both main group elements and transition metals. For this reason, TiO₂ and SiO₂ dissolve in HF (but are unreactive with aqueous HCl and other strong acids):

\[\ce{TiO2 + 4HF + 2F^{-} <=> TiF6^{2-} + 2H2O}\]

\[\ce{SiO2 + 4HF + 2F^{-} <=> SiF6^{2-} + 2H2O}\]

Lewis bases stabilize high oxidation states.

An interesting example of using Lewis acid-base chemstry to drive reactions is the chemical synthesis of fluorine gas, which was devised by Karl O. Christe in 1986.^[6] Christe at the time was organizing a symposium to commemorate the 100th anniversary of the isolation of elemental fluorine by Henri Moissan, which Moissan did in 1886 by electrolyzing a solution of anhydrous HF. 100 years later, there was still no direct (non-electrochemical) synthesis of F₂. Christe's reaction scheme followed two steps. The first was the known synthesis of K₂MnF₆ from KMnO₄:

\[\ce{4MnO4^{-}_{(aq)} + 10H2O_{(l)} + 24F^{-}_{(aq)} -> 4MnF6^{2-}_{(aq)} = 3O2_{(g)} + 20OH^{-}_{(aq)}}\]

\[\ce{2K^{+}_{(aq)} + MnF6^{2-}_{(aq)} -> K2MnF6_{(s)}}\]

The second step involved reacting K₂MnF₆ with the powerful Lewis acid SbF₅, to make metastable MnF₄, which decomposes spontaneously to MnF₃ and fluorine gas:

\[\ce{K2MnF6_{(s)} + 2SbF5_{(l)} -> 2KSbF6_{(s)} + MnF4_{(s)}}\]

\[\ce{MnF4_{(s)} -> MnF3_{(s)} + \frac{1}{2}F2_{(g)}}\]

This reaction teaches us something interesting and important about the connection between acid-base and redox chemistry. Acids tend to stabilize low oxidation states, and bases stabilize high oxidation states (We will see this again soon in Chapter 4, in the context of Pourbaix diagrams). Mn is stable in the +4 oxidation state in K₂MnF₆, where it is surrounded by six basic F^- anions. However, the highest stable neutral fluoride of Mn is MnF₃, and MnF₄ (transiently formed from K₂MnF₆) spontaneously decomposes to generate fluorine.

Oxide is a better base than fluoride. Interestingly, Mn can lose all its valence electrons to form Mn⁷⁺ in the permanganate ion, MnO₄^-. Here the 7+ oxidation state is stabilized electrostatically by coordination to four O^2- ions, and by the overall -1 charge on the MnO₄^- anion. Because of its 2- charge, O^2- is a stronger base and a better ion for stabilizing high oxidation states than F^-. This is a general trend among transition metals: the highest oxidation state is usually reached in the oxide, not in the fluoride, despite the fact that F is a more electronegative element than O. For example, Cr⁶⁺ is stable in the CrO₄^2- and Cr₂O₇^2- anions, but not in any neutral fluoride or fluoroanion. The +8 oxidation state occurs in RuO₄ and OsO₄, but not in any fluoride of Ru or Os.