2.11: Chains and Rings of π-Conjugated Systems
- Page ID
- 184897
 Ethylene: The π system is analogous to σ-bonding in H2
Ethylene: The π system is analogous to σ-bonding in H2
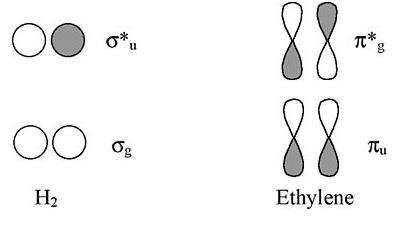
Viewed from the top or bottom, the ethylene π-orbitals look like the H2 σ orbitals. Thus we can map solutions from chains and rings of H atoms onto chains and rings of π-orbitals (as we did for the three-orbital case of O3).
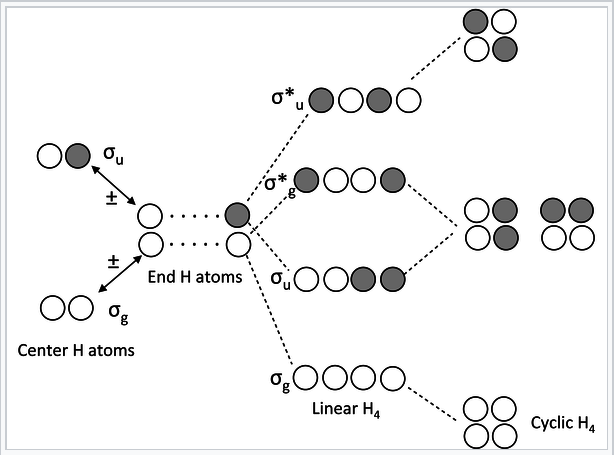
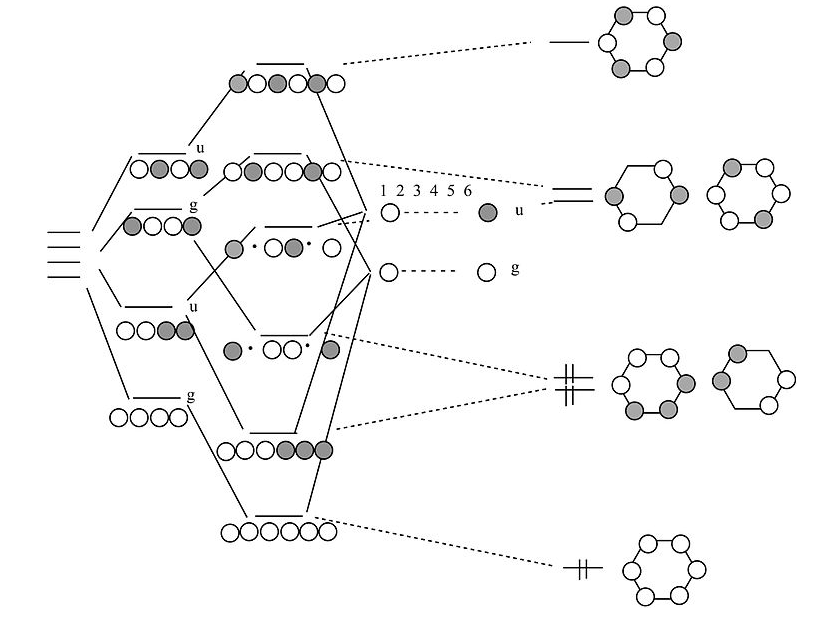
Chains and rings of four H atoms or π-orbitals (H4 or butadiene):
|
MO diagram for H4 or butadiene |
A few notes about this MO diagram:
- In the linear form of the molecule, the combination of AOs makes a ladder of evenly spaced energy levels that alternate g – u – g – u …. Each successive orbital has one more node. This is a general rule for linear chains of σ or π orbitals with even numbers of atoms.
- In the cyclic form of the molecule, there is one non-degenerate orbital at the bottom, one at the top, and a ladder of doubly degenerate orbitals in between. This is also a general rule for cyclic molecules with even numbers of atoms. This is the origin of the 4n+2 rule for aromatics.
- H4 has four valence electrons, and by analogy butadiene has four π-electrons. These electrons fill the lowest two MOs in the linear form of the molecule, corresponding to two conjugated π-bonds in butadiene (H2C=CH-CH=CH2).
- In the cyclic form of the molecule, the degenerate orbitals are singly occupied. The molecule can break the degeneracy (and lower its energy) by distorting to a puckered rectangle. This is a general rule for anti-aromatic cyclic molecules (4n rule). Thus cyclobutadiene should be anti-aromatic and have two single and two double bonds that are not delocalized by resonance.
Cyclobutadiene is actually a very unstable molecule because it polymerizes to relieve ring strain. Sterically hindered derivatives of the molecule do have the puckered rectangular structure predicted by MO theory.
Benzene π-orbitals:
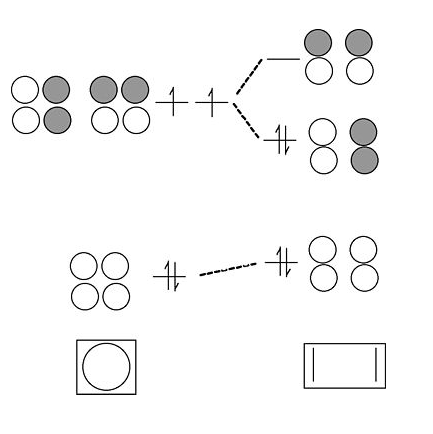
How do we get from a 4-atom to 6-atom chain?
By analogy to the process we used to go from a 2-atom chain to a 4-atom chain, we now go from 4 to 6. We start with the orbitals of the 4-atom chain, which form a ladder of g and u orbitals. Then we make g and u combinations of the two atoms that we are adding at the ends. By combining g's with g's and u's with u's, we end up with the solutions for a string of 6 atoms. Closing these orbitals into a loop gives us the π molecular orbitals of the benzene molecule. The result is three π bonds, as we expected. Benzene fits the 4n+2 rule (n=2) and is therefore aromatic.
Here we have used the isolobal analogy to construct MO diagrams for π-bonded systems, such as ethylene and benzene, from combinations of s-orbitals. It raises the interesting question of whether the aromatic 4n+2 rule might apply to s-orbital systems, i.e., if three molecules of H2 could get together to form an aromatic H6molecule. In fact, recent studies of hydrogen under ultra-high pressures in a diamond anvil cell show that such structures do form. A solid hydrogen phase exists that contains sheets of distorted six-membered rings, analogous to the fully connected 2D network of six-membered rings found in graphite or graphene.[6]
It should now be evident from our construction of MO diagrams for four- and six-orbital molecules that we can keep adding atomic orbitals to make chains and rings of 8, 10, 12... atoms. In each case, the g and u orbitals form a ladder of MOs. At the bottom rung of the ladder of an N-atom chain, there are no nodes in the MO, and we add one node for every rung until we get to the top, where there are N-1 nodes. Another way of saying this is that the wavelength of an electron in orbital x, counting from the bottom (1,2,3...x,...N), is 2Na/x, where a is the distance between atoms. We will find in Chapters 6 and 10 that we can learn a great deal about the electronic properties of metals and semiconductors from this model, using the infinite chain of atoms as a model for the crystal.