16.3: Precipitation and the Solubility Product
- Page ID
- 41632
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define Ksp, the solubility product.
- Explain solid/solution equilibria using \(K_{sp}\) and Qsp.
- Calculate molarity of saturated solution from Ksp.
- Calculate \(K_{sp}\) from molarity of saturated solution.
Precipitation reactions occur when cations and anions in aqueous solution combine to form an insoluble ionic solid called a precipitate. Whether or not such a reaction occurs can be determined by using the solubility rules for common ionic solids. Because not all aqueous reactions form precipitates, one must consult the solubility rules before determining the state of the products and writing a net ionic equation. The ability to predict these reactions allows scientists to determine which ions are present in a solution, and allows industries to form chemicals by extracting components from these reactions.
Properties of Precipitates
Precipitates are insoluble ionic solid products of a reaction, formed when certain cations and anions combine in an aqueous solution. The determining factors of the formation of a precipitate can vary. Some reactions depend on temperature, such as solutions used for buffers, whereas others are dependent only on solution concentration. The solids produced in precipitate reactions are crystalline solids, and can be suspended throughout the liquid or fall to the bottom of the solution. The remaining fluid is called supernatant liquid (or just the supernate). The two components of the mixture (precipitate and supernate) can be separated by various methods, such as filtration, centrifuging, or decanting.
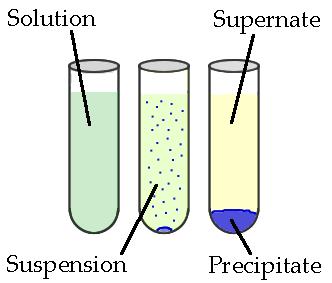
Figure \(\PageIndex{1}\): Above is a diagram of the formation of a precipitate in solution. (Public Domain; ZabMilenko)
The use of solubility rules require an understanding of the way that ions react. Most precipitation reactions are single replacement reactions or double replacement reactions. A double replacement reaction occurs when two ionic reactants dissociate and bond with the respective anion or cation from the other reactant. The ions replace each other based on their charges as either a cation or an anion. This can be thought of as a double displacement reaction where the partners "switching; that is, the two reactants each "lose" their partner and form a bond with a different partner:

A double replacement reaction is specifically classified as a precipitation reaction when the chemical equation in question occurs in aqueous solution and one of the of the products formed is insoluble. An example of a precipitation reaction is given below:
\[\ce{CdSO4(aq) + K2S (aq) \rightarrow CdS (s) + K2SO4(aq)}\]
Both reactants are aqueous and one product is solid. Because the reactants are ionic and aqueous, they dissociate and are therefore soluble. However, there are six solubility guidelines used to predict which molecules are insoluble in water. These molecules form a solid precipitate in solution.
Whether or not a reaction forms a precipitate is dictated by the solubility rules. These rules provide guidelines that tell which ions form solids and which remain in their ionic form in aqueous solution. The rules are to be followed from the top down, meaning that if something is insoluble (or soluble) due to rule 1, it has precedence over a higher-numbered rule.
- Salts formed with group 1 cations and \(\ce{NH_4^{+}}\) cations are soluble. There are some exceptions for certain \(Li^+\) salts.
- Acetates (\(\ce{C2H3O2^{-}}\)), nitrates (\(\ce{NO3^{-}}\)), and perchlorates (\(\ce{ClO4^{-}}\)) are soluble.
- Bromides, chlorides, and iodides are soluble.
- Sulfates (\(\ce{SO4^{2-}}\)) are soluble with the exception of sulfates formed with \(\ce{Ca^{2+}}\), \(\ce{Sr^{2+}}\), and \(\ce{Ba^{2+}}\).
- Salts containing silver, lead, and mercury (I) are insoluble.
- Carbonates (\(\ce{CO3^{2-}}\)), phosphates (\(\ce{PO4^{3-}}\)), sulfides, oxides, and hydroxides (\(\ce{OH^{-}}\)) are insoluble. Sulfides formed with group 2 cations and hydroxides formed with calcium, strontium, and barium are exceptions.
If the rules state that an ion is soluble, then it remains in its aqueous ion form. If an ion is insoluble based on the solubility rules, then it forms a solid with an ion from the other reactant. If all the ions in a reaction are shown to be soluble, then no precipitation reaction occurs.
Net Ionic Equations
To understand the definition of a net ionic equation, recall the equation for the double replacement reaction. Because this particular reaction is a precipitation reaction, states of matter can be assigned to each variable pair:
\[\color{blue}{A}\color{red}{B}\color{black} (aq) + \color{blue}{C}\color{red}{D}\color{black} (aq) → \color{blue}{A}\color{red}{D}\color{black} (aq) \color{black}+ \color{blue}{C}\color{red}{B}\color{black} (s) \]
The first step to writing a net ionic equation is to separate the soluble (aqueous) reactants and products into their respective cations and anions. Precipitates do not dissociate in water, so the solid should not be separated. The resulting equation looks like that below:
\[\color{blue}{A}^+ \color{black} (aq) + \color{red}{B}\color{black}^- (aq) + \color{blue}{C}\color{black}^+ (aq) + \color{red}{D}^-\color{black} (aq) → \color{blue}{A}^+\color{black} (aq) + \color{red}{D}^-\color{black} (aq) + \color{blue}{C}\color{red}{B}\color{black} (s) \]
In the equation above, A+ and D- ions are present on both sides of the equation. These are called spectator ions because they remain unchanged throughout the reaction. Since they go through the equation unchanged, they can be eliminated to show the net ionic equation:
\[ \color{red}{B}\color{black}^- (aq) + \color{blue}{C}\color{black}^+ (aq) → + \color{blue}{C}\color{red}{B}\color{black} (s) \]
The net ionic equation only shows the precipitation reaction. A net ionic equation must be balanced on both sides not only in terms of atoms of elements, but also in terms of electric charge. Precipitation reactions are usually represented solely by net ionic equations. If all products are aqueous, a net ionic equation cannot be written because all ions are canceled out as spectator ions. Therefore, no precipitation reaction occurs
Equilibrium and non-Equilibrium Conditions
The ion product (Q) of a salt is the product of the concentrations of the ions in solution raised to the same powers as in the solubility product expression. It is analogous to the reaction quotient (Q) discussed for gaseous equilibria. Whereas Ksp describes equilibrium concentrations, the ion product describes concentrations that are not necessarily equilibrium concentrations. An ion product can in principle have any positive value, depending on the concentrations of the ions involved. Only in the special case when its value is identical with Ks does it become the solubility product. A solution in which this is the case is said to be saturated. Thus when
\[[\ce{Ag^{+}}]^2 [\ce{CrO4^{2-}}] = 2.76 \times 10^{-12}\]
at the temperature and pressure at which this value \(K_{sp}\) of applies, we say that the "solution is saturated in silver chromate".
The ion product \(Q\) is analogous to the reaction quotient \(Q\) for gaseous equilibria.
As summarized in Figure \(\PageIndex{3}\), there are three possible conditions for an aqueous solution of an ionic solid:
- \(Q < K_{sp}\). The solution is unsaturated, and more of the ionic solid, if available, will dissolve.
- \(Q = K_{sp}\). The solution is saturated and at equilibrium.
- \(Q > K_{sp}\). The solution is supersaturated, and ionic solid will precipitate.
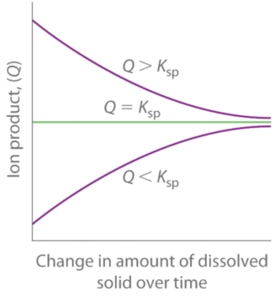
The process of calculating the value of the ion product and comparing it with the magnitude of the solubility product is a straightforward way to determine whether a solution is unsaturated, saturated, or supersaturated. More important, the ion product tells chemists whether a precipitate will form when solutions of two soluble salts are mixed.
Barium sulfate is used in medical imaging of the gastrointestinal tract. Its solubility product is \(1.08 \times 10^{−10}\) at 25°C, so it is ideally suited for this purpose because of its low solubility when a “barium milkshake” is consumed by a patient. The pathway of the sparingly soluble salt can be easily monitored by x-rays. Will barium sulfate precipitate if 10.0 mL of 0.0020 M Na2SO4 is added to 100 mL of 3.2 × 10−4 M BaCl2? Recall that \(\ce{NaCl}\) is highly soluble in water.
Given: Ksp and volumes and concentrations of reactants
Asked for: whether precipitate will form
Strategy:
- Write the balanced equilibrium equation for the precipitation reaction and the expression for Ksp.
- Determine the concentrations of all ions in solution when the solutions are mixed and use them to calculate the ion product (Q).
- Compare the values of Q and Ksp to decide whether a precipitate will form.
Solution
A The only slightly soluble salt that can be formed when these two solutions are mixed is \(\ce{BaSO4}\) because \(\ce{NaCl}\) is highly soluble. The equation for the precipitation of \(\ce{BaSO4}\) is as follows:
\[\ce{BaSO4(s) <=> Ba^{2+} (aq) + SO^{2−}4(aq)} \nonumber\]
The solubility product expression is as follows:
B To solve this problem, we must first calculate the ion product:
\[Q = [\ce{Ba^{2+}}][\ce{SO4^{2−}}] \nonumber\]
using the concentrations of the ions that are present after the solutions are mixed and before any reaction occurs. The concentration of Ba2+ when the solutions are mixed is the total number of moles of Ba2+ in the original 100 mL of \(\ce{BaCl2}\) solution divided by the final volume (100 mL + 10.0 mL = 110 mL):
\[ \begin{align*} \textrm{moles Ba}^{2+}=\textrm{100 mL}\left(\dfrac{\textrm{1 L}}{\textrm{1000 mL}}\right)\left(\dfrac{3.2\times10^{-4}\textrm{ mol}}{\textrm{1 L}} \right )=3.2\times10^{-5}\textrm{ mol Ba}^{2+} \\[4pt] [\mathrm{Ba^{2+}}]=\left(\dfrac{3.2\times10^{-5}\textrm{ mol Ba}^{2+}}{\textrm{110 mL}}\right)\left(\dfrac{\textrm{1000 mL}}{\textrm{1 L}}\right)=2.9\times10^{-4}\textrm{ M Ba}^{2+} \end{align*}\]
Similarly, the concentration of SO42− after mixing is the total number of moles of SO42− in the original 10.0 mL of Na2SO4 solution divided by the final volume (110 mL):
\[ \begin{align*} \textrm{moles SO}_4^{2-} &=\textrm{10.0 mL}\left(\dfrac{\textrm{1 L}}{\textrm{1000 mL}}\right)\left(\dfrac{\textrm{0.0020 mol}}{\textrm{1 L}}\right)=2.0\times10^{-5}\textrm{ mol SO}_4^{2-} \\[4pt] [\mathrm{SO_4^{2-}}] &=\left(\dfrac{2.0\times10^{-5}\textrm{ mol SO}_4^{2-}}{\textrm{110 mL}} \right )\left(\dfrac{\textrm{1000 mL}}{\textrm{1 L}}\right)=1.8\times10^{-4}\textrm{ M SO}_4^{2-} \end{align*}\]
We can now calculate \(Q\):
C We now compare \(Q\) with the \(K_{sp}\). If Q > Ksp, then \(\ce{BaSO4}\) will precipitate, but if Q < Ksp, it will not. Because Q > Ksp, we predict that \(\ce{BaSO4}\) will precipitate when the two solutions are mixed. In fact, \(\ce{BaSO4}\) will continue to precipitate until the system reaches equilibrium, which occurs when
\[[\ce{Ba^{2+}}][\ce{SO4^{2−}}] = K_{sp} = 1.08 \times 10^{−10}. \nonumber\]
The solubility product of calcium fluoride (\(\ce{CaF2}\)) is \(3.45 \times 10^{−11}\). If 2.0 mL of a 0.10 M solution of \(\ce{NaF}\) is added to 128 mL of a \(2.0 \times 10^{−5}\,M\) solution of \(\ce{Ca(NO3)2}\), will \(\ce{CaF2}\) precipitate?
- Answer
-
Yes, since \(Q_{sp} = 4.7 \times 10^{−11} > K_{sp}\).
A solution must be saturated to be in equilibrium with the solid. This is a necessary condition for solubility equilibrium, but it is not by itself sufficient. True chemical equilibrium can only occur when all components are simultaneously present. A solubility system can be in equilibrium only when some of the solid is in contact with a saturated solution of its ions. Failure to appreciate this is a very common cause of errors in solving solubility problems.
If the ion product is smaller than the solubility product, the system is not in equilibrium and no solid can be present. Such a solution is said to be undersaturated. A supersaturated solution is one in which the ion product exceeds the solubility product. A supersaturated solution is not at equilibrium, and no solid can ordinarily be present in such a solution. If some of the solid is added, the excess ions precipitate out and until solubility equilibrium is achieved.
How to know the saturation status of a solution? Just comparing the ion product Qs with the solubility product Ksp. as shown in Table \(\PageIndex{1}\).
| \(Q_{sp}/K_{sp}\) | Status |
|---|---|
| > 1 | Product concentration too high for equilibrium; net reaction proceeds to left. |
| = 1 | System is at equilibrium; no net change will occur. |
| < 1 | Product concentration too low for equilibrium; net reaction proceeds to right. |
For example, for the system
\[\ce{Ag2CrO4(s) <=> 2 Ag^{+} + CrO_4^{2–}} \label{4ba}\]
a solution in which Qs < Ks (i.e., Ks /Qs > 1) is undersaturated (blue shading) and the no solid will be present. The combinations of [Ag+] and [CrO42–] that correspond to a saturated solution (and thus to equilibrium) are limited to those described by the curved line. The pink area to the right of this curve represents a supersaturated solution.

For some substances, formation of a solid or crystallization does not occur automatically whenever a solution is saturated. These substances have a tendency to form oversaturated solutions. For example, syrup and honey are oversaturated sugar solutions, containing other substances such as citric acids. For oversatureated solutions, Qsp is greater than Ksp. When a seed crystal is provided or formed, a precipitate will form immediately due to equilibrium of requiring \(Q_{sp}\) to approach \(K_{sp}\). For example Sodium acetate trihydrate, \(\ce{NaCH3COO\cdot 3H2O}\), when heated to 370 K will become a liquid and stays as a liquid when cooled to room temperature or even below 273 K (Video \(\PageIndex{1}\)). As soon as a seed crystal is present, crystallization occurs rapidly. In such a process, heat is released since this is an exothermic process \(\Delta H < 0\).
Video \(\PageIndex{1}\): "hot ice" (sodium acetate) crystallized from a non-equilibrium supersaturated (\(Q_{sp} > K_{sp}\)) solution
A sample of groundwater that has percolated through a layer of gypsum (\(\ce{CaSO4}\)) with \(K_{sp} = 4.9 \times 10^{–5} = 10^{–4.3}\)) is found to have be \(8.4 \times 10^{–5}\; M\) in Ca2+ and \(7.2 \times 10^{–5}\; M\) in SO42–. What is the equilibrium state of this solution with respect to gypsum?
Solution
The ion product
\[Q_s = (8.4 \times 10^{–5})(7.2 \times 10^{-5}) = 6.0 \times 10^{–4} \nonumber\]
exceeds \(K_{sp}\), so the ratio \(K_{sp} /Q_{sp} > 1\) and the solution is supersaturated in \(\ce{CaSO_4}\).
Relating Solubilities to Solubility Constants
The solubility (by which we usually mean the molar solubility) of a solid is expressed as the concentration of the "dissolved solid" in a saturated solution. In the case of a simple 1:1 solid such as AgCl, this would just be the concentration of Ag+ or Cl– in the saturated solution. But for a more complicated stoichiometry such as as silver chromate, the solubility would be only one-half of the Ag+ concentration.
For example, let us denote the solubility of Ag2CrO4 as S mol L–1. Then for a saturated solution, we have
- \([Ag^+] = 2S\)
- \( [CrO_4^{2–}] = S\)
Substituting this into Eq 5b above,
\[(2S)^2 (S) = 4S^3 = 2.76 \times 10^{–12}\]
\[S= \left( \dfrac{K_{sp}}{4} \right)^{1/3} = (6.9 \times 10^{-13})^{1/3} = 0.88 \times 10^{-4} \label{6a}\]
thus the solubility is \(8.8 \times 10^{–5}\; M\).
Note that the relation between the solubility and the solubility product constant depends on the stoichiometry of the dissolution reaction. For this reason it is meaningless to compare the solubilities of two salts having the formulas A2B and AB2, say, on the basis of their Ks values.
It is meaningless to compare the solubilities of two salts having different formulas on the basis of their Ks values.
The solubility of CaF2 (molar mass 78.1) at 18°C is reported to be 1.6 mg per 100 mL of water. Calculate the value of Ks under these conditions.
Solution
moles of solute in 100 mL; S = 0.0016 g / 78.1 g/mol = \(2.05 \times 10^{-5}\) mol
\[S = \dfrac{2.05 \times 10^{ –5} mol}{0.100\; L} = 2.05 \times 10^{-4} M\]
\[K_{sp}= [Ca^{2+}][F^–]^2 = (S)(2S)^2 = 4 × (2.05 \times 10^{–4})^3 = 3.44 \times 10^{–11}\]
Estimate the solubility of La(IO3)3 and calculate the concentration of iodate in equilibrium with solid lanthanum iodate, for which Ks = 6.2 × 10–12.
Solution
The equation for the dissolution is
\[La(IO_3)_3 \rightleftharpoons La^{3+ }+ 3 IO_3^–\]
If the solubility is S, then the equilibrium concentrations of the ions will be
[La3+] = S and [IO3–] = 3S. Then Ks = [La3+][IO3–]3 = S(3S)3 = 27S4
27S4 = 6.2 × 10–12, S = ( ( 6.2 ÷ 27) × 10–12 )¼ = 6.92 × 10–4 M
[IO3–] = 3S = 2.08 × 10–5 (M)
Cadmium is a highly toxic environmental pollutant that enters wastewaters associated with zinc smelting (Cd and Zn commonly occur together in ZnS ores) and in some electroplating processes. One way of controlling cadmium in effluent streams is to add sodium hydroxide, which precipitates insoluble Cd(OH)2 (Ks = 2.5E–14). If 1000 L of a certain wastewater contains Cd2+ at a concentration of 1.6E–5 M, what concentration of Cd2+ would remain after addition of 10 L of 4 M NaOH solution?
Solution
As with most real-world problems, this is best approached as a series of smaller problems, making simplifying approximations as appropriate.
Volume of treated water: 1000 L + 10 L = 1010 L
Concentration of OH– on addition to 1000 L of pure water:
(4 M) × (10 L)/(1010 L) = 0.040 M
Initial concentration of Cd2+ in 1010 L of water:
\[(1.6 \times 10^{–5}\; M) \left( \dfrac{100}{101} \right) \approx 1.6 \times 10^{–5}\; M\]
The easiest way to tackle this is to start by assuming that a stoichiometric quantity of Cd(OH)2 is formed — that is, all of the Cd2+ gets precipitated.
| Concentrations | \([\ce{Cd^{2+}}],\, M\) | \([\ce{OH^{–}}],\, M\) |
|---|---|---|
| initial | 1.6E–5 | 0.04 |
| change | –1.6E–5 | –3.2E–5 |
| final: | 0 | 0.04 – 3.2E–5 ≈ .04 |
Now "turn on the equilibrium" — find the concentration of Cd2+ that can exist in a 0.04M OH– solution:
| Concentrations | \([\ce{Cd^{2+}}],\, M\) | \([\ce{OH^{–}}],\, M\) |
|---|---|---|
| initial | o | 0.04 |
| change | +x | +2x |
| at equilibrium | x | .04 + 2x ≈ .04 |
Substitute these values into the solubility product expression:
Cd(OH)2(s) = [Cd2+] [OH–]2 = 2.5E–14
[Cd2+] = (2.5E–14) / (16E–4) = 1.6E–13 M
Note that the effluent will now be very alkaline:
\[pH = 14 + \log 0.04 = 12.6\]
so in order to meet environmental standards an equivalent quantity of strong acid must be added to neutralize the water before it is released.
The Common Ion Effect
It has long been known that the solubility of a sparingly soluble ionic substance is markedly decreased in a solution of another ionic compound when the two substances have an ion in common. This is just what would be expected on the basis of the Le Chatelier Principle; whenever the process
\[CaF_{2(s)} \rightleftharpoons Ca^{2+} + 2 F^– \label{7}\]
is in equilibrium, addition of more fluoride ion (in the form of highly soluble NaF) will shift the composition to the left, reducing the concentration of Ca2+, and thus effectively reducing the solubility of the solid. We can express this quantitatively by noting that the solubility product expression
\[[Ca^{2+}][F^–]^2 = 1.7 \times 10^{–10} \label{8}\]
must always hold, even if some of the ionic species involved come from sources other than CaF2(s). For example, if some quantity x of fluoride ion is added to a solution initially in equilibrium with solid CaF2, we have
- \([Ca^{2+}] = S\)
- \([F^–] = 2S + x\)
so that
\[K_{sp} = [Ca^{2+}][ F^–]^2 = S (2S + x)^2 . \label{9a}\]
\[K_{sp} ≈ S x^2 \]
\[S = \dfrac{K_{sp}}{x^2} \label{9b}\]
The plots shown below illustrate the common ion effect for silver chromate as the chromate ion concentration is increased by addition of a soluble chromate such as Na2CrO4.
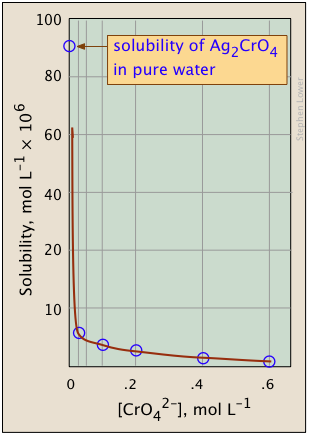
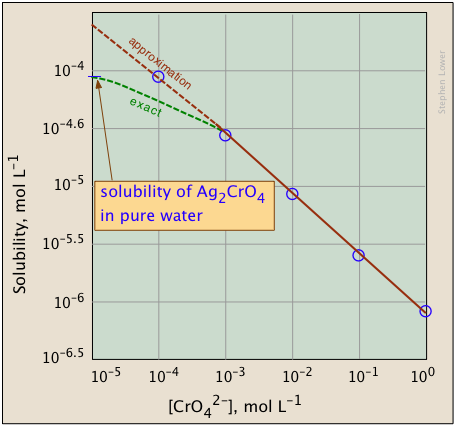
What's different about the plot on the right? If you look carefully at the scales, you will see that this one is plotted logarithmically (that is, in powers of 10.) Notice how a much wider a range of values can display on a logarithmic plot. The point of showing this pair of plots is to illustrate the great utility of log-concentration plots in equilibrium calculations in which simple approximations (such as that made in Equation \(\ref{9b}\)) can yield straight-lines within the range of values for which the approximation is valid.
Calculate the solubility of strontium sulfate (Ks = 2.8 × 10–7) in
- pure water and
- in a 0.10 mol L–1 solution of Na2SO4.
Solution:
(a) In pure water, Ks = [Sr2+][SO42–] = S2
S = √Ks = (2.8 × 10–7)½ = 5.3 × 10–4
(b) In 0.10 mol L–1 Na2SO4, we have
Ks = [Sr2+][SO42–] = S × (0.10 + S) = 2.8 × 10–7
Because S is negligible compared to 0.10 M, we make the approximation
Ks = [Sr2+][SO42–] ≈ S × (0.10 M) = 2.8 × 10–7
so S ≈ (2.8 × 10–7) / 0.10M = 2.8 × 10–6 M — which is roughly 100 times smaller than the result from (a).
The common ion effect usually decreases the solubility of a sparingly soluble salt.
Calculate the solubility of calcium phosphate [Ca3(PO4)2] in 0.20 M CaCl2.
Given: concentration of CaCl2 solution
Asked for: solubility of Ca3(PO4)2 in CaCl2 solution
Strategy:
- Write the balanced equilibrium equation for the dissolution of Ca3(PO4)2. Tabulate the concentrations of all species produced in solution.
- Substitute the appropriate values into the expression for the solubility product and calculate the solubility of Ca3(PO4)2.
Solution
A The balanced equilibrium equation is given in the following table. If we let x equal the solubility of Ca3(PO4)2 in moles per liter, then the change in [Ca2+] is once again +3x, and the change in [PO43−] is +2x. We can insert these values into the ICE table.
\[Ca_3(PO_4)_{2(s)} \rightleftharpoons 3Ca^{2+} (aq) + 2PO^{3−}_{4(aq)}\]
| \(\ce{Ca3(PO4)2}\) | \(\ce{[Ca2+]}\) | \(\ce{[PO43−]}\) | |
|---|---|---|---|
| initial | pure solid | 0.20 | 0 |
| change | — | +3x | +2x |
| final | pure solid | 0.20 + 3x | 2x |
B The Ksp expression is as follows:
Because Ca3(PO4)2 is a sparingly soluble salt, we can reasonably expect that x << 0.20. Thus (0.20 + 3x) M is approximately 0.20 M, which simplifies the Ksp expression as follows:
\\x^2&=6.5\times10^{-32}
\\x&=2.5\times10^{-16}\textrm{ M}\end{align}\]
This value is the solubility of Ca3(PO4)2 in 0.20 M CaCl2 at 25°C. It is approximately nine orders of magnitude less than its solubility in pure water, as we would expect based on Le Chatelier’s principle. With one exception, this example is identical to Example \(\PageIndex{2}\)—here the initial [Ca2+] was 0.20 M rather than 0.
Calculate the solubility of silver carbonate in a 0.25 M solution of sodium carbonate. The solubility of silver carbonate in pure water is 8.45 × 10−12 at 25°C.
- Answer
-
2.9 × 10−6 M (versus 1.3 × 10−4 M in pure water)
Applications and Examples
Precipitation reactions are useful in determining whether a certain element is present in a solution. If a precipitate is formed when a chemical reacts with lead, for example, the presence of lead in water sources could be tested by adding the chemical and monitoring for precipitate formation. In addition, precipitation reactions can be used to extract elements, such as magnesium from seawater. Precipitation reactions even occur in the human body between antibodies and antigens; however, the environment in which this occurs is still being studied.
Complete the double replacement reaction and then reduce it to the net ionic equation.
\[NaOH (aq) + MgCl_{2 \;(aq)} \rightarrow \nonumber \]
First, predict the products of this reaction using knowledge of double replacement reactions (remember the cations and anions “switch partners”).
\[2NaOH (aq) + MgCl_{2\;(aq)} \rightarrow 2NaCl + Mg(OH)_2 \nonumber\]
Second, consult the solubility rules to determine if the products are soluble. Group 1 cations (\(Na^+\)) and chlorides are soluble from rules 1 and 3 respectively, so \(NaCl\) will be soluble in water. However, rule 6 states that hydroxides are insoluble, and thus \(Mg(OH)_2\) will form a precipitate. The resulting equation is the following:
\[2NaOH(aq) + MgCl_{2\;(aq)} \rightarrow 2NaCl (aq) + Mg(OH)_{2\;(s)} \nonumber\]
Third, separate the reactants into their ionic forms, as they would exist in an aqueous solution. Be sure to balance both the electrical charge and the number of atoms:
\[2Na^+ (aq) + 2OH^- (aq) + Mg^{2+} (aq) + 2Cl^- (aq) \rightarrow Mg(OH)_{2\;(s)} + 2Na^+ (aq) + 2Cl^- (aq) \nonumber\]
Lastly, eliminate the spectator ions (the ions that occur on both sides of the equation unchanged). In this case, they are the sodium and chlorine ions. The final net ionic equation is:
\[Mg^{2+} (aq) + 2OH^- (aq) \rightarrow Mg(OH)_{2(s)} \nonumber\]
Complete the double replacement reaction and then reduce it to the net ionic equation.
\[CoCl_{2\;(aq)} + Na_2SO_{4\;(aq)} \rightarrow \nonumber\]
Solution
The predicted products of this reaction are \(CoSO_4\) and \(NaCl\). From the solubility rules, \(CoSO_4\) is soluble because rule 4 states that sulfates (\(SO_4^{2-}\)) are soluble. Similarly, we find that \(NaCl\) is soluble based on rules 1 and 3. After balancing, the resulting equation is as follows:
\[CoCl_{2\;(aq)} + Na_2SO_{4\;(aq)} \rightarrow CoSO_{4\;(aq)} + 2 NaCl (aq) \nonumber\]
Separate the species into their ionic forms, as they would exist in an aqueous solution. Balance the charge and the atoms. Cancel out all spectator ions (those that appear as ions on both sides of the equation.):
Co2- (aq) + 2Cl-(aq) + 2Na+ (aq) + SO42-(aq) → Co2- (aq) + SO42-(aq) + 2Na+ (aq) + 2Cl-(aq)
No precipitation reaction
This particular example is important because all of the reactants and the products are aqueous, meaning they cancel out of the net ionic equation. There is no solid precipitate formed; therefore, no precipitation reaction occurs.
Write the net ionic equation for the potentially double displacement reactions. Make sure to include the states of matter and balance the equations.
- \(Fe(NO_3)_{3\;(aq)} + NaOH (aq) \rightarrow\)
- \(Al_2(SO_4)_{3\;(aq)} + BaCl_{2\;(aq)} \rightarrow\)
- \(HI (aq) + Zn(NO_3)_{2\;(aq)} \rightarrow\)
- \(CaCl_{2\;(aq)} + Na_3PO_{4\;(aq)} \rightarrow\)
- \(Pb(NO_3)_{2\;(aq)} + K_2SO_{4 \;(aq)} \rightarrow\)
Solutions
a. Regardless of physical state, the products of this reaction are \(Fe(OH)_3\) and \(NaNO_3\). The solubility rules predict that \(NaNO_3\) is soluble because all nitrates are soluble (rule 2). However, \(Fe(OH)_3\) is insoluble, because hydroxides are insoluble (rule 6) and \(Fe\) is not one of the cations which results in an exception. After dissociation, the ionic equation is as follows:
\[Fe^{3+} (aq) + NO^-_{3\;(aq)} + Na^+ (aq) + 3OH^- (aq) \rightarrow Fe(OH)_{3\;(s)} + Na^+ (aq) + NO^-_{3\;(aq)} \nonumber\]
Canceling out spectator ions leaves the net ionic equation:
\[Fe^{3+} (aq) + OH^- (aq) \rightarrow Fe(OH)_{\;3(s)} \nonumber\]
b. From the double replacement reaction, the products are \(AlCl_3\) and \(BaSO_4\). \(AlCl_3\) is soluble because it contains a chloride (rule 3); however, \(BaSO_4\) is insoluble: it contains a sulfate, but the \(Ba^{2+}\) ion causes it to be insoluble because it is one of the cations that causes an exception to rule 4. The ionic equation is (after balancing):
\[2Al^{3+} (aq) + 6Cl^- (aq) + 3Ba^{2+} (aq) + 3SO^{2-}_{4\;(aq)} \rightarrow 2 Al^{3+} (aq) +6Cl^- (aq) + 3BaSO_{4\;(s)} \nonumber\]
Canceling out spectator ions leaves the following net ionic equation:
\[Ba^{2+} (aq) + SO^{2-}_{4\;(aq)} \rightarrow BaSO_{4\;(s)} \nonumber\]
c. From the double replacement reaction, the products \(HNO_3\) and \(ZnI_2\) are formed. Looking at the solubility rules, \(HNO_3\) is soluble because it contains nitrate (rule 2), and \(ZnI_2\) is soluble because iodides are soluble (rule 3). This means that both the products are aqueous (i.e. dissociate in water), and thus no precipitation reaction occurs.
d. The products of this double replacement reaction are \(Ca_3(PO_4)_2\) and \(NaCl\). Rule 1 states that \(NaCl\) is soluble, and according to solubility rule 6, \(Ca_3(PO_4)_2\) is insoluble. The ionic equation is:
\[Ca^{2+} (aq) + Cl^- (aq) + Na^+ (aq) + PO^{3-}_{4\;(aq)} \rightarrow Ca_3(PO_4)_{2\;(s)} + Na^+ (aq) + Cl^- (aq) \nonumber \]
After canceling out spectator ions, the net ionic equation is given below:
\[Ca^{2+} (aq) + PO^{3-}_{4\;(aq)} \rightarrow Ca_3(PO_4)_{2\;(s)} \nonumber\]
e. The first product of this reaction, \(PbSO_4\), is soluble according to rule 4 because it is a sulfate. The second product, \(KNO_3\), is also soluble because it contains nitrate (rule 2). Therefore, no precipitation reaction occurs.
References
- Campbell, Dan, Linus Pauling, and Davis Pressman. "The Nature of the Forces Between Antigen and Antibody and of the Precipitation Reaction." Physiological Reviews 23.3 (1943): 203-219. Online.
- Harwood, William, F Herring, Jeffry Madura, and Ralph Petrucci. General Chemistry. 9th ed. Upper Saddle River: Pearson Pretence Hall, 2007. Print.
- Freeouf, J.L, Grischkowsky, D., McInturff, D.T., Warren, A.C., & Woodall, J.M. (1990). Arsenic precipitates and the semi-insulating properties of gaas buffer layers grown by low-temperature molecular beam epitaxy. Applied Physics Letters, 57(13)
- Petrucci, et al. General Chemistry: Principles & Modern Applications. 9th ed. Upper Saddle River, New Jersey 2007.
Summary
In contrast to \(K_{sp}\), the ion product (\(Q_{sp}\)) describes concentrations that are not necessarily equilibrium concentrations. Comparing Q and Ksp enables us to determine whether a precipitate will form when solutions of two soluble salts are mixed. Adding a common cation or common anion to a solution of a sparingly soluble salt shifts the solubility equilibrium in the direction predicted by Le Chatelier’s principle. The solubility of the salt is almost always decreased by the presence of a common ion.
Contributors and Attributions
- Julie Schaffer (UCD), Corinne Herman (UCD)
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

