16.1: The Nature of Solubility Equilibria
- Page ID
- 41630
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Understand the qualitative nature of dissolving a salt in water
Dissolution of a salt in water is a chemical process that is governed by the same laws of chemical equilibrium that apply to any other reaction. There are, however, a number of special aspects of of these equilibria that set them somewhat apart from the more general ones that are covered in the lesson set devoted specifically to chemical equilibrium. These include such topics as the common ion effect, the influence of pH on solubility, supersaturation, and some special characteristics of particularly important solubility systems... all explained in what follows.
The Dissolution of Salts in Water
Drop some ordinary table salt into a glass of water, and watch it "disappear". We refer to this as dissolution, and we explain it as a process in which the sodium and chlorine units break away from the crystal surface, get surrounded by H2O molecules, and become hydrated ions.
\[\ce{NaCl_(s) \rightarrow Na^{+}(aq) + Cl^{–}(aq)} \nonumber\]
The designation (aq) means "aqueous" and comes from aqua, the Latin word for water. It is used whenever we want to emphasize that the ions are hydrated — that H2O molecules are attached to them.
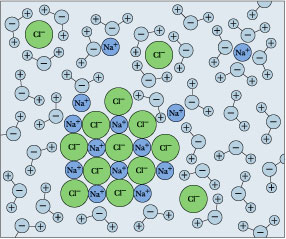
Remember that solubility equilibrium and the calculations that relate to it are only meaningful when both sides (solids and dissolved ions) are simultaneously present. But if you keep adding salt, there will come a point at which it no longer seems to dissolve. If this condition persists, we say that the salt has reached its solubility limit, and the solution is saturated in NaCl. The situation is now described by
\[\ce{NaCl_(s) <=>Na^{+}(aq) + Cl^{–}(aq)} \nonumber\]
in which the solid and its ions are in equilibrium.
Salt solutions that have reached or exceeded their solubility limits (usually 36-39 g per 100 mL of water) are responsible for prominent features of the earth's geochemistry. They typically form when NaCl leaches from soils into waters that flow into salt lakes in arid regions that have no natural outlets; subsequent evaporation of these brines force the above equilibrium to the left, forming natural salt deposits. These are often admixed with other salts, but in some cases are almost pure NaCl. Many parts of the world contain buried deposits of NaCl (known as halite) that formed from the evaporation of ancient seas, and which are now mined.
Expressing solubilities
Solubilities are most fundamentally expressed in molar (mol L–1 of solution) or molal (mol kg–1 of water) units. But for practical use in preparing stock solutions, chemistry handbooks usually express solubilities in terms of grams-per-100 ml of water at a given temperature, frequently noting the latter in a superscript. Thus 6.9 20 means 6.9 g of solute will dissolve in 100 mL of water at 20° C.
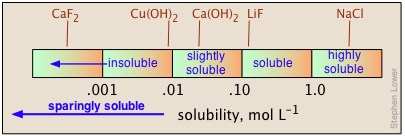
When quantitative data are lacking, the designations "soluble", "insoluble", "slightly soluble", and "highly soluble" are used. There is no agreed-on standard for these classifications, but a useful guideline might be that shown below.
What determines solubility?
The solubilities of salts in water span a remarkably large range of values, from almost completely insoluble to highly soluble. Moreover, there is no simple way of predicting these values, or even of explaining the trends that are observed for the solubilities of different anions within a given group of the periodic table.

Ultimately, the driving force for dissolution (and for all chemical processes) is determined by the Gibbs free energy change. Dissolution of a salt is conceptually understood as a sequence of the two processes depicted above:
- breakup of the ionic lattice of the solid (i.e., lattice energy)
- followed by attachment of water molecules to the released ions (Solvation or Hydration Energy).
The first step consumes a large quantity of energy, something that by itself would strongly discourage solubility. But the second step releases a large amount of energy and thus has the opposite effect. Thus the net energy change depends on the sum of two large energy terms (often approaching 1000 kJ/mol) having opposite signs. Each of these terms will to some extent be influenced by the size, charge, and polarizability of the particular ions involved, and on the lattice structure of the solid. This large number of variables makes it impossible to predict the solubility of a given salt.
Nevertheless, there are some clear trends for how the solubilities of a series of salts of a given anion (such as hydroxides, sulfates, etc.) change with a periodic table group. And of course, there are a number of general solubility rules.
- Salts containing Group I elements are soluble (Li+, Na+, K+, Cs+, Rb+). Exceptions to this rule are rare. Salts containing the ammonium ion (NH4+) are also soluble.
- Salts containing nitrate ion (NO3-) are generally soluble.
- Salts containing Cl -, Br -, I - are generally soluble. Important exceptions to this rule are halide salts of Ag+, Pb2+, and (Hg2)2+. Thus, AgCl, PbBr2, and Hg2Cl2 are all insoluble.
- Most silver salts are insoluble. AgNO3 and Ag(C2H3O2) are common soluble salts of silver; virtually anything else is insoluble.
- Most sulfate salts are soluble. Important exceptions to this rule include BaSO4, PbSO4, Ag2SO4 and SrSO4 .
- Most hydroxide salts are only slightly soluble. Hydroxide salts of Group I elements are soluble. Hydroxide salts of Group II elements (Ca, Sr, and Ba) are slightly soluble. Hydroxide salts of transition metals and Al3+ are insoluble. Thus, Fe(OH)3, Al(OH)3, Co(OH)2 are not soluble.
- Most sulfides of transition metals are highly insoluble. Thus, CdS, FeS, ZnS, Ag2S are all insoluble. Arsenic, antimony, bismuth, and lead sulfides are also insoluble.
- Carbonates are frequently insoluble. Group II carbonates (Ca, Sr, and Ba) are insoluble. Some other insoluble carbonates include FeCO3 and PbCO3.
- Chromates are frequently insoluble. Examples: PbCrO4, BaCrO4
- Phosphates are frequently insoluble. Examples: Ca3(PO4)2, Ag3PO4
- Fluorides are frequently insoluble. Examples: BaF2, MgF2 PbF2.
A solution must be saturated to be in equilibrium with the solid. This is a necessary condition for solubility equilibrium, but it is not by itself sufficient. True chemical equilibrium can only occur when all components are simultaneously present. A solubility system can be in equilibrium only when some of the solid is in contact with a saturated solution of its ions. Failure to appreciate this is a very common cause of errors in solving solubility problems.
If the ion product is smaller than the solubility product, the system is not in equilibrium and no solid can be present. Such a solution is said to be undersaturated. A supersaturated solution is one in which the ion product exceeds the solubility product. A supersaturated solution is not at equilibrium, and no solid can ordinarily be present in such a solution. If some of the solid is added, the excess ions precipitate out and until solubility equilibrium is achieved.
Solubility and Temperature
Solubility usually increases with temperature - but not always. This is very apparent from the solubility-vs.-temperature plots shown in Figure \(\PageIndex{1}\). (Some of the plots are colored differently in order to make it easier to distinguish them where they crowd together.) The temperature dependence of any process depends on its entropy change — that is, on the degree to which thermal kinetic energy can spread throughout the system. When a solid dissolves, its component molecules or ions diffuse into the much greater volume of the solution, carrying their thermal energy along with them. So we would normally expect the entropy to increase — something that makes any process take place to a greater extent at a higher temperature.
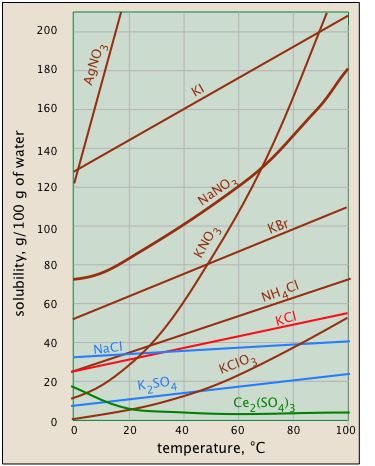
So why does the solubility of cerium sulfate (green plot) diminish with temperature? Dispersal of the Ce3+ and SO42– ions themselves is still associated with an entropy increase, but in this case the entropy of the waterdecreases even more owing to the ordering of the H2O molecules that attach to the Ce3+ ions as they become hydrated. It's difficult to predict these effects, or explain why they occur in individual cases — but they do happen.
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook


