13.2: Entropy and Spontaneity - A Molecular Statistical Interpretation
- Page ID
- 41607
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- The Learning Objective of this Module is to understand the relationship between internal energy and entropy.
We know that the first law of thermodynamics governs changes in the state function we called internal energy (\(U\)) and that changes in the internal energy (\(ΔU\)) are closely related to changes in the enthalpy (\(ΔH\)), which is a measure of the heat flow between a system and its surroundings at constant pressure. You also learned previously that the enthalpy change for a chemical reaction can be calculated using tabulated values of enthalpies of formation. This information, however, does not tell us whether a particular process or reaction will occur spontaneously.
Spontaneous Reactions
Let’s consider a familiar example of spontaneous change. If a hot frying pan that has just been removed from the stove is allowed to come into contact with a cooler object, such as cold water in a sink, heat will flow from the hotter object to the cooler one, in this case usually releasing steam. Eventually both objects will reach the same temperature, at a value between the initial temperatures of the two objects. This transfer of heat from a hot object to a cooler one obeys the first law of thermodynamics: energy is conserved.
Now consider the same process in reverse. Suppose that a hot frying pan in a sink of cold water were to become hotter while the water became cooler. As long as the same amount of thermal energy was gained by the frying pan and lost by the water, the first law of thermodynamics would be satisfied. Yet we all know that such a process cannot occur: heat always flows from a hot object to a cold one, never in the reverse direction. That is, by itself the magnitude of the heat flow associated with a process does not predict whether the process will occur spontaneously.
For many years, chemists and physicists tried to identify a single measurable quantity that would enable them to predict whether a particular process or reaction would occur spontaneously. Initially, many of them focused on enthalpy changes and hypothesized that an exothermic process would always be spontaneous. But although it is true that many, if not most, spontaneous processes are exothermic, there are also many spontaneous processes that are not exothermic. For example, at a pressure of 1 atm, ice melts spontaneously at temperatures greater than 0°C, yet this is an endothermic process because heat is absorbed. Similarly, many salts (such as NH4NO3, NaCl, and KBr) dissolve spontaneously in water even though they absorb heat from the surroundings as they dissolve (i.e., \(ΔH_{soln} > 0\)). Reactions can also be both spontaneous and highly endothermic, like the reaction of barium hydroxide with ammonium thiocyanate shown in Figure \(\PageIndex{1}\).
Thus enthalpy is not the only factor that determines whether a process is spontaneous. For example, after a cube of sugar has dissolved in a glass of water so that the sucrose molecules are uniformly dispersed in a dilute solution, they never spontaneously come back together in solution to form a sugar cube. Moreover, the molecules of a gas remain evenly distributed throughout the entire volume of a glass bulb and never spontaneously assemble in only one portion of the available volume. To help explain why these phenomena proceed spontaneously in only one direction requires an additional state function called entropy (\(S\)), a thermodynamic property of all substances that is proportional to their degree of disorder.
The direction of a spontaneous process is not governed by the internal energy change nor enthalpy change and thus the First Law of Thermodynamics cannot predict the direction of a natural process
Probabilities and Microstates
Chemical and physical changes in a system may be accompanied by either an increase or a decrease in the disorder of the system, corresponding to an increase in entropy (\(ΔS > 0\)) or a decrease in entropy (\(ΔS < 0\)), respectively. As with any other state function, the change in entropy is defined as the difference between the entropies of the final and initial states:
\[ΔS = S_f − S_i\]
When a gas expands into a vacuum, its entropy increases because the increased volume allows for greater atomic or molecular disorder. The greater the number of atoms or molecules in the gas, the greater the disorder. The magnitude of the entropy of a system depends on the number of microscopic states, or microstates, associated with it (in this case, the number of atoms or molecules); that is, the greater the number of microstates, the greater the entropy.
How can we express disorder quantitatively? From the example of coins, you can probably see that simple statistics plays a role: the probability of obtaining three heads and seven tails after tossing ten coins is just the ratio of the number of ways that ten different coins can be arranged in this way, to the number of all possible arrangements of ten coins.

Using the language of molecular statistics, we say that a collection of coins in which a given fraction of its members are heads-up constitutes a macroscopic state of the system. Since we do not care which coins are heads-up, there are clearly numerous configurations of the individual coins which can result in this “macrostate”. Each of these configurations specifies a microscopic state of the system. The greater the number of microstates that correspond to a given macrostate (or configuration), the greater the probability of that macrostate. To see what this means, consider the possible outcomes of a toss of four coins (Table \(\PageIndex{1}\)):
| macrostate (Configuration) | ways | probability |
microstates
|
|---|---|---|---|
| 0 heads | 1 | 1/16 | TTTT |
| 1 head | 4 | 4/16 = 1/4 | HTTT THTT TTHT TTTH |
| 2 heads | 6 | 6/16 = 3/8 | HHTT HTHT HTTH THHT TTHH THTH |
| 3 heads | 4 | 4/16 = 1/4 | HHHT HTHH HHTH THHH |
| 4 heads | 1 | 1/16 | HHHH |
A toss of four coins will yield one of the five outcomes (macrostates) listed in the leftmost column of the table. The second column gives the number of “ways”— that is, the number of head/tail configurations of the set of coins (the number of microstates)— that can result in the macrostate. The probability of a toss resulting in a particular macrostate is proportional to the number of microstates corresponding to the macrostate, and is equal to this number, divided by the total number of possible microstates (in this example, 24 =16). An important assumption here is that all microstates are equally probable; that is, the toss is a “fair” one in which the many factors that determine the trajectory of each coin operate in an entirely random way.
The greater the number of microstates that correspond to a given macrostate, the greater the probability of that macrostate.
Entropy and Microstates
Following the work of Carnot and Clausius, Ludwig Boltzmann developed a molecular-scale statistical model that related the entropy of a system to the number of microstates possible for the system. A microstate (\(\Omega\)) is a specific configuration of the locations and energies of the atoms or molecules that comprise a system like the following:
\[S=k \ln \Omega \label{Eq2}\]
Here k is the Boltzmann constant and has a value of 1.38 × 10−23 J/K.
As for other state functions, the change in entropy for a process is the difference between its final (\(S_f\)) and initial (\(S_i\)) values:
\[\begin{align} ΔS &= S_\ce{f}−S_\ce{i} \\[4pt] &=k \ln \Omega_\ce{f} − k \ln \Omega_\ce{i} \\[4pt] &= k \ln\dfrac{\Omega_\ce{f}}{\Omega_\ce{i}} \label{Eq2a} \end{align}\]
For processes involving an increase in the number of microstates, \(\Omega_f > \Omega_i\), the entropy of the system increases, \(ΔS > 0\). Conversely, processes that reduce the number of microstates, \(\Omega_f < \Omega_i\), yield a decrease in system entropy, \(ΔS < 0\). This molecular-scale interpretation of entropy provides a link to the probability that a process will occur as illustrated in the next paragraphs.
Consider the general case of a system comprised of N particles distributed among n boxes. The number of microstates possible for such a system is nN. For example, distributing four particles among two boxes will result in 24 = 16 different microstates as illustrated in Figure \(\PageIndex{2}\). Microstates with equivalent particle arrangements (not considering individual particle identities) are grouped together and are called distributions. The probability that a system will exist with its components in a given distribution is proportional to the number of microstates within the distribution. Since entropy increases logarithmically with the number of microstates (Equation \ref{Eq2}), the most probable distribution is therefore the one of greatest entropy.
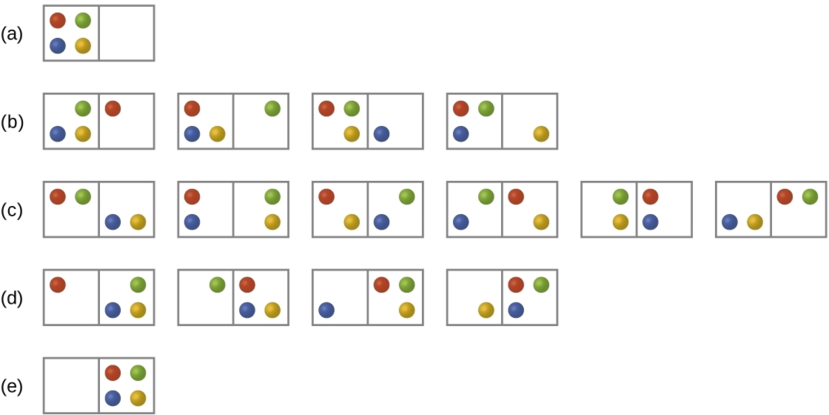
For this system, the most probable configuration is one of the six microstates associated with distribution (c) where the particles are evenly distributed between the boxes, that is, a configuration of two particles in each box. The probability of finding the system in this configuration is
\[\dfrac{6}{16} = \dfrac{3}{8} \nonumber\]
The least probable configuration of the system is one in which all four particles are in one box, corresponding to distributions (a) and (e), each with a probability of
\[\dfrac{1}{16} \nonumber\]
The probability of finding all particles in only one box (either the left box or right box) is then
\[\left(\dfrac{1}{16}+\dfrac{1}{16}\right)=\dfrac{2}{16} = \dfrac{1}{8} \nonumber\]
As you add more particles to the system, the number of possible microstates increases exponentially (2N). A macroscopic (laboratory-sized) system would typically consist of moles of particles (N ~ 1023), and the corresponding number of microstates would be staggeringly huge. Regardless of the number of particles in the system, however, the distributions in which roughly equal numbers of particles are found in each box are always the most probable configurations.
The previous description of an ideal gas expanding into a vacuum is a macroscopic example of this particle-in-a-box model. For this system, the most probable distribution is confirmed to be the one in which the matter is most uniformly dispersed or distributed between the two flasks. The spontaneous process whereby the gas contained initially in one flask expands to fill both flasks equally therefore yields an increase in entropy for the system.
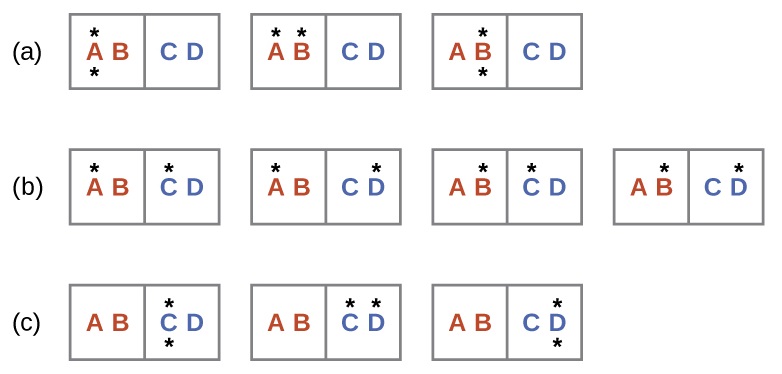
A similar approach may be used to describe the spontaneous flow of heat. Consider a system consisting of two objects, each containing two particles, and two units of energy (represented as “*”) in Figure \(\PageIndex{3}\). The hot object is comprised of particles A and B and initially contains both energy units. The cold object is comprised of particles C and D, which initially has no energy units. Distribution (a) shows the three microstates possible for the initial state of the system, with both units of energy contained within the hot object. If one of the two energy units is transferred, the result is distribution (b) consisting of four microstates. If both energy units are transferred, the result is distribution (c) consisting of three microstates. And so, we may describe this system by a total of ten microstates. The probability that the heat does not flow when the two objects are brought into contact, that is, that the system remains in distribution (a), is \(\frac{3}{10}\). More likely is the flow of heat to yield one of the other two distribution, the combined probability being \(\frac{7}{10}\). The most likely result is the flow of heat to yield the uniform dispersal of energy represented by distribution (b), the probability of this configuration being \(\frac{4}{10}\). As for the previous example of matter dispersal, extrapolating this treatment to macroscopic collections of particles dramatically increases the probability of the uniform distribution relative to the other distributions. This supports the common observation that placing hot and cold objects in contact results in spontaneous heat flow that ultimately equalizes the objects’ temperatures. And, again, this spontaneous process is also characterized by an increase in system entropy.
Consider the system shown here. What is the change in entropy for a process that converts the system from distribution (a) to (c)?

Solution
We are interested in the following change:
The initial number of microstates is one, the final six:
\[\begin{align*} ΔS &=k \ln\dfrac{\Omega_\ce{c}}{\Omega_\ce{a}}\nonumber \\[4pt] &= 1.38×10^{−23}\:J/K × \ln\dfrac{6}{1} \\[4pt] &= 2.47×10^{−23}\:J/K \end{align*} \]
The sign of this result is consistent with expectation; since there are more microstates possible for the final state than for the initial state, the change in entropy should be positive.
Consider the system shown in Figure \(\PageIndex{3}\). What is the change in entropy for the process where all the energy is transferred from the hot object (AB) to the cold object (CD)?
- Answer
-
0 J/K
A disordered system has a greater number of possible microstates than does an ordered system, so it has a higher entropy. This is most clearly seen in the entropy changes that accompany phase transitions, such as solid to liquid or liquid to gas. As you know, a crystalline solid is composed of an ordered array of molecules, ions, or atoms that occupy fixed positions in a lattice, whereas the molecules in a liquid are free to move and tumble within the volume of the liquid; molecules in a gas have even more freedom to move than those in a liquid. Each degree of motion increases the number of available microstates, resulting in a higher entropy. Thus the entropy of a system must increase during melting (ΔSfus > 0). Similarly, when a liquid is converted to a vapor, the greater freedom of motion of the molecules in the gas phase means that ΔSvap > 0. Conversely, the reverse processes (condensing a vapor to form a liquid or freezing a liquid to form a solid) must be accompanied by a decrease in the entropy of the system: ΔS < 0.
Entropy (S) is a thermodynamic property of all substances that is proportional to their degree of disorder. The greater the number of possible microstates for a system, the greater the disorder and the higher the entropy.
Disorder is more probable than order because there are so many more ways of achieving it. Thus coins and cards tend to assume random configurations when tossed or shuffled, and socks and books tend to become more scattered about a teenager’s room during the course of daily living. But there are some important differences between these large-scale mechanical, or macro systems, and the collections of sub-microscopic particles that constitute the stuff of chemistry, and which we will refer to here generically as molecules. Molecules, unlike macro objects, are capable of accepting, storing, and giving up energy in tiny amounts (quanta), and act as highly efficient carriers and spreaders of thermal energy as they move around. Thus, in chemical systems,
- We are dealing with huge numbers of particles. This is important because statistical predictions are always more accurate for larger samples. Thus although for the four tosses there is a good chance (62%) that the H/T ratio will fall outside the range of 0.45 - 0.55, this probability becomes almost zero for 1000 tosses. To express this in a different way, the chances that 1000 gas molecules moving about randomly in a container would at any instant be distributed in a sufficiently non-uniform manner to produce a detectable pressure difference between the two halves of a container will be extremely small. If we increase the number of molecules to a chemically significant number (around 1020, say), then the same probability becomes indistinguishable from zero.
- Once the change begins, it proceeds spontaneously. That is, no external agent (a tosser, shuffler, or teenager) is needed to keep the process going. Gases will spontaneously expand if they are allowed to, and reactions, once started, will proceed toward equilibrium.
- Thermal energy is continually being exchanged between the particles of the system, and between the system and the surroundings. Collisions between molecules result in exchanges of momentum (and thus of kinetic energy) amongst the particles of the system, and (through collisions with the walls of a container, for example) with the surroundings.
- Thermal energy spreads rapidly and randomly throughout the various energetically accessible microstates of the system. The direction of spontaneous change is that which results in the maximum possible spreading and sharing of thermal energy.
The importance of these last two points is far greater than you might at first think, but to fully appreciate this, you must recall the various ways in which thermal energy is stored in molecules.
Sign of Entropy Change
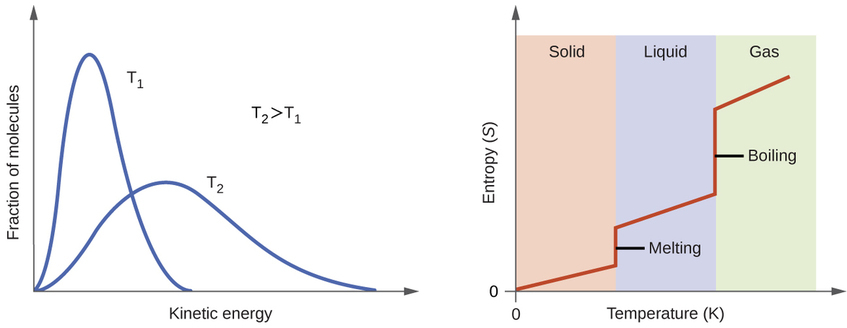
The relationships between entropy, microstates, and matter/energy dispersal described previously allow us to make generalizations regarding the relative entropies of substances and to predict the sign of entropy changes for chemical and physical processes. Consider the phase changes illustrated in Figure \(\PageIndex{4}\). In the solid phase, the atoms or molecules are restricted to nearly fixed positions with respect to each other and are capable of only modest oscillations about these positions. With essentially fixed locations for the system’s component particles, the number of microstates is relatively small. In the liquid phase, the atoms or molecules are free to move over and around each other, though they remain in relatively close proximity to one another. This increased freedom of motion results in a greater variation in possible particle locations, so the number of microstates is correspondingly greater than for the solid. As a result, \(S_{liquid} > S_{solid}\) and the process of converting a substance from solid to liquid (melting) is characterized by an increase in entropy, \(ΔS > 0\). By the same logic, the reciprocal process (freezing) exhibits a decrease in entropy, \(ΔS < 0\).

Now consider the vapor or gas phase. The atoms or molecules occupy a much greater volume than in the liquid phase; therefore each atom or molecule can be found in many more locations than in the liquid (or solid) phase. Consequently, for any substance,
\[S_{gas} \gg S_{liquid} > S_{solid}\]
and the processes of vaporization and sublimation likewise involve increases in entropy, \(ΔS > 0\). Likewise, the reciprocal phase transitions, condensation and deposition, involve decreases in entropy, \(ΔS < 0\).
According to kinetic-molecular theory, the temperature of a substance is proportional to the average kinetic energy of its particles. Raising the temperature of a substance will result in more extensive vibrations of the particles in solids and more rapid translations of the particles in liquids and gases. At higher temperatures, the distribution of kinetic energies among the atoms or molecules of the substance is also broader (more dispersed) than at lower temperatures. Thus, the entropy for any substance increases with temperature (Figure \(\PageIndex{5}\) ).
The entropy of a substance is influenced by structure of the particles (atoms or molecules) that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relation between a particle’s mass and the spacing of quantized translational energy levels (which is a topic beyond the scope of our treatment). For molecules, greater numbers of atoms (regardless of their masses) increase the ways in which the molecules can vibrate and thus the number of possible microstates and the system entropy.
Finally, variations in the types of particles affect the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of two or more different particle types is greater. This is because of the additional orientations and interactions that are possible in a system comprised of nonidentical components. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates. The process of dissolution therefore involves an increase in entropy, \(ΔS > 0\).
Considering the various factors that affect entropy allows us to make informed predictions of the sign of \(ΔS\) for various chemical and physical processes as illustrated in Example \(\PageIndex{2}\).
Predict the sign of the entropy change for the following processes. Indicate the reason for each of your predictions.
- One mole liquid water at room temperature \(⟶\) one mole liquid water at 50 °C
- \(\ce{Ag+}(aq)+\ce{Cl-}(aq)⟶\ce{AgCl}(s)\)
- \(\ce{C6H6(l) + 15/2 O2(g) -> 6CO2(g) + 3H2O(l)}\)
- \(\ce{NH3}(s)⟶\ce{NH3}(l)\)
Solution
- positive, temperature increases
- negative, reduction in the number of ions (particles) in solution, decreased dispersal of matter
- negative, net decrease in the amount of gaseous species
- positive, phase transition from solid to liquid, net increase in dispersal of matter
Predict the sign of the enthalpy change for the following processes. Give a reason for your prediction.
- \(\ce{NaNO3}(s)⟶\ce{Na+}(aq)+\ce{NO3-}(aq)\)
- the freezing of liquid water
- \(\ce{CO2}(s)⟶\ce{CO2}(g)\)
- \(\ce{CaCO}(s)⟶\ce{CaO}(s)+\ce{CO2}(g)\)
- Answer a
-
Positive; The solid dissolves to give an increase of mobile ions in solution.
- Answer b
-
Negative; The liquid becomes a more ordered solid.
- Answer c
-
Positive; The relatively ordered solid becomes a gas.
- Answer d
-
Positive; There is a net production of one mole of gas.
Summary
Entropy (\(S\)) is a state function that can be related to the number of microstates for a system (the number of ways the system can be arranged) and to the ratio of reversible heat to kelvin temperature. It may be interpreted as a measure of the dispersal or distribution of matter and/or energy in a system, and it is often described as representing the “disorder” of the system. For a given substance, \(S_{solid} < S_{liquid} \ll S_{gas}\) in a given physical state at a given temperature, entropy is typically greater for heavier atoms or more complex molecules. Entropy increases when a system is heated and when solutions form. Using these guidelines, the sign of entropy changes for some chemical reactions may be reliably predicted.
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


