10.1: Bulk Properties of Liquids - Molecular Interpretation
- Page ID
- 41586
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To describe the unique properties of liquids.
- To know how and why the vapor pressure of a liquid varies with temperature.
- To understand that the equilibrium vapor pressure of a liquid depends on the temperature and the intermolecular forces present.
Although you have been introduced to some of the interactions that hold molecules together in a liquid, we have not yet discussed the consequences of those interactions for the bulk properties of liquids. We now turn our attention to four unique properties of liquids that intimately depend on the nature of intermolecular interactions:
- surface tension,
- capillary action,
- viscosity, and
- boiling point.
Surface Tension
If liquids tend to adopt the shapes of their containers, then why do small amounts of water on a freshly waxed car form raised droplets instead of forming a thin, continuous film? The answer lies in a property called surface tension, which depends on intermolecular forces. Surface tension is the energy required to increase the surface area of a liquid by a unit amount and varies greatly from liquid to liquid based on the nature of the intermolecular forces, e.g., water with hydrogen bonds has a surface tension of \(7.29 \times 10^{-2} J/m^2\) (at 20°C), while mercury with metallic (electrostatic) bonds has as surface tension that is 6.5-times greater: \(4.86 \times 10^{-1} J/m^2\) (at 20°C).
Figure \(\PageIndex{1}\) presents a microscopic view of a liquid droplet. A typical molecule in the interior of the droplet is surrounded by other molecules that exert attractive forces from all directions. Consequently, there is no net force on the molecule that would cause it to move in a particular direction. In contrast, a molecule on the surface experiences a net attraction toward the drop because there are no molecules on the outside to balance the forces exerted by adjacent molecules in the interior. Because a sphere has the smallest possible surface area for a given volume, intermolecular attractive interactions between water molecules cause the droplet to adopt a spherical shape. This maximizes the number of attractive interactions and minimizes the number of water molecules at the surface. Hence raindrops are almost spherical, and drops of water on a waxed (nonpolar) surface, which does not interact strongly with water, form round beads. A dirty car is covered with a mixture of substances, some of which are polar. Attractive interactions between the polar substances and water cause the water to spread out into a thin film instead of forming beads.
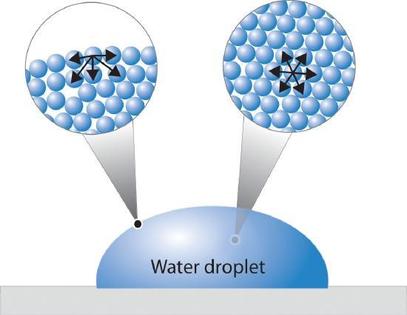
The same phenomenon holds molecules together at the surface of a bulk sample of water, almost as if they formed a skin. When filling a glass with water, the glass can be overfilled so that the level of the liquid actually extends above the rim. Similarly, a sewing needle or a paper clip can be placed on the surface of a glass of water where it “floats,” even though steel is much denser than water. Many insects take advantage of this property to walk on the surface of puddles or ponds without sinking. This is better demonstrated in the zero-gravity conditions of space (Figure \(\PageIndex{2}\)).
Such phenomena are manifestations of surface tension, which is defined as the energy required to increase the surface area of a liquid by a specific amount. Surface tension is therefore measured as energy per unit area, such as joules per square meter (J/m2). The values of the surface tension of some representative liquids are listed in Table \(\PageIndex{2}\). Note the correlation between the surface tension of a liquid and the strength of the intermolecular forces: the stronger the intermolecular forces, the higher the surface tension. For example, water, with its strong intermolecular hydrogen bonding, has one of the highest surface tension values of any liquid, whereas low-boiling-point organic molecules, which have relatively weak intermolecular forces, have much lower surface tensions. Mercury is an apparent anomaly, but its very high surface tension is due to the presence of strong metallic bonding.
| Substance | Surface Tension (× 10−3 J/m2) | Viscosity (mPa•s) | Vapor Pressure (mmHg) | Normal Boiling Point (°C) |
|---|---|---|---|---|
| Organic Compounds | ||||
| diethyl ether | 17 | 0.22 | 531 | 34.6 |
| n-hexane | 18 | 0.30 | 149 | 68.7 |
| acetone | 23 | 0.31 | 227 | 56.5 |
| ethanol | 22 | 1.07 | 59 | 78.3 |
| ethylene glycol | 48 | 16.1 | ~0.08 | 198.9 |
| Liquid Elements | ||||
| bromine | 41 | 0.94 | 218 | 58.8 |
| mercury | 486 | 1.53 | 0.0020 | 357 |
| Water | ||||
| 0°C | 75.6 | 1.79 | 4.6 | — |
| 20°C | 72.8 | 1.00 | 17.5 | — |
| 60°C | 66.2 | 0.47 | 149 | — |
| 100°C | 58.9 | 0.28 | 760 | — |
Adding soaps and detergents that disrupt the intermolecular attractions between adjacent water molecules can reduce the surface tension of water. Because they affect the surface properties of a liquid, soaps and detergents are called surface-active agents, or surfactants. In the 1960s, US Navy researchers developed a method of fighting fires aboard aircraft carriers using “foams,” which are aqueous solutions of fluorinated surfactants. The surfactants reduce the surface tension of water below that of fuel, so the fluorinated solution is able to spread across the burning surface and extinguish the fire. Such foams are now used universally to fight large-scale fires of organic liquids.
Any material - solid, liquid or (non-ideal) gas - wants to bond to itself. This is why condensed phase materials "sticks" together in the first place. However, a surface disrupts this bonding, and so incurs an energy penalty. This is why liquids in zero gravity ball up into spherical drops (Figure \(\PageIndex{2}\)) - the sphere is the shape with the lowest surface area for a fixed volume. We can describe this surface energy with dimensions of energy per unit area, which is the amount of extra energy needed to create new surface or extend a surface (e.g., cracking a solid or parting a liquid). Hence, surface tension is typically given in J/m2 units (Table \(\PageIndex{2}\)).
Capillary Action
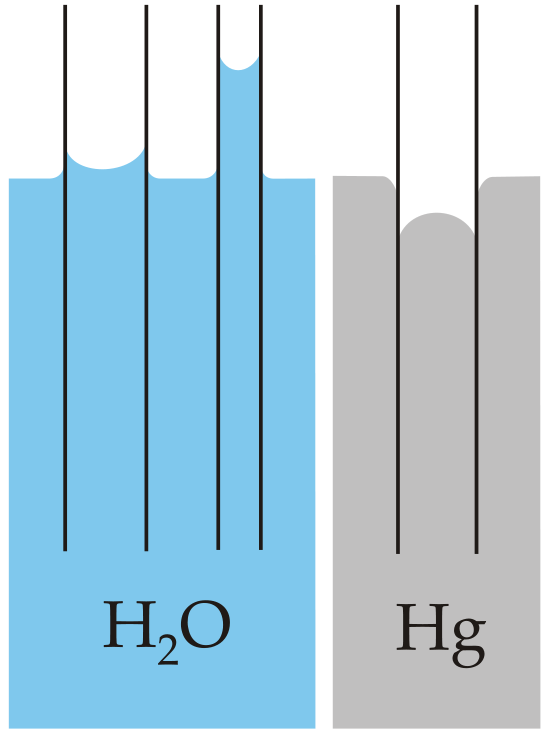
Intermolecular forces also cause a phenomenon called capillary action, which is the tendency of a polar liquid to rise against gravity into a small-diameter tube (a capillary), as shown in Figure \(\PageIndex{3}\). When a glass capillary is put into a dish of water, water is drawn up into the tube. The height to which the water rises depends on the diameter of the tube and the temperature of the water but not on the angle at which the tube enters the water. The smaller the diameter, the higher the liquid rises. The height of the water does not depend on the angle at which the capillary is tilted.

Capillary action is the net result of two opposing sets of forces: cohesive forces, which are the intermolecular forces that hold a liquid together, and adhesive forces, which are the attractive forces between a liquid and the substance that composes the capillary.
- Cohesive forces bind molecules of the same type together
- Adhesive forces bind a substance to a surface
Water has both strong adhesion to glass, which contains polar \(\ce{SiOH}\) groups, and strong intermolecular cohesion. When a glass capillary is put into water, the surface tension due to cohesive forces constricts the surface area of water within the tube, while adhesion between the water and the glass creates an upward force that maximizes the amount of glass surface in contact with the water. If the adhesive forces are stronger than the cohesive forces, as is the case for water, then the liquid in the capillary rises to the level where the downward force of gravity exactly balances this upward force. If, however, the cohesive forces are stronger than the adhesive forces, as is the case for mercury and glass, the liquid pulls itself down into the capillary below the surface of the bulk liquid to minimize contact with the glass (part (a) in Figure \(\PageIndex{4}\)). The upper surface of a liquid in a tube is called the meniscus, and the shape of the meniscus depends on the relative strengths of the cohesive and adhesive forces. In liquids such as water, the meniscus is concave; in liquids such as mercury, however, which have very strong cohesive forces and weak adhesion to glass, the meniscus is convex (Figure \(\PageIndex{4b}\)).
Fluids and nutrients are transported up the stems of plants or the trunks of trees by capillary action. Plants contain tiny rigid tubes composed of cellulose, to which water has strong adhesion. Because of the strong adhesive forces, nutrients can be transported from the roots to the tops of trees that are more than 50 m tall. Cotton towels are also made of cellulose; they absorb water because the tiny tubes act like capillaries and “wick” the water away from your skin. The moisture is absorbed by the entire fabric, not just the layer in contact with your body.
Polar substances are drawn up a glass capillary and generally have concave meniscuses and nonpolar substances general avoid the capillary and exhibit convex meniscuses.
Viscosity
Viscosity (η) is the resistance of a liquid to flow. Some liquids, such as gasoline, ethanol, and water, flow very readily and hence have a low viscosity. Others, such as motor oil, molasses, and maple syrup, flow very slowly and have a high viscosity. The two most common methods for evaluating the viscosity of a liquid are
- to measure the time it takes for a quantity of liquid to flow through a narrow vertical tube and
- to measure the time it takes steel balls to fall through a given volume of the liquid.
The higher the viscosity, the slower the liquid flows through the tube and the steel balls fall. Viscosity is expressed in units of the poise (mPa•s); the higher the number, the higher the viscosity. The viscosities of some representative liquids are listed in Table \(\PageIndex{1}\) and show a correlation between viscosity and intermolecular forces. Because a liquid can flow only if the molecules can move past one another with minimal resistance, strong intermolecular attractive forces make it more difficult for molecules to move with respect to one another. The addition of a second hydroxyl group to ethanol, for example, which produces ethylene glycol (HOCH2CH2OH), increases the viscosity 15-fold. This effect is due to the increased number of hydrogen bonds that can form between hydroxyl groups in adjacent molecules, resulting in dramatically stronger intermolecular attractive forces.
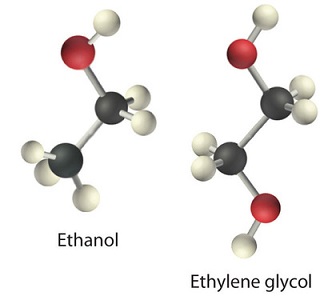
There is also a correlation between viscosity and molecular shape. Liquids consisting of long, flexible molecules tend to have higher viscosities than those composed of more spherical or shorter-chain molecules. The longer the molecules, the easier it is for them to become “tangled” with one another, making it more difficult for them to move past one another. London dispersion forces also increase with chain length. Due to a combination of these two effects, long-chain hydrocarbons (such as motor oils) are highly viscous.
Viscosity increases as intermolecular interactions or molecular size increases.
Motor oils and other lubricants demonstrate the practical importance of controlling viscosity. The oil in an automobile engine must effectively lubricate under a wide range of conditions, from subzero starting temperatures to the 200°C that oil can reach in an engine in the heat of the Mojave Desert in August. Viscosity decreases rapidly with increasing temperatures because the kinetic energy of the molecules increases, and higher kinetic energy enables the molecules to overcome the attractive forces that prevent the liquid from flowing (Table \(\PageIndex{3}\)). As a result, an oil that is thin enough to be a good lubricant in a cold engine will become too “thin” (have too low a viscosity) to be effective at high temperatures.
The viscosity of motor oils is described by an SAE (Society of Automotive Engineers) rating ranging from SAE 5 to SAE 50 for engine oils: the lower the number, the lower the viscosity. So-called single-grade oils can cause major problems. If they are viscous enough to work at high operating temperatures (SAE 50, for example), then at low temperatures, they can be so viscous that a car is difficult to start or an engine is not properly lubricated. Consequently, most modern oils are multigrade, with designations such as SAE 20W/50 (a grade used in high-performance sports cars), in which case the oil has the viscosity of an SAE 20 oil at subzero temperatures (hence the W for winter) and the viscosity of an SAE 50 oil at high temperatures. These properties are achieved by a careful blend of additives that modulate the intermolecular interactions in the oil, thereby controlling the temperature dependence of the viscosity. Many of the commercially available oil additives “for improved engine performance” are highly viscous materials that increase the viscosity and effective SAE rating of the oil, but overusing these additives can cause the same problems experienced with highly viscous single-grade oils.
| SAE | Temperature (oC) | |||
|---|---|---|---|---|
| 0 | 20 | 50 | 100 | |
| 10 | 0.31 | 0.079 | 0.020 | 0.005 |
| 20 | 0.72 | 0.170 | 0.033 | 0.007 |
| 30 | 1.53 | 0.310 | 0.061 | 0.010 |
| 40 | 2.61 | 0.430 | 0.072 | 0.012 |
| 50 | 3.82 | 0.630 | 0.097 | 0.015 |
Based on the nature and strength of the intermolecular cohesive forces and the probable nature of the liquid–glass adhesive forces, predict what will happen when a glass capillary is put into a beaker of SAE 20 motor oil. Will the oil be pulled up into the tube by capillary action or pushed down below the surface of the liquid in the beaker? What will be the shape of the meniscus (convex or concave)? (Hint: the surface of glass is lined with Si–OH groups.)
Given: substance and composition of the glass surface
Asked for: behavior of oil and the shape of meniscus
Strategy:
- Identify the cohesive forces in the motor oil.
- Determine whether the forces interact with the surface of glass. From the strength of this interaction, predict the behavior of the oil and the shape of the meniscus.
Solution:
A Motor oil is a nonpolar liquid consisting largely of hydrocarbon chains. The cohesive forces responsible for its high boiling point are almost solely London dispersion forces between the hydrocarbon chains.
B Such a liquid cannot form strong interactions with the polar Si–OH groups of glass, so the surface of the oil inside the capillary will be lower than the level of the liquid in the beaker. The oil will have a convex meniscus similar to that of mercury.
Predict what will happen when a glass capillary is put into a beaker of ethylene glycol. Will the ethylene glycol be pulled up into the tube by capillary action or pushed down below the surface of the liquid in the beaker? What will be the shape of the meniscus (convex or concave)?
- Answer
-
Capillary action will pull the ethylene glycol up into the capillary. The meniscus will be concave.
Superfluid helium-4 is the superfluid form of helium-4, an isotope of the element helium. A superfluid is a state of matter in which the matter behaves like a fluid with zero viscosity. The substance, which looks like a normal liquid, flows without friction past any surface, which allows it to continue to circulate over obstructions and through pores in containers which hold it, subject only to its own inertia.

Many ordinary fluids, like alcohol or petroleum, creep up solid walls, driven by their surface tension. However, in the case of superfluid helium-4, the flow of the liquid in the layer is not restricted by its viscosity but by a critical velocity which is about 20 cm/s. This is a fairly high velocity so superfluid helium can flow relatively easily up the wall of containers, over the top, and down to the same level as the surface of the liquid inside the container. In a container, lifted above the liquid level, it forms visible droplets as seen above.
Boiling Points
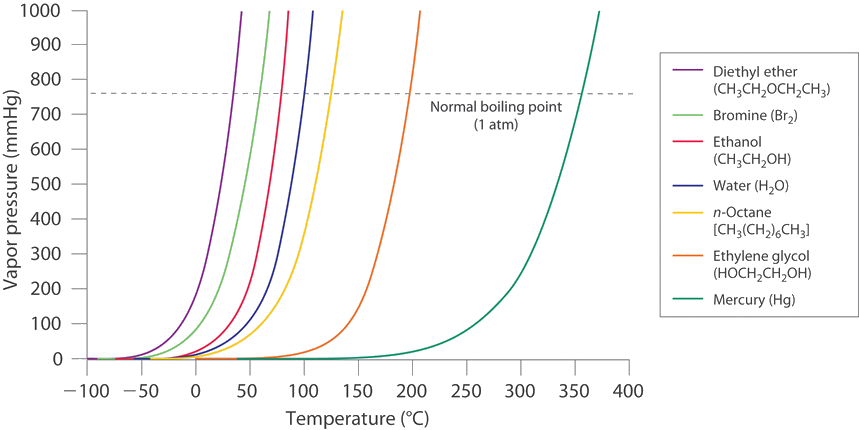
The vapor pressure of a liquid is defined as the pressure exerted by a vapor in equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system (discussed in more detail in next Sections of Chapter). As the temperature of a liquid increases, the vapor pressure of the liquid increases until it equals the external pressure, or the atmospheric pressure in the case of an open container. Bubbles of vapor begin to form throughout the liquid, and the liquid begins to boil. The temperature at which a liquid boils at exactly 1 atm pressure is the normal boiling point of the liquid. For water, the normal boiling point is exactly 100°C. The normal boiling points of the other liquids in Figure \(\PageIndex{8}\) are represented by the points at which the vapor pressure curves cross the line corresponding to a pressure of 1 atm.
Although we usually cite the normal boiling point of a liquid, the actual boiling point depends on the pressure. At a pressure greater than 1 atm, water boils at a temperature greater than 100°C because the increased pressure forces vapor molecules above the surface to condense. Hence the molecules must have greater kinetic energy to escape from the surface. Conversely, at pressures less than 1 atm, water boils below 100°C.
| Place | Altitude above Sea Level (ft) | Atmospheric Pressure (mmHg) | Boiling Point of Water (°C) |
|---|---|---|---|
| Mt. Everest, Nepal/Tibet | 29,028 | 240 | 70 |
| Bogota, Colombia | 11,490 | 495 | 88 |
| Denver, Colorado | 5280 | 633 | 95 |
| Washington, DC | 25 | 759 | 100 |
| Dead Sea, Israel/Jordan | −1312 | 799 | 101.4 |
Typical variations in atmospheric pressure at sea level are relatively small, causing only minor changes in the boiling point of water. For example, the highest recorded atmospheric pressure at sea level is 813 mmHg, recorded during a Siberian winter; the lowest sea-level pressure ever measured was 658 mmHg in a Pacific typhoon. At these pressures, the boiling point of water changes minimally, to 102°C and 96°C, respectively. At high altitudes, on the other hand, the dependence of the boiling point of water on pressure becomes significant. Table \(\PageIndex{4}\) lists the boiling points of water at several locations with different altitudes. At an elevation of only 5000 ft, for example, the boiling point of water is already lower than the lowest ever recorded at sea level. The lower boiling point of water has major consequences for cooking everything from soft-boiled eggs (a “three-minute egg” may well take four or more minutes in the Rockies and even longer in the Himalayas) to cakes (cake mixes are often sold with separate high-altitude instructions). Conversely, pressure cookers, which have a seal that allows the pressure inside them to exceed 1 atm, are used to cook food more rapidly by raising the boiling point of water and thus the temperature at which the food is being cooked.
As pressure increases, the boiling point of a liquid increases and vice versa.
Use Figure \(\PageIndex{8}\) to estimate the following.
- the boiling point of water in a pressure cooker operating at 1000 mmHg
- the pressure required for mercury to boil at 250°C
Mercury boils at 356 °C at room pressure. To see video go to www.youtube.com/watch?v=0iizsbXWYoo
Given: data in Figure \(\PageIndex{8}\), pressure, and boiling point
Asked for: corresponding boiling point and pressure
Strategy:
- To estimate the boiling point of water at 1000 mmHg, refer to Figure \(\PageIndex{8}\) and find the point where the vapor pressure curve of water intersects the line corresponding to a pressure of 1000 mmHg.
- To estimate the pressure required for mercury to boil at 250°C, find the point where the vapor pressure curve of mercury intersects the line corresponding to a temperature of 250°C.
Solution:
- The vapor pressure curve of water intersects the P = 1000 mmHg line at about 110°C; this is therefore the boiling point of water at 1000 mmHg.
- The vertical line corresponding to 250°C intersects the vapor pressure curve of mercury at P ≈ 75 mmHg. Hence this is the pressure required for mercury to boil at 250°C.
Ethylene glycol is an organic compound primarily used as a raw material in the manufacture of polyester fibers and fabric industry, and polyethylene terephthalate resins (PET) used in bottling. Use the data in Figure \(\PageIndex{8}\) to estimate the following.
- the normal boiling point of ethylene glycol
- the pressure required for diethyl ether to boil at 20°C.
- Answer a
-
200°C
- Answer b
-
450 mmHg
Summary
Surface tension, capillary action, boiling points, and viscosity are unique properties of liquids that depend on the nature of intermolecular interactions. Surface tension is the energy required to increase the surface area of a liquid by a given amount. The stronger the intermolecular interactions, the greater the surface tension. Surfactants are molecules, such as soaps and detergents, that reduce the surface tension of polar liquids like water. Capillary action is the phenomenon in which liquids rise up into a narrow tube called a capillary. It results when cohesive forces, the intermolecular forces in the liquid, are weaker than adhesive forces, the attraction between a liquid and the surface of the capillary. The shape of the meniscus, the upper surface of a liquid in a tube, also reflects the balance between adhesive and cohesive forces. The viscosity of a liquid is its resistance to flow. Liquids that have strong intermolecular forces tend to have high viscosities. The boiling point of a liquid is the temperature when the vapor pressure of the liquid equals the external pressure, or the atmospheric pressure in the case of an open container.
Contributors and Attributions
Modified by Joshua Halpern (Howard University)

