13.6: Vapor Pressures of Solutions
- Page ID
- 24258
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To describe the relationship between solute concentration and the physical properties of a solution.
- To understand that the total number of nonvolatile solute particles determines the decrease in vapor pressure, increase in boiling point, and decrease in freezing point of a solution versus the pure solvent.
Raoult’s Law
Adding a nonvolatile solute, one whose vapor pressure is too low to measure readily, to a volatile solvent decreases the vapor pressure of the solvent. We can understand this phenomenon qualitatively by examining Figure \(\PageIndex{1}\), which is a schematic diagram of the surface of a solution of glucose in water. In an aqueous solution of glucose, a portion of the surface area is occupied by nonvolatile glucose molecules rather than by volatile water molecules. As a result, fewer water molecules can enter the vapor phase per unit time, even though the surface water molecules have the same kinetic energy distribution as they would in pure water. At the same time, the rate at which water molecules in the vapor phase collide with the surface and reenter the solution is unaffected. The net effect is to shift the dynamic equilibrium between water in the vapor and the liquid phases, decreasing the vapor pressure of the solution compared with the vapor pressure of the pure solvent.
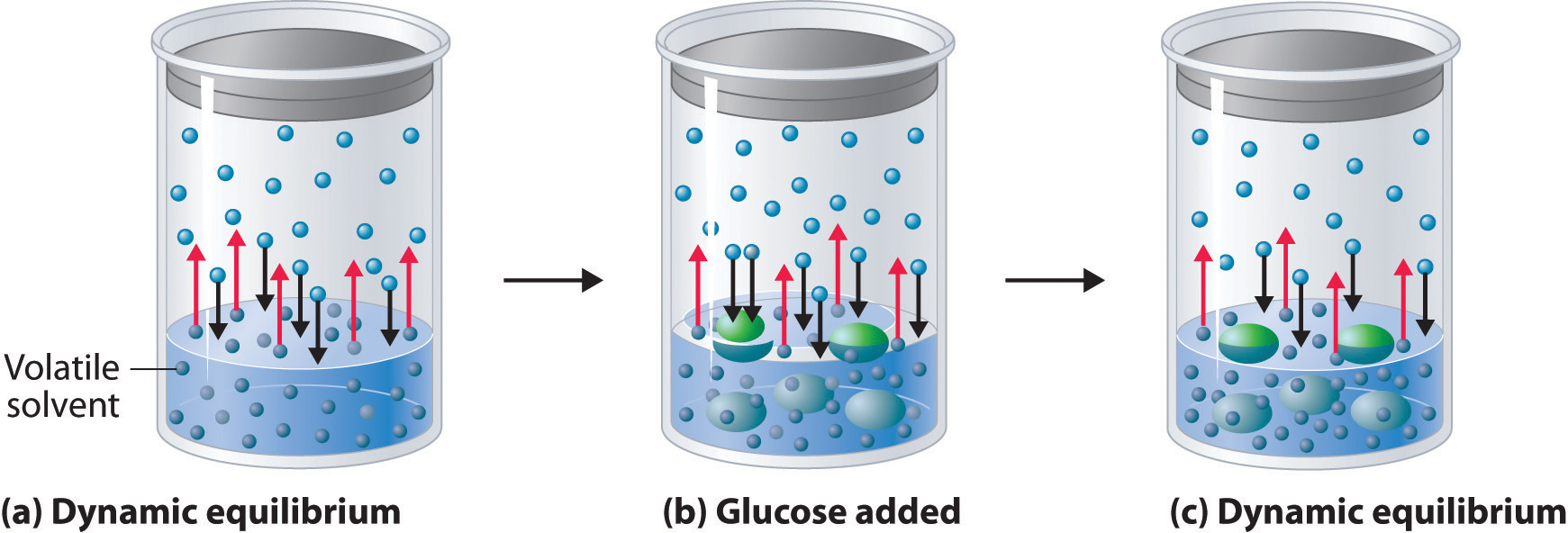
Figure \(\PageIndex{2}\) shows two beakers, one containing pure water and one containing an aqueous glucose solution, in a sealed chamber. We can view the system as having two competing equilibria: water vapor will condense in both beakers at the same rate, but water molecules will evaporate more slowly from the glucose solution because fewer water molecules are at the surface. Eventually all of the water will evaporate from the beaker containing the liquid with the higher vapor pressure (pure water) and condense in the beaker containing the liquid with the lower vapor pressure (the glucose solution). If the system consisted of only a beaker of water inside a sealed container, equilibrium between the liquid and vapor would be achieved rather rapidly, and the amount of liquid water in the beaker would remain constant.
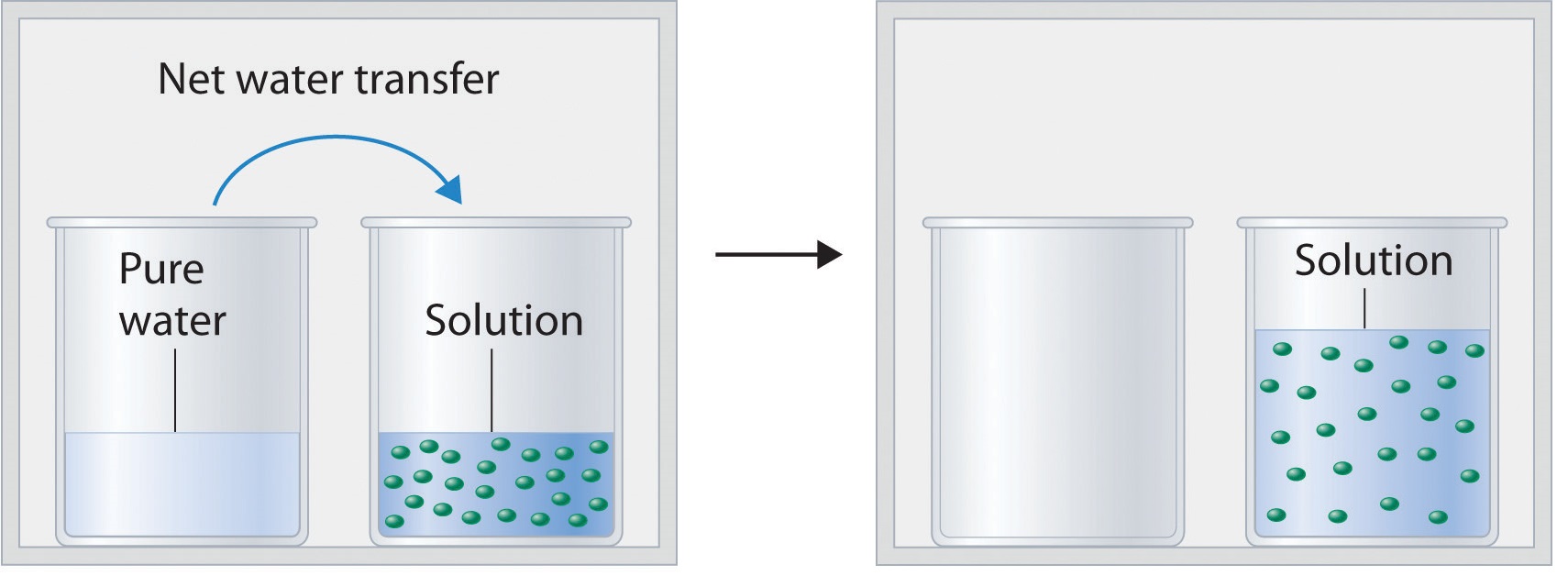
If the particles of a solute are essentially the same size as those of the solvent and both solute and solvent have roughly equal probabilities of being at the surface of the solution, then the effect of a solute on the vapor pressure of the solvent is proportional to the number of sites occupied by solute particles at the surface of the solution. Doubling the concentration of a given solute causes twice as many surface sites to be occupied by solute molecules, resulting in twice the decrease in vapor pressure. The relationship between solution composition and vapor pressure is therefore
\[ \color{red} P_A=X_AP^0_A \label{13.6.1}\]
where \(P_A\) is the vapor pressure of component A of the solution (in this case the solvent), XA is the mole fraction of A in solution, and \(P^0_A\) is the vapor pressure of pure A. Equation \ref{13.6.1} is known as Raoult’s law, after the French chemist who developed it. If the solution contains only a single nonvolatile solute (B), then \(X_A + X_B = 1\), and we can substitute \(X_A = 1 − X_B\) to obtain
\[\begin{align} P_A &=(1−X_B)P^0_A \\[4pt] &=P^0_A−X_BP^0_A \label{13.6.2} \end{align}\]
Rearranging and defining \(ΔP_A=P^0_A−P_A\), we obtain a relationship between the decrease in vapor pressure and the mole fraction of nonvolatile solute:
\[P^0_A−P_A=ΔP_A=X_BP^0_A \label{13.6.3}\]
We can solve vapor pressure problems in either of two ways: by using Equation \ref{13.6.1} to calculate the actual vapor pressure above a solution of a nonvolatile solute, or by using Equation \ref{13.6.3} to calculate the decrease in vapor pressure caused by a specified amount of a nonvolatile solute.
Ethylene glycol (\(\ce{HOCH_2CH_2OH}\)), the major ingredient in commercial automotive antifreeze, increases the boiling point of radiator fluid by lowering its vapor pressure. At 100°C, the vapor pressure of pure water is 760 mmHg. Calculate the vapor pressure of an aqueous solution containing 30.2% ethylene glycol by mass, a concentration commonly used in climates that do not get extremely cold in winter.
Given: identity of solute, percentage by mass, and vapor pressure of pure solvent
Asked for: vapor pressure of solution
Strategy:
- Calculate the number of moles of ethylene glycol in an arbitrary quantity of water, and then calculate the mole fraction of water.
- Use Raoult’s law to calculate the vapor pressure of the solution.
Solution:
A A 30.2% solution of ethylene glycol contains 302 g of ethylene glycol per kilogram of solution; the remainder (698 g) is water. To use Raoult’s law to calculate the vapor pressure of the solution, we must know the mole fraction of water. Thus we must first calculate the number of moles of both ethylene glycol (EG) and water present:
\[moles \; EG=(302 \;\cancel{g}) \left( \dfrac{1\; mol}{62.07\; \cancel{g}} \right)=4.87\; mol\; EG \nonumber\]
\[moles \; \ce{H2O}=(698 \;\cancel{g}) \left( \dfrac{1\; mol}{18.02\; \cancel{g}} \right)=38.7\; mol\; H_2O \nonumber\]
The mole fraction of water is thus
\[X_{\ce{H2O}}=\dfrac{38.7\; \cancel{mol} \; H_2O}{38.7\; \cancel{mol}\; H_2O +4.87 \cancel{mol}\; EG} =0.888 \nonumber\]
B From Raoult’s law (Equation \ref{13.6.1}), the vapor pressure of the solution is
\[P_{\ce{H2O}}=(X_{H2_O})(P^0_{H2_O)}=(0.888)(760\; mmHg) =675 \;mmHg \nonumber\]
Alternatively, we could solve this problem by calculating the mole fraction of ethylene glycol and then using Equation \ref{13.6.3} to calculate the resulting decrease in vapor pressure:
\[X_{EG}=\dfrac{4.87\; mol\; EG}{4.87\; mol\; EG+38.7\; mol\; H_2O}=0.112 \nonumber\]
\[ΔP_{\ce{H2O}}=(X_{EG})(P^0_{H_2O})=(0.112)(760\; mmHg)=85.1\; mmHg \nonumber\]
\[P_{\ce{H2O}}=P^0H_2O−ΔP_{H_2O}=760\; mmHg−85.1\; mmHg=675\; mmHg \nonumber\]
The same result is obtained using either method.
Seawater is an approximately 3.0% aqueous solution of \(NaCl\) by mass with about 0.5% of other salts by mass. Calculate the decrease in the vapor pressure of water at 25°C caused by this concentration of \(NaCl\), remembering that 1 mol of \(NaCl\) produces 2 mol of solute particles. The vapor pressure of pure water at 25°C is 23.8 mmHg.
- Answer
-
0.45 mmHg. This may seem like a small amount, but it constitutes about a 2% decrease in the vapor pressure of water and accounts in part for the higher humidity in the north-central United States near the Great Lakes, which are freshwater lakes. The decrease therefore has important implications for climate modeling.
Finding the Vapor Pressure of a Solution (Ionic-Nonvolatile Solute):
Volatile Solutes
Even when a solute is volatile, meaning that it has a measurable vapor pressure, we can still use Raoult’s law. In this case, we calculate the vapor pressure of each component separately. The total vapor pressure of the solution (\(P_T\)) is the sum of the vapor pressures of the components:
\[ \begin{align} P_T &=P_A+P_B \\[4pt] &=X_AP^0_A+X_BP^0_B \label{13.6.4} \end{align}\]
Because \(X_B = 1 − X_A\) for a two-component system,
\[ P_T=X_AP^0_A+(1−X_A)P^0_B \label{13.6.5}\]
Thus we need to specify the mole fraction of only one of the components in a two-component system. Consider, for example, the vapor pressure of solutions of benzene and toluene of various compositions. At 20°C, the vapor pressures of pure benzene and toluene are 74.7 and 22.3 mmHg, respectively. The vapor pressure of benzene in a benzene–toluene solution is
\[P_{C_6H_6}=X_{C_6H_6}P^0_{C_6H_6} \label{13.6.6}\]
and the vapor pressure of toluene in the solution is
\[P_{C_6H_5CH_3}=X_{C_6H_5CH_3}P^0_{C_6H_5CH3} \label{13.6.7}\]
Equations \ref{13.6.6} and \ref{13.6.7} are both in the form of the equation for a straight line: \(y = mx + b\), where \(b = 0\). Plots of the vapor pressures of both components versus the mole fractions are therefore straight lines that pass through the origin, as shown in Figure Figure \(\PageIndex{3}\). Furthermore, a plot of the total vapor pressure of the solution versus the mole fraction is a straight line that represents the sum of the vapor pressures of the pure components. Thus the vapor pressure of the solution is always greater than the vapor pressure of either component.
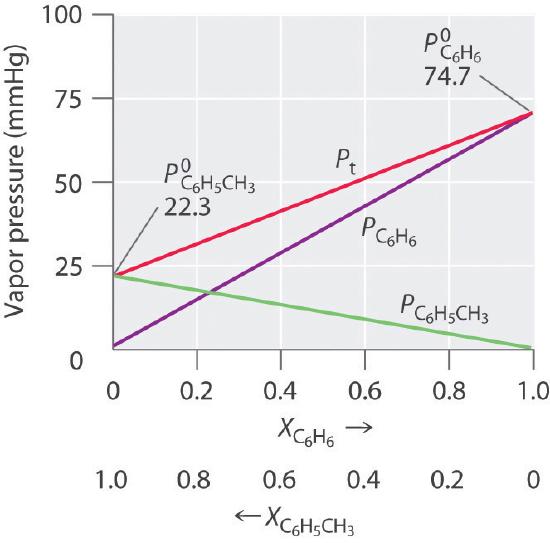
A solution of two volatile components that behaves like the solution in Figure \(\PageIndex{3}\), which is defined as a solution that obeys Raoult’s law. Like an ideal gas, an ideal solution is a hypothetical system whose properties can be described in terms of a simple model. Mixtures of benzene and toluene approximate an ideal solution because the intermolecular forces in the two pure liquids are almost identical in both kind and magnitude. Consequently, the change in enthalpy on solution formation is essentially zero (\(ΔH_{soln} ≈ 0\)), which is one of the defining characteristics of an ideal solution.
Ideal solutions and ideal gases are both simple models that ignore intermolecular interactions.
Most real solutions, however, do not obey Raoult’s law precisely, just as most real gases do not obey the ideal gas law exactly. Real solutions generally deviate from Raoult’s law because the intermolecular interactions between the two components A and B differ. We can distinguish between two general kinds of behavior, depending on whether the intermolecular interactions between molecules A and B are stronger or weaker than the A–A and B–B interactions in the pure components. If the A–B interactions are stronger than the A–A and B–B interactions, each component of the solution exhibits a lower vapor pressure than expected for an ideal solution, as does the solution as a whole. The favorable A–B interactions effectively stabilize the solution compared with the vapor. This kind of behavior is called a negative deviation from Raoult’s law. Systems stabilized by hydrogen bonding between two molecules, such as acetone and ethanol, exhibit negative deviations from Raoult’s law. Conversely, if the A–B interactions are weaker than the A–A and B–B interactions yet the entropy increase is enough to allow the solution to form, both A and B have an increased tendency to escape from the solution into the vapor phase. The result is a higher vapor pressure than expected for an ideal solution, producing a positive deviation from Raoult’s law. In a solution of \(CCl_4\) and methanol, for example, the nonpolar \(CCl_4\) molecules interrupt the extensive hydrogen bonding network in methanol, and the lighter methanol molecules have weaker London dispersion forces than the heavier \(CCl_4\) molecules. Consequently, solutions of \(CCl_4\) and methanol exhibit positive deviations from Raoult’s law.
For each system, compare the intermolecular interactions in the pure liquids and in the solution to decide whether the vapor pressure will be greater than that predicted by Raoult’s law (positive deviation), approximately equal to that predicted by Raoult’s law (an ideal solution), or less than the pressure predicted by Raoult’s law (negative deviation).
- cyclohexane and ethanol
- methanol and acetone
- n-hexane and isooctane (2,2,4-trimethylpentane)
Given: identity of pure liquids
Asked for: predicted deviation from Raoult’s law
Strategy:
Identify whether each liquid is polar or nonpolar, and then predict the type of intermolecular interactions that occur in solution.
Solution:
- Liquid ethanol contains an extensive hydrogen bonding network, and cyclohexane is nonpolar. Because the cyclohexane molecules cannot interact favorably with the polar ethanol molecules, they will disrupt the hydrogen bonding. Hence the A–B interactions will be weaker than the A–A and B–B interactions, leading to a higher vapor pressure than predicted by Raoult’s law (a positive deviation).
- Methanol contains an extensive hydrogen bonding network, but in this case the polar acetone molecules create A–B interactions that are stronger than the A–A or B–B interactions, leading to a negative enthalpy of solution and a lower vapor pressure than predicted by Raoult’s law (a negative deviation).
- Hexane and isooctane are both nonpolar molecules (isooctane actually has a very small dipole moment, but it is so small that it can be ignored). Hence the predominant intermolecular forces in both liquids are London dispersion forces. We expect the A–B interactions to be comparable in strength to the A–A and B–B interactions, leading to a vapor pressure in good agreement with that predicted by Raoult’s law (an ideal solution).
For each system, compare the intermolecular interactions in the pure liquids with those in the solution to decide whether the vapor pressure will be greater than that predicted by Raoult’s law (positive deviation), approximately equal to that predicted by Raoult’s law (an ideal solution), or less than the pressure predicted by Raoult’s law (negative deviation):
- benzene and n-hexane
- ethylene glycol and \(\ce{CCl_4}\)
- acetic acid and n-propanol
- Answer a
-
approximately equal
- Answer b
-
positive deviation (vapor pressure greater than predicted)
- Answer c
-
negative deviation (vapor pressure less than predicted)
Finding Vapor Pressure of a Solution (Nonionic-Volatile Solute):
Summary
- Henry’s law: \[C = kP \nonumber\]
- Raoult’s law: \[P_A=X_AP^0_A \nonumber\]
- vapor pressure lowering: \[P^0_A−P_A=ΔP_A=X_BP^0_A \nonumber\]
- vapor pressure of a system containing two volatile components: \[P_T=X_AP^0_A+(1−X_A)P^0_B \nonumber\]
The vapor pressure of the solution is proportional to the mole fraction of solvent in the solution, a relationship known as Raoult’s law. Solutions that obey Raoult’s law are called ideal solutions. Most real solutions exhibit positive or negative deviations from Raoult’s law.
Contributors and Attributions
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

