11.4: Multiple Covalent Bonds
- Page ID
- 36871
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To explain resonance structures using molecular orbitals.
So far in our molecular orbital descriptions we have not dealt with polyatomic systems with multiple bonds. To do so, we can use an approach in which we describe \(\sigma\) bonding using localized electron-pair bonds formed by hybrid atomic orbitals, and \(\pi\) bonding using molecular orbitals formed by unhybridized np atomic orbitals.
Non-singular Bonding
We begin our discussion by considering the bonding in ethylene (C2H4). Experimentally, we know that the H–C–H and H–C–C angles in ethylene are approximately 120°. This angle suggests that the carbon atoms are sp2 hybridized, which means that a singly occupied sp2 orbital on one carbon overlaps with a singly occupied s orbital on each H and a singly occupied sp2 lobe on the other C. Thus each carbon forms a set of three \(\sigma\) bonds: two C–H (sp2 + s) and one C–C (sp2 + sp2) (part (a) in Figure \(\PageIndex{1}\)). The sp2 hybridization can be represented as follows:

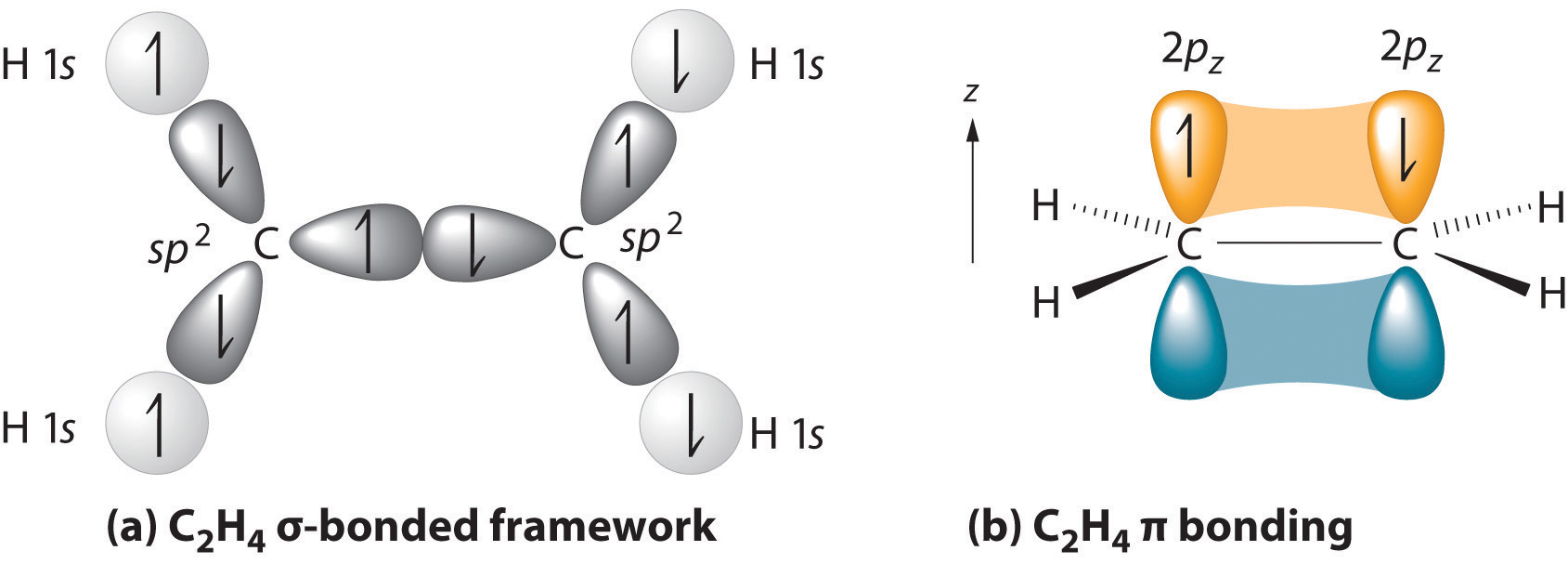
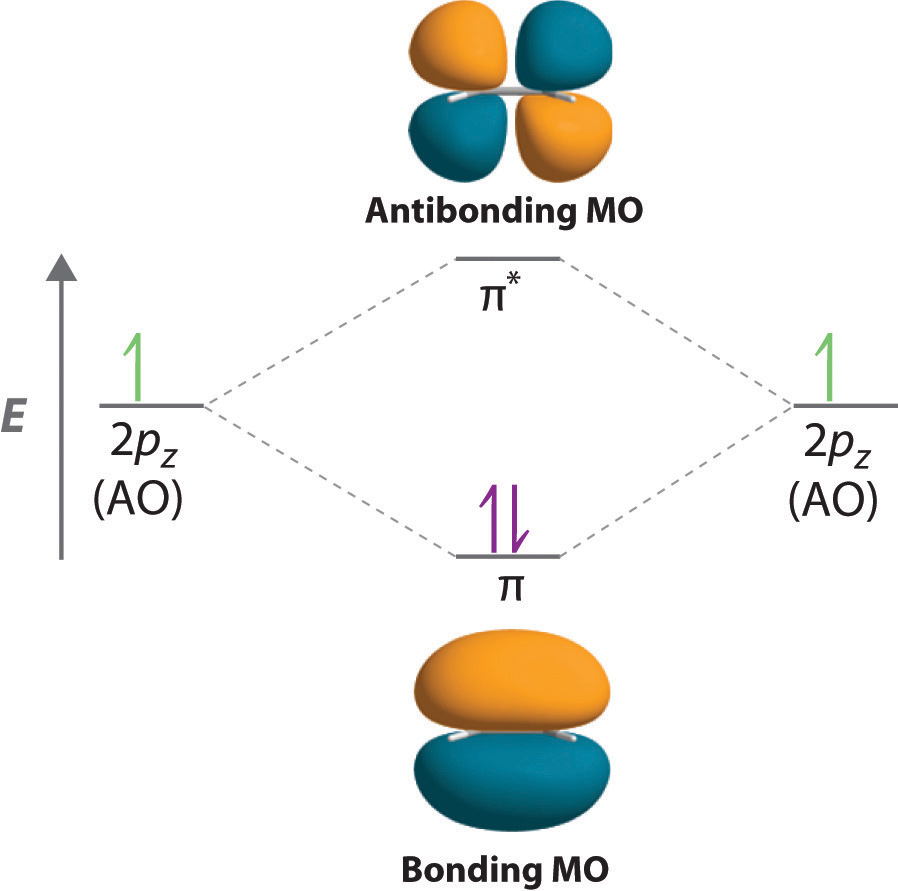
After hybridization, each carbon still has one unhybridized 2pz orbital that is perpendicular to the hybridized lobes and contains a single electron (part (b) in Figure \(\PageIndex{1}\)). The two singly occupied 2pz orbitals can overlap to form a \(\pi\) bonding orbital and a \(\pi\)* antibonding orbital, which produces the energy-level diagram shown in Figure \(\PageIndex{2}\). With the formation of a \(\pi\) bonding orbital, electron density increases in the plane between the carbon nuclei. The \(\pi\)* orbital lies outside the internuclear region and has a nodal plane perpendicular to the internuclear axis. Because each 2pz orbital has a single electron, there are only two electrons, enough to fill only the bonding (\(\pi\)) level, leaving the \(\pi\)* orbital empty. Consequently, the C–C bond in ethylene consists of a \(\sigma\) bond and a \(\pi\) bond, which together give a C=C double bond. Our model is supported by the facts that the measured carbon–carbon bond is shorter than that in ethane (133.9 pm versus 153.5 pm) and the bond is stronger (728 kJ/mol versus 376 kJ/mol in ethane). The two CH2 fragments are coplanar, which maximizes the overlap of the two singly occupied 2pz orbitals.
sp2 Hybridization: https://youtu.be/EepTvePnfBA
Triple bonds, as in acetylene (C2H2), can also be explained using a combination of hybrid atomic orbitals and molecular orbitals. The four atoms of acetylene are collinear, which suggests that each carbon is sp hybridized. If one sp lobe on each carbon atom is used to form a C–C \(\sigma\) bond and one is used to form the C–H \(\sigma\) bond, then each carbon will still have two unhybridized 2p orbitals (a 2px,y pair), each with one electron (part (a) in Figure \(\PageIndex{3}\)).
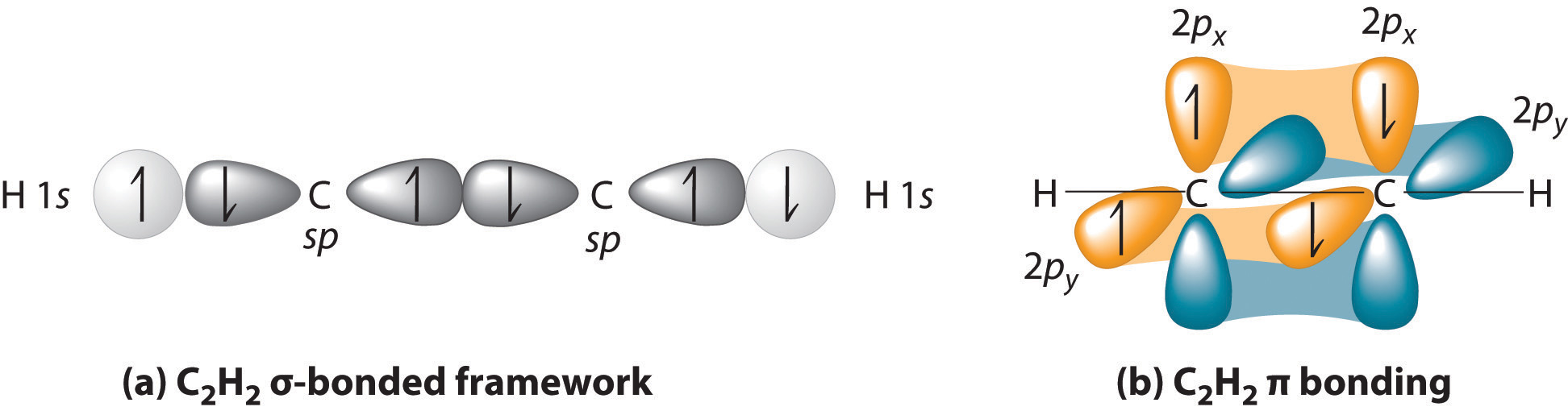
Figure \(\PageIndex{3}\): Bonding in Acetylene (a) In the formation of the \(\sigma\)-bonded framework, two sets of singly occupied carbon sp hybrid orbitals and two singly occupied hydrogen 1s orbitals overlap. (b) In the formation of two carbon–carbon \(\pi\) bonds in acetylene, two singly occupied unhybridized 2px,y orbitals on each carbon atom overlap. With one \(\sigma\) bond plus two \(\pi\) bonds, the carbon–carbon bond order in acetylene is 3.
In complex molecules, hybrid orbitals and valence bond theory can be used to describe \(\sigma\) bonding, and unhybridized \(\pi\) orbitals and molecular orbital theory can be used to describe \(\pi\) bonding.
Describe the bonding in HCN using a combination of hybrid atomic orbitals and molecular orbitals. The HCN molecule is linear.
Given: chemical compound and molecular geometry
Asked for: bonding description using hybrid atomic orbitals and molecular orbitals
Strategy:
- From the geometry given, predict the hybridization in HCN. Use the hybrid orbitals to form the \(\sigma\)-bonded framework of the molecule and determine the number of valence electrons that are used for \(\sigma\) bonding.
- Determine the number of remaining valence electrons. Use any remaining unhybridized p orbitals to form \(\pi\) and \(\pi\)* orbitals.
- Fill the orbitals with the remaining electrons in order of increasing energy. Describe the bonding in HCN.
Solution:
A Because HCN is a linear molecule, it is likely that the bonding can be described in terms of sp hybridization at carbon. Because the nitrogen atom can also be described as sp hybridized, we can use one sp hybrid on each atom to form a C–N \(\sigma\) bond. This leaves one sp hybrid on each atom to either bond to hydrogen (C) or hold a lone pair of electrons (N). Of 10 valence electrons (5 from N, 4 from C, and 1 from H), 4 are used for \(\sigma\) bonding:
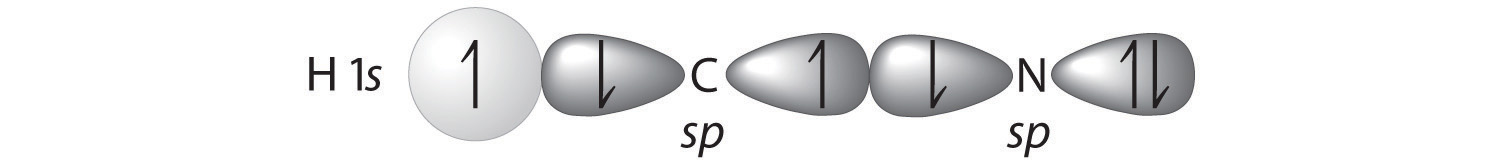
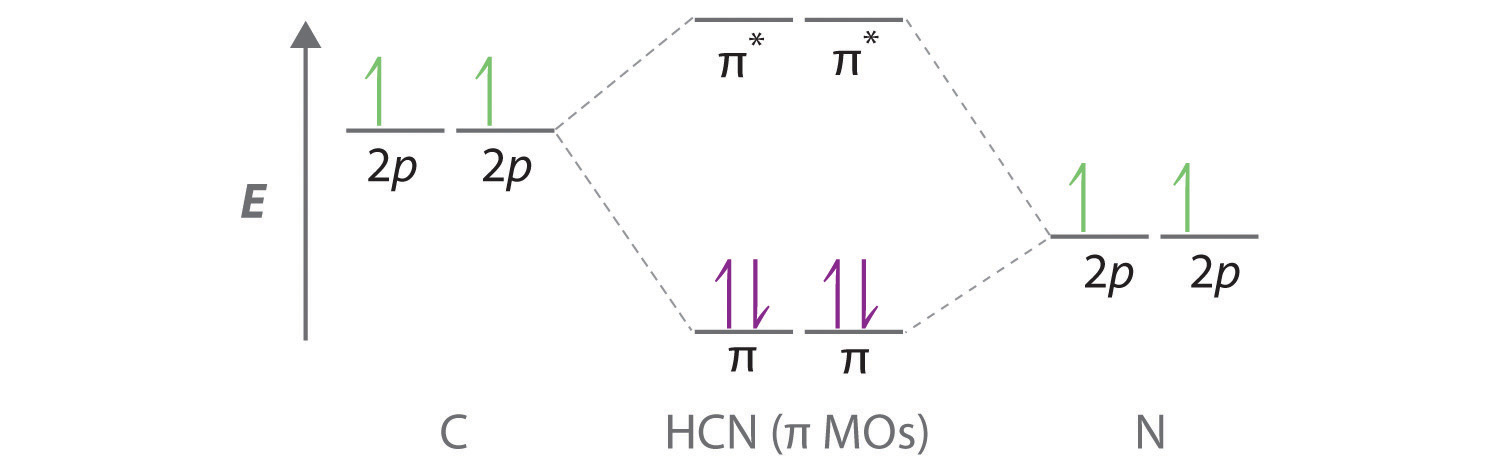
B We are now left with 2 electrons on N (5 valence electrons minus 1 bonding electron minus 2 electrons in the lone pair) and 2 electrons on C (4 valence electrons minus 2 bonding electrons). We have two unhybridized 2p atomic orbitals left on carbon and two on nitrogen, each occupied by a single electron. These four 2p atomic orbitals can be combined to give four molecular orbitals: two \(\pi\) (bonding) orbitals and two \(\pi\)* (antibonding) orbitals. C With 4 electrons available, only the \(\pi\) orbitals are filled. The overall result is a triple bond (1 \(\sigma\) and 2 \(\pi\)) between C and N.
Describe the bonding in formaldehyde (H2C=O), a trigonal planar molecule, using a combination of hybrid atomic orbitals and molecular orbitals.
Answer
- \(\sigma\)-bonding framework: Carbon and oxygen are sp2 hybridized. Two sp2 hybrid orbitals on oxygen have lone pairs, two sp2 hybrid orbitals on carbon form C–H bonds, and one sp2 hybrid orbital on C and O forms a C–O \(\sigma\) bond.
- \(\pi\) bonding: Unhybridized, singly occupied 2p atomic orbitals on carbon and oxygen interact to form \(\pi\) (bonding) and \(\pi\)* (antibonding) molecular orbitals. With two electrons, only the \(\pi\) (bonding) orbital is occupied.
sp Hybridization: https://youtu.be/epQXzG9WDRw
Summary
- Polyatomic systems with multiple bonds can be described using hybrid atomic orbitals for \(\sigma\) bonding and molecular orbitals to describe \(\pi\) bonding.
To describe the bonding in more complex molecules with multiple bonds, we can use an approach that uses hybrid atomic orbitals to describe the \(\sigma\) bonding and molecular orbitals to describe the \(\pi\) bonding. In this approach, unhybridized np orbitals on atoms bonded to one another are allowed to interact to produce bonding, antibonding, or nonbonding combinations. For \(\pi\) bonds between two atoms (as in ethylene or acetylene), the resulting molecular orbitals are virtually identical to the \(\pi\) molecular orbitals in diatomic molecules such as O2 and N2.

