1.5: Density and Percent Composition - Their Use in Problem Solving
- Page ID
- 13779
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To be introduced to the concepts of Density and Percent Composition as important properties of matter.
Density and percent composition are important properties in chemistry. Each have basic components as well as broad applications. Components of density are: mass and volume, both of which can be more confusing than at first glance. An application of the concept of density is determining the volume of an irregular shape using a known mass and density. Determining Percent Composition requires knowing the mass of entire object or molecule and the mass of its components.
Introduction
Which one weighs more, a kilogram of feathers or a kilogram of bricks? Though many people will say that a kilogram of bricks is heavier, they actually weigh the same! However, many people are caught up by the concept of density \(\rho\), which causes them to answer the question incorrectly. A kilogram of feathers clearly takes up more space, but this is because it is less "dense." But what is density, and how can we determine it?
In the laboratory, density can be used to identify an element, while percent composition is used to determine the amount, by mass, of each element present in a chemical compound. In daily life, density explains everything from why boats float to why air bubbles will try to escape from soda. It even affects your health because bone density is very important. Similarly, percent composition is commonly used to make animal feed and compounds such as the baking soda found in your kitchen.
Density
Density is a physical property found by dividing the mass of an object by its volume. Regardless of the sample size, density is always constant. For example, the density of a pure sample of tungsten is always 19.25 grams per cubic centimeter. This means that whether you have one gram or one kilogram of the sample, the density will never vary. The equation, as we already know, is as follows:
\[ \text{Density} = \dfrac{\text{Mass}}{\text{Volume}} \label{1.5.4}\]
or just
\[\rho = \dfrac{m}{v} \label{1.5.5}\]
Based on this equation, it's clear that density can, and does, vary from element to element and substance to substance due to differences in the relation of mass and volume. But let us break it down one step further. What are mass and volume? We cannot understand density until we know its parts: mass and volume. The following two sections will teach you all the information you need to know about volume and mass to properly solve and manipulate the density equation.
Mass
Mass concerns the quantity of matter in an object. The SI unit for mass is the kilogram (kg), although grams (g) are commonly used in the laboratory to measure smaller quantities. Often, people mistake weight for mass. Weight concerns the force exerted on an object as a function of mass and gravity. This can be written as
\[\text{Weight} = \text{mass} \times \text{gravity} \label{1.5.6}\]
\(Weight = {m}{g} \label{1.5.7}\)
Since on the earth, the \(g\) in the equation is equal to one, weight and mass are considered equal on earth. It is important to note that although \(g\) is equal to one in basic equations, it actually differs throughout earth by a small fraction depending on location; gravity at the equator is less than at the poles. On other astronomical objects, gravity and hence weight, highly differs. This is because weight changes due to variations in gravity and acceleration. The mass, however, of a 1 kg cube will continue to be 1 kg whether it is on the top of a mountain, the bottom of the sea, or on the moon.
Another important difference between mass and weight is how they are measured. Weight is measured with a scale, while mass must be measured with a balance. Just as people confuse mass and weight, they also confuse scales and balances. A balance counteracts the effects of gravity while a scale incorporates it. There are two types of balances found in the laboratory: electronic and manual. With a manual balance, you find the unknown mass of an object by adjusting or comparing known masses until equilibrium is reached. With an electronic balance, which is what you will work with in the UC Davis laboratory, the mass is found by electronic counterbalancing with little effort from the user. An electronic balance can be far more accurate than any other balance and is easier to use, but they are expensive. Also, keep in mind that all instruments used in the laboratory have systematic errors.
Volume
Volume describes the quantity of three dimensional space than an object occupies. The SI unit for volume is meters cubed (m3), but milliliters (mL), centimeters cubed (cm3), and liters (L) are more common in the laboratory. There are many equations to find volume. Here are just a few of the easy ones:
Volume = (length)3
or
Volume = (length)(width)(height)
or
Volume = (base area)(height)
Density: A Further Investigation
Units
We know all of density's components, so let's take a closer look at density itself. The unit most widely used to express density is g/cm3 or g/mL, though the SI unit for density is technically kg/m3. Grams per centimeter cubed is equivalent to grams per milliliter (g/cm3 = g/mL). To solve for density, simply follow the equation 1.5.1. For example, if you had a metal cube with mass 7.0 g and volume 5.0 cm3, the density would be \(\rho = \frac{7\; g}{5\;cm^3}= 1.4\; g/cm^3\). Sometimes, you have to convert units to get the correct units for density, such as mg to g or in3 to cm3.
Density in the Periodic Table
Density can be used to help identify an unknown element. Of course, you have to know the density of an element with respect to other elements. Below is a table listing the density of a few elements from the Periodic Table at standard conditions for temperature and pressure, or STP. STP corresponds to a temperature of 273 K (0° Celsius) and 1 atmosphere of pressure.
| Element Name and Symbol | Density (g/cm3) | Atomic Number |
|---|---|---|
| Hydrogen (H) | 0.09 | 1 |
| Helium (He) | 0.18 | 2 |
| Aluminum (Al) | 2.7 | 13 |
| Zinc (Zn) | 7.13 | 30 |
| Tin (Sn) | 7.31 | 50 |
| Iron (Fe) | 7.87 | 26 |
| Nickel (Ni) | 8.9 | 28 |
| Cobalt (Co) | 8.9 | 27 |
| Copper (Cu) | 8.96 | 29 |
| Silver (Ag) | 10.5 | 47 |
| Lead (Pb) | 11.35 | 82 |
| Mercury (Hg) | 11.55 | 80 |
| Gold (Au) | 19.32 | 79 |
| Platinum (Pt) | 21.45 | 78 |
| Osmium (Os) | 22.6 | 76 |
As can be seen from the table, the most dense element is Osmium (Os) with a density of 22.6 g/cm3. The least dense element is Hydrogen (H) with a density of 0.09 g/cm3.
Density and Temperature
Density generally decreases with increasing temperature and likewise increases with decreasing temperatures. This is because volume differs according to temperature. Volume increases with increasing temperature. Below is a table showing the density of pure water with differing temperatures.
| Temperature (C) | Density (g/cm3) |
|---|---|
| 100 | 0.9584 |
| 80 | 0.9718 |
| 60 | 0.9832 |
| 40 | 0.9922 |
| 30 | 0.9957 |
| 25 | 0.997 |
| 22 | 0.9978 |
| 20 | 0.9982 |
| 15 | 0.9991 |
| 10 | 0.9997 |
| 4 | 1.000 |
| 0 (liquid) | 0.9998 |
| 0 (solid) | 0.9150 |
As can be seen from Table \(\PageIndex{2}\), the density of water decreases with increasing temperature. Liquid water also shows an exception to this rule from 0 degrees Celsius to 4 degrees Celsius, where it increases in density instead of decreasing as expected. Looking at the table, you can also see that ice is less dense than water. This is unusual as solids are generally denser than their liquid counterparts. Ice is less dense than water due to hydrogen bonding. In the water molecule, the hydrogen bonds are strong and compact. As the water freezes into the hexagonal crystals of ice, these hydrogen bonds are forced farther apart and the volume increases. With this volume increase comes a decrease in density. This explains why ice floats to the top of a cup of water: the ice is less dense.
Even though the rule of density and temperature has its exceptions, it is still useful. For example, it explains how hot air balloons work.

Density and Pressure
Density increases with increasing pressure because volume decreases as pressure increases. And since density=mass/volume , the lower the volume, the higher the density. This is why all density values in the Periodic Table are recorded at STP, as mentioned in the section "Density and the Periodic Table." The decrease in volume as related to pressure is explained in Boyle's Law: \(P_1V_1 = P_2V_2\) where P = pressure and V = volume. This idea is explained in the figure below.

Archimedes' Principle
The Greek scientist Archimedes made a significant discovery in 212 B.C. The story goes that Archimedes was asked to find out for the King if his goldsmith was cheating him by replacing his gold for the crown with silver, a cheaper metal. Archimedes did not know how to find the volume of an irregularly shaped object such as the crown, even though he knew he could distinguish between elements by their density. While meditating on this puzzle in a bath, Archimedes recognized that when he entered the bath, the water rose. He then realized that he could use a similar process to determine the density of the crown! He then supposedly ran through the streets naked shouting "Eureka," which means "I found it!" in Latin.
Archimedes then tested the king's crown by taking a genuine gold crown of equal mass and comparing the densities of the two. The king's crown displaced more water than the gold crown of the same mass, meaning that the king's crown had a greater volume and thus had a smaller density than the real gold crown. The king's "gold" crown, therefore, was not made of pure gold. Of course, this tale is disputed today because Archimedes was not precise in all his measurements, which would make it hard to determine accurately the differences between the two crowns.
Archimedes' Principle states that if an object has a greater density than the liquid that it is placed into, it will sink and displace a volume of liquid equal to its own. If it has a smaller density, it will float and displace a mass of liquid equal to its own. If the density is equal, it will not sink or float (Figure \(\PageIndex{2}\)). The principle explains why balloons filled with helium float. Balloons, as we learned in the section concerning density and temperature, float because they are less dense than the surrounding air. Helium is less dense than the atmospheric air, so it rises. Archimedes' Principle can also be used to explain why boats float. Boats, including all the air space, within their hulls, are far less dense than water. Boats made of steel can float because they displace their mass in water without submerging all the way. The table below gives the densities of a few liquids to put things into perspective.
| Liquid |
Density in kg/m3
|
Density in g/cm3 |
|---|---|---|
| 2-Methoxyethanol |
964.60
|
0.9646 |
| Acetic Acid |
1049.10
|
1.049 |
| Acetone |
789.86
|
0.7898 |
| Alcohol, ethyl |
785.06
|
0.7851 |
| Alcohol, methyl |
786.51
|
0.7865 |
| Ammonia |
823.35
|
0.8234 |
| Benzene |
873.81
|
0.8738 |
| Water, pure |
1000.00
|
1.000 |
Percent Composition
Percent composition is very simple. Percent composition tells you by mass what percent of each element is present in a compound. A chemical compound is the combination of two or more elements. If you are studying a chemical compound, you may want to find the percent composition of a certain element within that chemical compound. The equation for percent composition is
\[\text{Percent Composition} = \dfrac{\text{Total mass of element present}}{\text{Molecular mass}} \times 100\% \label{1.5.3}\]
If you want to know the percent composition of the elements in an compound, follow these steps:
Steps to Solve:
- Find the molar mass of all the elements in the compound in grams per mole.
- Find the molecular mass of the entire compound.
- Divide the component's molar mass by the entire molecular mass.
- You will now have a number between 0 and 1. Multiply it by 100 to get percent composition!
Tips for solving:
- The compounds will always add up to 100%, so in a binary compound, you can find the % of the first element, then do 100%-(% first element) to get (% second element)
- If using a calculator, you can store the overall molar mass to a variable such as "A". This will speed up calculations, and reduce typographical errors.
These steps are outlined in the figure below.

For another example, if you wanted to know the percent composition of hydrochloric acid (HCl), first find the molar mass of Hydrogen. H = 1.00794g. Now find the molecular mass of HCl: 1.00794g + 35.4527g = 36.46064g. Follow steps 3 and 4: (1.00794g/36.46064g) x 100 = 2.76% Now just subtract to find the percent by mass of Chlorine in the compound: 100%-2.76% = 97.24% Therefore, HCl is 2.76% Hydrogen and 97.24% Chlorine by mass.
Percent Composition in Everyday Life
Percent composition plays an important role in everyday life. It is more than just the amount of chlorine in your swimming pool because it concerns everything from the money in your pocket to your health and how you live. The next two sections describe percent composition as it relates to you.
The nutrition label found on the container of every bit of processed food sold by the local grocery store employs the idea of percent composition. On all nutrition labels, a known serving size is broken down in five categories: Total Fat, Cholesterol, Sodium, Total Carbohydrate, and Protein. These categories are broken down into further subcategories, including Saturated Fat and Dietary Fiber. The mass for each category, except Protein, is then converted to percent of Daily Value. Only two subcategories, Saturated Fat and Dietary Fiber are converted to percent of Daily Value. The Daily Value is based on a the mass of each category recommended per day per person for a 2000 calorie diet. The mass of protein is not converted to percent because their is no recommended daily value for protein. Following is a picture outlining these ideas.
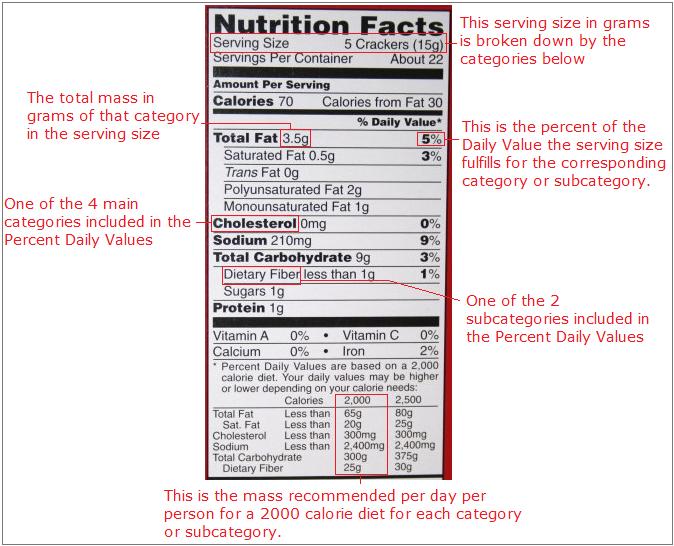
For example, if you wanted to know the percent by mass of the daily value for sodium you are eating when you eat one serving of the food with this nutrition label, then go to the category marked sodium. Look across the same row and read the percent written. If you eat one serving of this food, then you will have consumed about 9% of your daily recommended value for sodium. To find the percent mass of fat in the whole food, you could divide 3.5 grams by 15 grams, and see that this snack is 23.33% fat.
The penny should be called "the lucky copper coated coin." The penny has not been made of solid copper since part of 1857. After 1857, the US government started adding other cheaper metals to the mix. The penny, being only one cent, is literally not worth its weight in copper. People could melt copper pennies and sell the copper for more than the pennies were worth. After 1857, nickel was mixed with the more expensive copper. After 1864, the penny was made of bronze. Bronze is 95% copper and 5% zinc and tin. For one year, 1943, the penny had no copper in it due to the expense of the World War II. It was just zinc coated steel. After 1943 until 1982, the penny went through periods where it was brass or bronze.

The percent composition of a penny may actually affect health, particularly the health of small children and pets. Since the newer pennies are made mainly of zinc instead of copper, they are a danger to a child's health if ingested. Zinc is very susceptible to acid. If the thin copper coating is scratched and the hydrochloric acid present in the stomach comes into contact with the zinc core it could cause ulcers, anemia, kidney and liver damage, or even death in severe cases. Three important factors in penny ingestion are time, pH of the stomach, and amount of pennies ingested. Of course, the more pennies swallowed, the more danger of an overdose of zinc. The more acidic the environment, the more zinc will be released in less time. This zinc is then absorbed and sent to the liver where it begins to cause damage. In this kind of situation, time is of the essence. The faster the penny is removed, the less zinc is absorbed. If the penny or pennies are not removed, organ failure and death can occur.
Below is a picture of a scratched penny before and after it had been submerged in lemon juice. Lemon juice has a similar pH of 1.5-2.5 when compared to the normal human stomach after food has been consumed. Time elapsed: 36 hours.


As you can see, the copper is vastly unharmed by the lemon juice. That's why pennies made before 1982 with mainly copper (except the 1943 penny) are relatively safe to swallow. Chances are they would pass through the digestive system naturally before any damage could be done. Yet, it is clear that the zinc was partially dissolved even though it was in the lemon juice for only a limited amount of time. Therefore, the percent composition of post 1982 pennies is hazardous to your health and the health of your pets if ingested.
Problems
Following are examples of different types of percent composition and density problems.
Density Problems: These problems are meant to be easy in the beginning and then gradually become more challenging. Unless otherwise stated, answers should be in g/mL or the equivalent g/cm3.
- If you have a 2.130 mL sample of acetic acid with mass 0.002234 kg, what is the density?
- Calculate the density of a .03020 L sample of ethyl alcohol with a mass of 23.71002 g.
- Find the density of a sample that has a volume of 36.5 L and a mass of 10.0 kg.
- Find the volume in mL of an object that has a density of 10.2 g/L and a mass of 30.0 kg.
- Calculate the mass in grams of an object with a volume of 23.5 mL and density of 10.0 g/L.
- Calculate the density of a rectangular prism made of metal. The dimensions of the prism are: 5 cm by 4 cm by 5 cm. The metal has a mass of 50 grams.
- Find the density of an unknown liquid in a beaker. The beaker's mass is 165 g when there is no liquid present. With the unknown liquid, the total mass is 309 g. The volume of the unknown is 125 mL.
- Determine the density in g/L of an unknown with the following information. A 55 gallon tub weighs 137.5lb when empty and 500.0 lb when filled with the unknown.
- A ring has a mass of 5.00g and a volume of 0.476 mL. Is it pure silver?
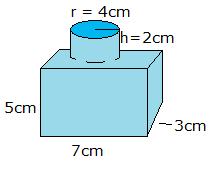
- What is the density of the solid in the image if the mass is 40 g? Make your answer have 3 significant figures.
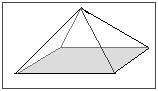
- Below is a model of a pyramid found at an archeological dig made of an unknown substance. It is too large to find the volume by submerging it in water. Also, the scientists refuse to remove a piece to test because this pyramid is a part of history. Its height is 150.0m. The length of its base is 75.0m and the width is 50.0m. The mass of this pyramid is 5.50x105kg. What is the density?
Percent Composition Problems: These problems will follow the same pattern of difficulty as those of density.
- Calculate the percent by mass of each element in Cesium Fluoride (CsF).
- Calculate the percent by mass of each element present in carbon tetrachloride (CCl4)
- A solution of salt and water is 33.0% salt by mass and has a density of 1.50 g/mL. What mass of the salt in grams is in 5.00L of this solution?
- A solution of water and HCl contains 25% HCl by mass. The density of the solution is 1.05 g/mL. If you need 1.7g of HCl for a reaction, what volume of this solution will you use?
- A solution containing 42% NaOH by mass has a density of 1.30 g/mL. What mass, in kilograms, of NaOH is in 6.00 L of this solution?
Answers
Here are the solutions to the listed practice problems.
Density Problem Solutions
- 1.049 g/mL
- 0.7851 g/mL
- 0.274 g/mL
- 2.94 x 106 mL
- 0.3.27 kg
- 0.5 g/cm3
- 1.15 g/mL
- 790 g/L
- Yes
- 0.195 g/cm3
- 29.3 g/cm3
Percent Composition Problem Solutions
- CsF is 87.5% Cs and 12.5% F by mass
- CCl4 is 92.2% Cl and 7.8% C by mass
- 2480 g
- 6.5 mL
- 3.26 kg
References
- AUTOR , ARQUIMEDES , and Thomas Little . The Works of Archimedes . Courier Dover Publications, 2002.
- Chande, D. and T. Fisher (2003). "Have a Penny? Need a Penny? Eliminating the One-Cent Coin from Circulation." Canadian Public Policy/Analyse de Politiques 29(4): 511-517.
-
Jefferson, T. (1999). "A Thought for Your Pennies." JAMA 281(2): 122.
- Petrucci , Ralph , William Harwood , and Geoffrey Herring . Principles and Modern Application. ninth . New Jersey : Peason Eduation , 2007.
-
Rauch, F., H. Plotkin, et al. (2003). "Bone Mass, Size, and Density in Children and Adolescents with Osteogenesis Imperfecta: Effect of Intravenous Pamidronate Therapy." Journal of Bone and Mineral Research 18: 610-614.
-
Richardson, J., S. Gwaltney-Brant, et al. (2002). "Zinc Toxicosis from Penny Ingestion in Dogs." Vet Med 97(2): 96-99.
-
Tate, J. "Archimedes’ Discoveries: A Closer Look."

