1.1: Chemistry and it's Methods
- Page ID
- 13572
John Dalton (1766-1844) is the scientist credited for proposing the atomic theory. This theory explains several concepts that are relevant in the observable world: the composition of a pure gold necklace, what makes the pure gold necklace different than a pure silver necklace, and what occurs when pure gold is mixed with pure copper. Before discussing the atomic theory, this article explains the theories that Dalton used as a basis for his theory: the law of conservation of mass and the law of constant composition.
Law of Conservation of Mass: (1766-1844)
The law of conservation of mass states that the total mass present before a chemical reaction is the same as the total mass present after the chemical reaction; in other words, mass is conserved. The law of conservation of mass was formulated by Antoine Lavoisier (1743-1794) as a result of his combustion experiment, in which he observed that the mass of his original substance—a glass vessel, tin, and air—was equal to the mass of the produced substance—the glass vessel, “tin calx”, and the remaining air.
Historically, this was a difficult concept for scientists to grasp. If this law was true, then how could a large piece of wood be reduced to a small pile of ashes? The wood clearly has a greater mass than the ashes. From this observation scientists concluded that mass had been lost. However, the illustration below shows that the burning of word does follow the law of conservation of mass. Scientists did not take into account the gases that play a critical role in this reaction.
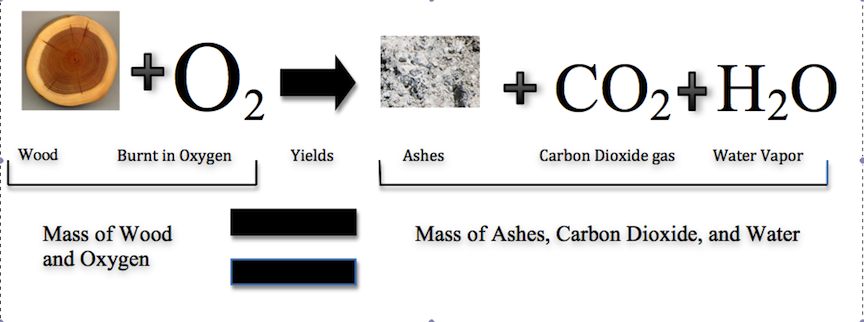
Law of Constant Composition
Joseph Proust (1754-1826) formulated the law of constant composition (also called the law of definite proportions). This law states that if a compound is broken down into its constituent elements, the masses of the constituents will always have the same proportions, regardless of the quantity or source of the original substance. Joseph Proust based this law primarily on his experiments with basic copper carbonate. The illustration below depicts this law; 31 grams of H2O and 8 grams of H2O are made up of the same percent of hydrogen and oxygen.

Dalton's Atomic Theory
1. Each chemical element is composed of extremely small particles that are indivisible and cannot be seen by the naked eye, called atoms. Atoms can neither be created nor destroyed. Pictured below is a helium atom. The purple and red dots represent the neutrons and protons in the nucleus. The black area around the nucleus represent the electron cloud. The following sections discuss this further.
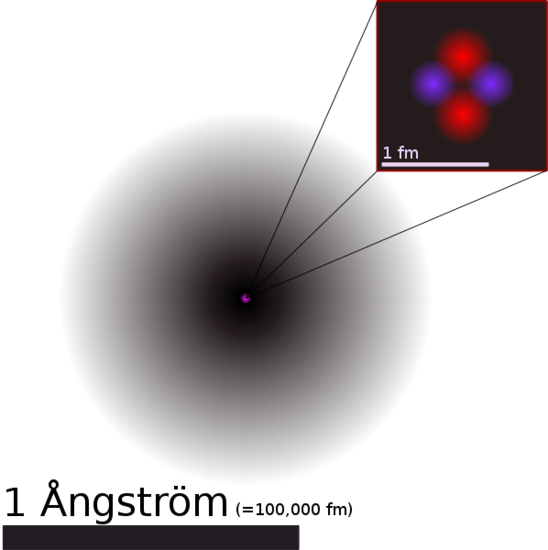
2. All atoms of an element are alike in mass and other properties, but the atoms of one element differ from all other elements. For example, gold and silver have different atomic masses and different properties.


Gold Silver
Atomic Mass: 196.97 Atomic Mass: 107.87
Figure 4 (Gold): Courtesy of Chris Ralph that released this image into the public domain. Figure 5 (silver): Courtesy of resourcescommittee.house.gov/.../photogallery/
3. For each compound, different elements combine in a simple numerical ratio. The illustration below describes this rule. The second equation for the reaction is incorrect because half of an atom does not exist.
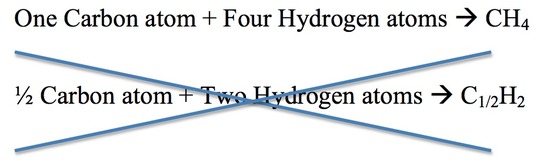
Atomic theory can be used to answers the questions presented above. A pure gold necklace is made up of atoms. A pure gold necklace and a pure silver necklace are different because they have different atoms. Pure gold mixed with pure copper forms rose gold. The gold and copper atoms combine in a simple numerical ratio.
Dalton's theory has not proven to be correct under all circumstances. The first rule was proven incorrect when scientists divided atoms in a process called nuclear fission. The second rule was proven incorrect by the discovery that not all atoms of the same element have the same mass; there are different isotopes. However, these failures do not justify discarding the atomic theory. It correctly explains the law of conservation of mass: if atoms of an element are indestructible, then the same atom must be present after a chemical reaction as before and, and the mass must constant. Dalton’s atomic theory also explains the law of constant composition: if all the atoms of an element are alike in mass and if atoms unite in fixed numerical ratios, the percent composition of a compound must have a unique value without regards to the sample analyzed. The atomic theory led to the creation of the law of multiple proportions.
Law of Multiple Proportions
The law of multiple proportions states that if two elements form more than one compound between them, the masses of one element combined with a fixed mass of the second element form in ratios of small integers. The illustration of the third rule of the atomic theory correctly depicts this law.
Discovering Electrons
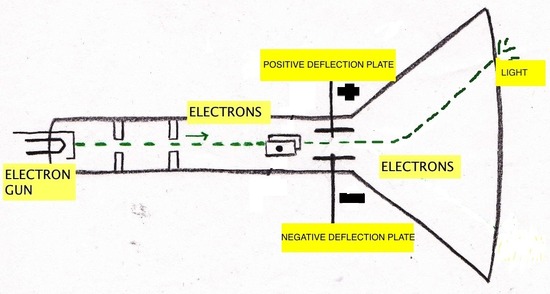
The first cathode-ray tube (CRT) was invented by Michael Faraday (1791-1867). Cathode rays are a type of radiation emitted by the negative terminal, the cathode, and were discovered by passing electricity through nearly-evacuated glass tubes. The radiation crosses the evacuated tube to the positive terminal, the anode. Cathode rays produced by the CRT are invisible and can only be detected by light emitted by the materials that they strike, called phosphors, painted at the end of the CRT to reveal the path of the cathode rays. These phosphors showed that cathode rays travel in straight lines and have properties independent of the cathode material (whether it is gold, silver, etc.). Another significant property of cathode rays is that they are deflected by magnetic and electric fields in a manner that is identical to negatively charged material. Due to these observations, J.J. Thompson (1856-1940) concluded that cathode rays are negatively charged particles that are located in all atoms. It was George Stoney who first gave the term electrons to the cathode rays. The below figures depict the way that the cathode ray is effected by magnetics. The cathode ray is always attracted by the positive magnet and deflected by the negative magnets.
The Plum Pudding Model
After Thompson discovered the electron, he proposed the plum pudding model of an atom, which states that the electrons float in positively-charged material. This model was named after the plum-pudding dessert.

Discovery of the Proton
In 1909, Ernest Rutherford (1871-1937) performed a series of experiments studying the inner structure of atoms using alpha particles. Rutherford knew that alpha particles are significantly more massive than electrons and positively charged. Using the plum-pudding model for reference, Rutherford predicted that particles in an alpha beam would largely pass through matter unaffected, with a small number of particles slightly deflected. The particles would only be deflected if they happened to come into contact with electrons. According to the plum pudding model, this occurrence would be very unlikely. In order to test his hypothesis, Rutherford shot a beam of alpha particles at a thin piece of gold foil. Around the gold foil Rutherford placed sheets of zinc sulfide. These sheets produced a flash of light when struck by an alpha particle. However, this experiment produced results that contradicted Rutherford's hypothesis. Rutherford observed that the majority of the alpha particles went through the foil; however, some particles were slightly deflected, a small number were greatly deflected, and another small number were thrown back in nearly the direction from which they had come. Figure 10 shows Rutherford's prediction based off of the plum-pudding model (pink) and the observed large deflections of the alpha particles (gold).
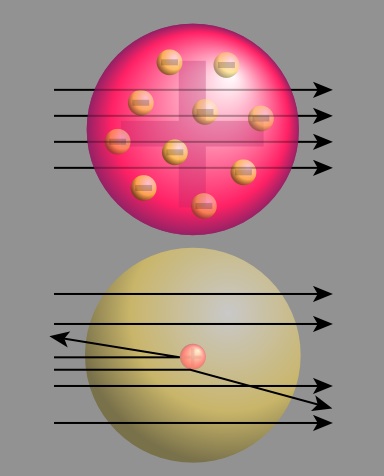
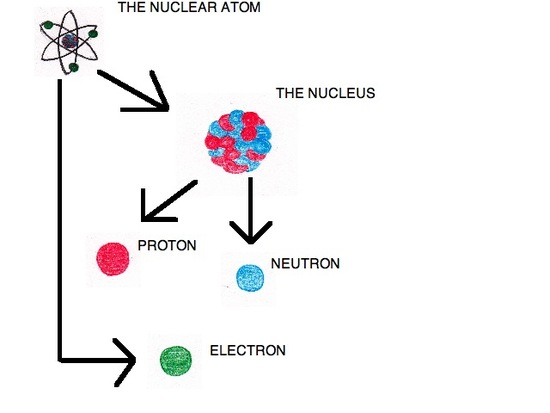
To account for these observations, Rutherford devised a model called the nuclear atom. In this model, the positive charge is held in an extremely small area called the nucleus, located in the middle of the atom. Outside of the nucleus the atom is largely composed of empty space. This model states that there were positive particles within the nucleus, but failed to define what these particles are. Rutherford discovered these particles in 1919, when he conducted an experiment that scattered alpha particles against nitrogen atoms. When the alpha particles and nitrogen atoms collided protons were released.
The Discovery of the Neutron
In 1933, James Chadwick (1891-1974) discovered a new type of radiation that consisted of neutral particles. It was discovered that these neutral atoms come from the nucleus of the atom. This last discovery completed the atomic model.
Example Problems
1. Basic concept check: When 32.0 grams (g) of methane are burned in 128.0 g of oxygen, 88.0 g of carbon dioxide and 72.0 g of water are produced. Which law is this an example of? (a) Law of Definite Proportions (b) Law of Conservation of Mass or (c) Law of Multiple Proportions.
The answer is (b) Law of Conservation of Mass. The number of grams of reactants (32.0 g of methane and 128.0 g of oxygen = 160.0 g total) is equal to the number of grams of product (88.0 g of carbon dioxide and 72.0 g of water = 160.0 g total).
2. Law of Conservation of Mass: 8.00 grams (g) of methane are burned in 32.00 g of oxygen. The reaction produces 22.00 g of carbon dioxide and an unmeasured mass of water. What mass of water is produced?
The answer is 18.00 g of water. Because the only products are water and carbon dioxide, their total mass must equal the total mass of the reactants, methane and oxygen. 8.00 g of methane + 32.00 g of oxygen = 40.00 total g of reactants. Because the total mass of the reactants equals the total mass of the products, the total mass of the products is also 40.00 g. Thus, 40.00 total g of products = 22.00 g carbon dioxide + unknown mass water. 40.00 total g of products - 22.00 g carbon dioxide = 18.00 g water.
3. Law of Definite Proportions: Two experiments using sodium and chlorine are performed. In the first experiment, 4.36 grams (g) sodium are reacted with 32.24 g of chlorine, using up all the sodium. 11.08 g of sodium chloride was produced in the first experiment. In the second experiment, 4.20 g of chlorine reacted with 20.00 g of sodium, using up all the chlorine. 6.92 g of of sodium chloride was produced in the second experiment. Show that these results are consistent with the law of constant composition.
To solve, determine the percent of sodium in each sample of sodium chloride. There is 4.36 g sodium for every 11.08 g of sodium chloride in the first experiment. The amount of sodium in the sodium chloride for the second experiment must be found. This is found by subtracted the known amount of reacted chlorine (4.20 g) from the amount of sodium chloride (6.92 g). 6.92 g sodium chloride - 4.20 g chlorine = 2.72 g sodium.
Thus, the percent of sodium in each sample is represented below:
% Na = (4.36 g Na)/(11.08 g NaCl) x 100% = 39.4% Na % Na = (2.72 g Na)/(6.92 g NaCl) x 100% = 39.3%
The slight difference in compositions is due to significant figures: each percent has an uncertainty of .01% in either direction. The two samples of sodium chloride have the same composition.
4. Law of Conservation of Mass: 36.0 grams (g) of wood are burned in oxygen. The products of this reaction weigh 74.4 g. (a) What mass of oxygen is needed in this reaction? (b) What mass of oxygen is needed to burn 8.00 lb of wood? 1 lb = 453.59237 g.
- The answer is 38.4 g of oxygen. The total mass of the products is 74.4 g. Thus, the total mass of the reactants must equal 74.4 g as well. Thus, 74.4 g products - 36.0 g wood reactant = 38.4 g oxygen reactant.
- The answer is 8.53 lb of oxygen. From, (a) that it takes 38.4 g of oxygen to burn 18.0 g of wood. First, convert both of these values to pounds (alternatively, the 8.00 lb can be converted to grams).
36.0 g wood x (1lb)/(453.59237 g) = .0793664144 lb wood
38.4 g oxygen x (1 lb)/(453.59237 g) = .0846575087 lb oxygen
Now two ratios equal to each other can be set up to determine the unknown mass of oxygen.
(0.0793664144 lb wood)/(.0846575087 lb oxygen) = (8.00 lb wood)/(unknown mass oxygen)
Solving reveals that it requires 8.53 lb of oxygen to burn 8.00 lb of wood.
5. Law of Definite Proportions: A sample of methane contains only carbon and hydrogen, with 3.00 grams (g) of carbon for every 1.00 g of hydrogen. How much hydrogen should be present in a different, 50.0 g same of methane?
The answer is 12.5 g of hydrogen. If there are 3.00 g of carbon present for every 1.00 g of hydrogen, we can assume the smallest whole number combination of these elements in that ratio to be 4.00 g of methane:
50.0 g methane x (1.00 g hydrogen)/(4.00 g methane) = 12.5 g of hydrogen.
Outside links
- Description of Atomic Theory - http://en.Wikipedia.org/wiki/Atomic_theory
- Description of Atomic Theory - http://www.visionlearning.com/librar...wer.php?mid=50
- Cathode Ray Demonstration - www.youtube.com/watch?v=XU8nMKkzbT8
- Theoretical Demonstration of Conservation of Mass - www.youtube.com/watch?v=dExpJAECSL8
- Actual Demonstration of Conservation of Mass - www.youtube.com/watch?v=J5hM1...eature=related
- The alpha scattering experiment-http://www.youtube.com/watch?v=5pZj0u_XMbc
References
- Petrucci, Ralph, William Harwood, Geoffrey Herring, and Jeffry Madura. General Chemistry. 9th ed. Upper Saddle River, New Jersey: Pearson Prentince Hall, 2007
- Moore, John. Chemistry for Dummies. John Wiley & Sons Inc, 2002.
- Asimov, Isaac. A Short History of Chemistry. , CT.: Greenwood Press, 1965.
- Patterson, Elizabeth C. John Dalton and the Atomic Theory. Garden City, NY: Doubleday, 1970
- Myers, Richard. The Basics of Chemistry. Greenwood, 2003
- Demtröder, Wolfgang. Atoms, Molecules and Photons: An Introduction to Atomic- Molecular- and Quantum Physics. 1st ed. Springer. 2002

