17.E: Additional Aspects of Aqueous Equilibria (Exercises)
- Last updated
- Save as PDF
- Page ID
- 25254
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)17.2: Buffered Solutions
Conceptual Problems
1. Explain why buffers are crucial for the proper functioning of biological systems.
2. What is the role of a buffer in chemistry and biology? Is it correct to say that buffers prevent a change in \([H_3O^+]\)? Explain your reasoning.
3. Explain why the most effective buffers are those that contain approximately equal amounts of the weak acid and its conjugate base.
4. Which region of the titration curve of a weak acid or a weak base corresponds to the region of the smallest change in pH per amount of added strong acid or strong base?
5. If you were given a solution of sodium acetate, describe two ways you could convert the solution to a buffer.
6. Why are buffers usually used only within approximately one pH unit of the \(pK_a\) or \(pK_b\) of the parent weak acid or base?
7. The titration curve for a monoprotic acid can be divided into four regions: the starting point, the region around the midpoint of the titration, the equivalence point, and the region after the equivalence point. For which region would you use each approach to describe the behavior of the solution?
- a buffer
- a solution of a salt of a weak base
- a solution of a weak acid
- diluting a strong base
8. Which of the following will produce a buffer solution? Explain your reasoning in each case.
- mixing 100 mL of 0.1 M \(HCl\) and 100 mL of 0.1 M sodium fluoride
- mixing 50 mL of 0.1 M \(HCl\) and 100 mL of 0.1 M sodium fluoride
- mixing 100 mL of 0.1 M hydrofluoric acid and 100 mL of 0.1 M \(HCl\)
- mixing 100 mL of 0.1 M hydrofluoric acid and 50 mL of 0.1 M \(NaOH\)
- mixing 100 mL of 0.1 M sodium fluoride and 50 mL of 0.1 M \(NaOH\).
9. Which of the following will produce a buffer solution? Explain your reasoning in each case.
- mixing 100 mL of 0.1 M \(HCl\) and 100 mL of 0.1 M sodium acetate
- mixing 50 mL of 0.1 M \(HCl\) and 100 mL of 0.1 M sodium acetate
- mixing 100 mL of 0.1 M acetic acid and 100 mL of 0.1 M \(NaOH\)
- mixing 100 mL of 0.1 M acetic acid and 50 mL of 0.1 M \(NaOH\)
- mixing 100 mL of 0.1 M sodium acetate and 50 mL of 0.1 M acetic acid
10. Use the definition of Kb for a weak base to derive the following expression, which is analogous to the Henderson-Hasselbalch approximation but for a weak base (B) rather than a weak acid (HA):
11. Why do biological systems use overlapping buffer systems to maintain a constant pH?
12. The \(CO_2/HCO_3^−\) buffer system of blood has an effective \(pK_a\) of approximately 6.1, yet the normal pH of blood is 7.4. Why is \(CO_2/HCO_3^−\) an effective buffer when the \(pK_a\) is more than 1 unit below the pH of blood? What happens to the pH of blood when the \(CO_2\) pressure increases? when the \(O_2\) pressure increases?
13. Carbon dioxide produced during respiration is converted to carbonic acid (\(H_2CO_3\)). The \(pK_a1\) of carbonic acid is 6.35, and its \(pK_a2\) is 10.33. Write the equations corresponding to each pK value and predict the equilibrium position for each reaction.
Answer
1. Buffers are crucial for the proper function of biological systems because they help maintain a relatively constant \(pH\) that maintains homeostasis and this is required for bodily function. For example, buffers can prevent stomach acid from being too acidic in which tissues and other parts of the body would be harmed.
2. The role of a buffer in chemistry and biology is to resist pH changes upon the addition of an acid or base. It is correct to say that buffers prevent a change in hydronium ion concentration because the pH is a measure of the acidity or alkalinity of a solution.
3. The most effective buffers are those that contain approximately equal amounts of the weak acid and its conjugate base because when placed in the Henderson-Hasselbalch equation the \(pH\) approximately equals the \(pK_{a}\). This is the goal because the more the ratio needs to differ to achieve the desired pH, the less effective the buffer and it should not differ by more than tenfold.
4. The region after the equivalence point on a titration curve of a weak acid or a weak base corresponds to the smallest change in pH per amount of added strong acid or strong base. This is because the strong acid or strong base completely neutralized the weak acid or weak base in which the pH remains constant relative to the strong acid or strong base.
5. Sodium acetate is a salt, therefore it can’t be regarded as an acid or a base. One way to convert the solution to a buffer is to combine sodium acetate with a weak acid such as acetic acid. The sodium acetate would react with the hydronium ions and the acetic acid would react with hydroxide ions to prevent drastic changes in pH. Another way to convert the solution to a buffer is by titrating a weak acid and strong base or strong base and weak acid. For example, combining acetic acid to sodium hydroxide to produce sodium acetate (a neutralization reaction).
6.
Buffers are usually used only within approximately one \(pH\) unit of the \(pK_a\) or \(pK_b\) of the parent weak acid or base because the ability of a buffer solution to maintain a nearly constant pH due to a small amount of acid or base is greatest at the \(pK_a\) and decreases as the pH of the solution goes above or below the \(pK_a\).
\(pH=pK_a+log(\frac{[B]}{[A]})\)
When \(\frac{[B]}{[A]}=10\): \(pH=pK_a+1\)
When \(\frac{[B]}{[A]}=\frac{1}{10}\): \(pH=pK_a-1\)
7.
a. I would use the region around the midpoint of the titration to describe the behavior of a buffer because the midpoint of the titration is defined as the point at which exactly enough acid or base has been added to neutralize one-half of the acid or the base originally present while maintaining a relatively constant pH.
b. I would use the equivalence point region to describe the behavior of a solution of a salt of a weak base because at this point the amount of titrant added is enough to completely neutralize the solution.
c. I would use the starting point region of the titration curve to describe the behavior of the solution of a weak acid because it is expected to be at a higher pH than a strong acid but lower than \(pH\) 7.
d. I would use the region after the equivalence point to describe the dilution of a strong base because in this region one can predict the pH by simply taking into account the amount of excess base.
8.
a. This will not produce a buffer solution because the hydrochloric acid completely neutralizes the sodium fluoride to give sodium chloride.
b. This will produce a buffer solution because the hydrochloric acid neutralizes only half of the acetic acid to give a solution containing equal amounts of hydrofluoric acid and sodium chloride.
c. This will not produce a buffer solution because hydrofluoric acid is a weak acid and hydrochloric acid is a strong acid.
d. This will produce a buffer solution because the solution will contain a 2:1 ratio of hydrofluoric acid and sodium hydroxide.
e. This will not produce a buffer solution solution because sodium fluoride is a weak base and sodium hydroxide is a strong base.
9.
a. This will not produce a buffer because the hydrochloric acid completely neutralizes the sodium acetate to give acetic acid and sodium chloride.
b. This will produce a buffer because the HCl neutralizes only half of the sodium acetate to give a solution containing equal amounts of acetic acid and sodium acetate.
c. This will not produce a buffer because the sodium hydroxide completely neutralizes the acetic acid to give sodium acetate.
d. This will produce a buffer because the sodium hydroxide neutralizes only half of the acetic acid to give a solution containing equal amounts of acetic acid and sodium acetate.
e. This will produce a buffer because the solution will contain a 2:1 ratio of sodium acetate and acetic acid.
10.
For \(pH\):
\(HA \overset{K_a}{\rightleftharpoons} A^{-}+H^{+}\)
\(K_a= \frac{[H^{+}][A^{-}]}{[HA]}\)
\(log(K_a)=log([H^{+}])+log(\frac{[A^{-}]}{[HA]})\)
\(-pK_a=-pH+log(\frac{[A^{-}]}{[HA]})\)
\(pH=pK_a+log(\frac{[A^{-}]}{[HA]})\)
For pOH:
\(A^{-} \overset{K_b}{\rightleftharpoons} HA+OH^{-}\)
\(K_b= \frac{[HA][OH^{-}]}{[A^{-}]}\)
\(log(K_b)=log([OH^{-}])+log(\frac{[HA]}{[A^{-}]})\)
\(-pK_b=-pOH-log(\frac{[A^{-}]}{[HA]})\)
\(pOH=pK_b-log(\frac{[A^{-}]}{[HA]})\)
Helpful Equations:
\(pK_a=-log(K_a) \rightarrow -pK_a=log(K_a)\)
\(-log([H^{+}])=pH \rightarrow log([H^{+}])=-pH\)
\(pK_b=-log(K_b) \rightarrow -pK_a=log(K_b)\)
\(-log([OH^{-}])=pOH \rightarrow log([OH^{-}])=-pOH\)
11. Biological systems use overlapping buffer systems to maintain a constant pH because no single buffer system can effectively maintain a constant pH value over the entire physiological range of approximately \(pH\) 5.0 to 7.4.
12. \(CO_2/HCO_3^−\) is an effective buffer when the \(pK_a\) is more than 1 unit below the \(pH\) of blood because the kidneys help control acid-base balance by excreting hydrogen ions and generating bicarbonate that helps maintain blood plasma \(pH\) within the normal range. The bicarbonate ion can combine with a proton to form carbonic acid and the more protons are absorbed from the solution the more the \(pH\) increases, resulting in hemoglobin absorbing oxygen. Carbonic acid, which can be formed from carbon dioxide and water, can dissociate into a proton and bicarbonate ion which increases the hydrogen ion concentration and lowers the blood \(pH\), resulting in hemoglobin proteins releasing oxygen. The carbonic acid, which can be formed from bicarbonate, is converted to carbon dioxide and water via a very fast enzymatic reaction. Carbon dioxide, being volatile, can be rapidly expelled from the body at varying rates by respiration.
13.
\(H_{2}CO_{3} \rightleftharpoons HCO_{3}^{-}+H^{+}\) \(pK_{a1}=6.35\) left
\(HCO_{3}^{-} \rightleftharpoons CO_{3}^{2-}+H^{+}\) \(pK_{a2}=10.33\) right
Numerical Problems
1.Benzenesulfonic acid (\(pKa = 0.70\)) is synthesized by treating benzene with concentrated sulfuric acid. Calculate the following:
- the \(pH\) of a 0.286 M solution of benzenesulfonic acid
- the pH after adding enough sodium benzenesulfonate to give a final benzenesulfonate concentration of 0.100 M
2. Phenol has a \(pK_a\) of 9.99. Calculate the following:
- the \(pH\) of a 0.195 M solution
- the percent increase in the concentration of phenol after adding enough solid sodium phenoxide (the sodium salt of the conjugate base) to give a total phenoxide concentration of 0.100 M
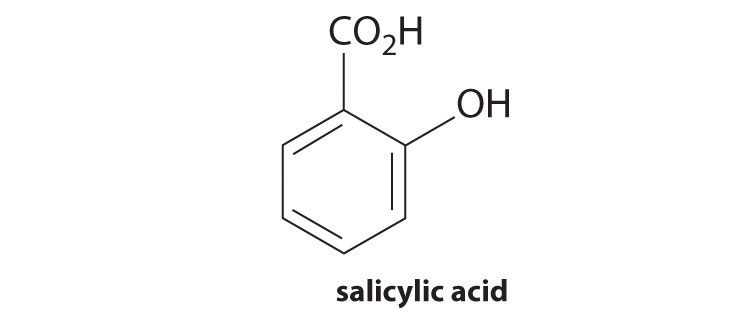
3. Salicylic acid is used in the synthesis of acetylsalicylic acid, or aspirin. One gram dissolves in 460 mL of water to create a saturated solution with a \(pH\) of 2.40.
- What is the \(K_a\) of salicylic acid?
- What is the final pH of a saturated solution that is also 0.238 M in sodium salicylate?
- What is the final pH if 10.00 mL of 0.100 M HCl are added to 150.0 mL of the buffered solution?
- What is the final pH if 10.00 mL of 0.100 M NaOH are added to 150.0 mL of the buffered solution?
4. An intermediate used in the synthesis of perfumes is valeric acid, also called pentanoic acid. The \(pK_a\) of pentanoic acid is 4.84 at 25°C.
- What is the \(pH\) of a 0.259 M solution of pentanoic acid?
- Sodium pentanoate is added to make a buffered solution. What is the pH of the solution if it is 0.210 M in sodium pentanoate?
- What is the final \(pH\) if 8.00 mL of 0.100 M HCl are added to 75.0 mL of the buffered solution?
- What is the final \(pH\) if 8.00 mL of 0.100 M NaOH are added to 75.0 mL of the buffered solution?
Answer
1.
a. \(pH=-log([H^{+}])=-log(0.2388)=0.62\)
\(K_a=\frac{[H^{+}][A^{-}]}{[HA]} \rightarrow K_a=\frac{[H^{+}]^{2}}{[HA]} \rightarrow [H^{+}]= \sqrt{K_a\times[HA]}=\sqrt{10^{-0.70} \times 0.286\,M}=0.2388\)
b. \(pH=-log([H^{+}])=-log(0.14125)=0.850\)
\(K_a=\frac{[H^{+}][A^{-}]}{[HA]} \rightarrow K_a=\frac{[H^{+}]^{2}}{[HA]} \rightarrow [H^{+}]= \sqrt{K_a\times[HA]}=\sqrt{10^{-0.70} \times 0.100\,M}=0.14125\)
2.
a. \(pH=-log(4.46 \times 10^{-6})=5.35\)
\(K_a=\frac{[C_6H_5O^{-}][H_3O^{+}]}{[C_6H_5OH]}=\frac{x^2}{0.195} \rightarrow 10^{-9.99}=\frac{x^2}{0.195} \rightarrow x=4.46 \times 10^{-6}\)
\(Assumption\,Valid: \frac{4.46 \times 10^{-6}}{0.195\,M} \times 100 \% <5 \%\)
|
\(C_6H_5OH\) |
\(H_2O\) |
\(C_6H_5O^{-}\) |
\(H_3O^{+}\) |
|
|
I |
0.195 |
- |
0 |
0 |
|
C |
-x |
- |
+x |
+x |
|
E |
0.195-x |
- |
x |
x |
b. \(Percent\,increase=\frac{3.20 \times 10^{-6}}{4.46 \times 10^{-6}}x100 \% =71.6 \% \)
\(K_a=\frac{[C_6H_5O^{-}][H_3O^{+}]}{C_6H_5OH}=\frac{x^2}{0.100} \rightarrow 10^{-9.99}=\frac{x^2}{0.100} \rightarrow x=3.20 \times 10^{-6}\)
3.
-
\(K_a=\frac{[C_9H_8O_4][H_3O^{+}]}{[C_7H_6O_3]}=\frac{x^{2}}{0.015739} \rightarrow \frac{(3.98 \times 10^{-3})^{2}}{0.015739}= 1.0 \times 10^{-3}\)
\(C_{7}H_{6}O_{3}:1\,g \times \frac{1\,mol}{138.121\,g\,mol} \times \frac{1}{460\,mL \times \frac {1\,L}{1000\,mL}}=0.015739\,M\)
\(pH=-log([H^{+}]) \rightarrow [H^{+}]=10^{-pH}=10^{-2.40}=3.98 \times 10^{-3}\)
-
\(pH=pK_a+log(\frac{[C_{7}H_{5}NaO_{3}]}{[C_{7}H_{6}O_{3}]})=-log(1.01 \times 10^{-3})+log(\frac{0.238}{0.015739})=4.17\)
-
\(pH=pK_a+log(\frac{mol\,C_{7}H_{5}NaO_{3}-mol\,HCl}{mol\,C_9H_8O_4+mol\,HCl})=-log(1.01 \times 10^{-3})+log(\frac{0.0357-0.001}{0.00236085+0.001})=4.01\)
\(HCl:.01\,L \times 0.100\,M=0.001\,mol\)
\(C_{7}H_{5}NaO_{3}: 0.15\,L \times 0.238\,M=0.0357\,mol\)
\(C_{7}H_{6}O_{3}:0.15\,L \times 0.015739\,M=0.00236085\,mol\)
-
\(pH=pK_a+log(\frac{mol\,C_{7}H_{5}NaO_{3}+mol\,NaOH}{mol\,C_9H_8O_4-mol\,NaOH})=-log(1.01 \times 10^{-3})+log(\frac{0.0357+0.001}{0.00236085-0.001})=4.43\)
\(NaOH:.01\,L \times 0.100\,M=0.001\,mol\)
\(C_{7}H_{5}NaO_{3}: 0.15\,L \times 0.238\,M=0.0357\,mol\)
\(C_{7}H_{6}O_{3}:0.15\,L \times 0.015739\,M=0.00236085\,mol\)
4.
a. \(pH=-log([H^{+}])=-log(3.7 \times 10^{-6})=5.43\)
\(K_a=\frac{[H^{+}][A^{-}]}{[HA]} \rightarrow K_a=\frac{[H^{+}]^{2}}{[HA]} \rightarrow [H^{+}]=\sqrt{K_a\times[HA]}=\sqrt{10^{-4.84} \times 0.259\,M}=3.7 \times 10^{-6}\)
b. \(pH=pK_a+log(\frac{B}{A})=4.84+log(\frac{0.210}{0.259})=4.75\)
c. \(pH=pK_a+log(\frac{B}{A})=4.84+log(\frac{mol\,C_{5}H_{9}NaO_{2}-mol\,HCl}{mol\,C_{5}H_{10}O_{2}+mol\,HCl})=4.84+log(\frac{0.01575-8 \times 10^{-4}}{0.019425+8\times 10^{-4}})=4.71\)
\(HCl:8.00\,mL \times \frac{1\,L}{1,000\,mL} \times 0.100\,M=8 \times 10^{-4}\,mol\)
\(C_{5}H_{9}NaO_{2}:75.0\,mL \times \frac{1\,L}{1,000\,mL} \times 0.210\,M=0.01575\,mol\)
\(C_{5}H_{10}O_{2}: 75.0 \,mL \times \frac{1\,L}{1,000\,mL} \times 0.259\,M=0.019425\,mol\)
d. \(pH=pK_a+log(\frac{B}{A})=4.84+log(\frac{mol\,C_{5}H_{9}NaO_{2}+mol\,NaOH}{mol\,C_{5}H_{10}O_{2}-mol\,NaOH})=4.84+log(\frac{0.01575+8 \times 10^{-4}}{0.019425-8\times 10^{-4}})=6.07\)
\(NaOH:8.00\,mL \times \frac{1\,L}{1,000\,mL} \times 0.100\,M=8 \times 10^{-4}\,mol\)
\(C_{5}H_{9}NaO_{2}:75.0\,mL \times \frac{1\,L}{1,000\,mL} \times 0.210\,M=0.01575\,mol\)
\(C_{5}H_{10}O_{2}: 75.0 \,mL \times \frac{1\,L}{1,000\,mL} \times 0.259\,M=0.019425\,mol\)
17.3: Acid-Base Titrations
Conceptual Problems
1. Why is the portion of the titration curve that lies below the equivalence point of a solution of a weak acid displaced upward relative to the titration curve of a strong acid? How are the slopes of the curves different at the equivalence point? Why?
2. Predict whether each solution will be neutral, basic, or acidic at the equivalence point of each titration.
- An aqueous solution of \(NaOH\) is titrated with 0.100 M \(HCl\).
- An aqueous solution of ethylamine (\(CH_3CH_2NH_2\)) is titrated with 0.150 M \(HNO_{3}\)
- An aqueous solution of aniline hydrochloride (\(C_6H_5NH_3^+Cl^−\)) is titrated with 0.050 M \(KOH\).
3. The pKa values of phenol red, bromophenol blue, and phenolphthalein are 7.4, 4.1, and 9.5, respectively. Which indicator is best suited for each acid–base titration?
- titrating a solution of \(Ba(OH)_2\) with 0.100 M \(HCl\)
- titrating a solution of trimethylamine (\(Me_3N\)) with 0.150 M \(HNO_3\)
- titrating a solution of aniline hydrochloride (\(C_6H_5NH_3^+Cl^−\)) with 0.050 M \(KOH\)
4. For the titration of any strong acid with any strong base, the \(pH\) at the equivalence point is 7.0. Why is this not usually the case in titrations of weak acids or weak bases?
5. Why are the titration curves for a strong acid with a strong base and a weak acid with a strong base identical in shape above the equivalence points but not below?
6. Describe what is occurring on a molecular level during the titration of a weak acid, such as acetic acid, with a strong base, such as \(NaOH\), at the following points along the titration curve. Which of these points corresponds to \(pH=pK_{a}\)?
- at the beginning of the titration
- at the midpoint of the titration
- at the equivalence point
- when excess titrant has been added
7. On a molecular level, describe what is happening during the titration of a weak base, such as ammonia, with a strong acid, such as \(HCl\), at the following points along the titration curve. Which of these points corresponds to \(pOH=pK_{b}\)?
- at the beginning of the titration
- at the midpoint of the titration
- at the equivalence point
- when excess titrant has been added
8. For the titration of a weak acid with a strong base, use the \(K_{a}\) expression to show that \(pH=pK_{a}\) at the midpoint of the titration.
9. Chemical indicators can be used to monitor \(pH\) rapidly and inexpensively. Nevertheless, electronic methods are generally preferred. Why?
10. Why does adding ammonium chloride to a solution of ammonia in water decrease the pH of the solution?
11. Given the equilibrium system \(CH_3CO_2H\,(aq) \rightleftharpoons CH_3CO_2^{-}\,(aq) + H^{+}\,(aq)\), explain what happens to the position of the equilibrium and the \(pH\) in each case.
- Dilute \(HCl\) is added.
- Dilute \(NaOH\) is added.
- Solid sodium acetate is added.
12. Given the equilibrium system \(CH_3NH_2\,(aq) + H_2O\,(l) \rightleftharpoons CH_{3}NH_3^{+}\,(aq) + OH^{-}\,(aq)\), explain what happens to the position of the equilibrium and the \(pH\) in each case.
- Dilute \(HCl\) is added.
- Dilute \(NaOH\) is added.
- Solid \(CH_3NH_3^{+}Cl^{−}\) is added.
Answers
1. The portion of the titration curve that lies below the equivalence point of a solution of a weak acid is displaced upward relative to the titration curve of a strong acid because the starting point of a weak acid is at a higher \(pH\) compared to that of a strong acid. The slope for a strong acid is greater compared to that of a weak acid because when a weak acid is neutralized, the solution that remains is basic because the acid’s conjugate base remains in solution.
2.
a. The solution will be neutral at the equivalence point because sodium hydroxide is a strong base and hydrochloric acid is a strong acid.
b. The solution will be acidic at the equivalence point because ethylamine is a weak base and nitric acid is a strong acid.
c. The solution will be basic at the equivalence point because aniline hydrochloride is a weak acid and potassium hydroxide is a strong base.
3.
a. Barium hydroxide is a strong base and hydrochloric acid is a strong acid thus phenol red with the \(pK_a=7.4\) is best suited for the reaction.
b. Trimethylamine is a weak base and nitric acid is a strong acid thus bromophenol blue with the \(pK_a=4.1\) is best suited for the reaction.
c. Aniline hydrochloride is a weak acid and potassium hydroxide is a strong base thus phenolphthalein with \(pK_a=9.5\) is best suited for the reaction.
4. This is not usually the case in the titration of weak acids and weak bases because weak acids and weak bases would only ionize partially, thus complete neutralization does not occur.
5. The titration curve for a strong acid with a strong base is identical in shape above the equivalence point of the titration curve with a weak acid and strong base because both cases involve the addition of strong base. Not only does the strong base completely neutralize the acid but there is an excess of a strong base that makes the solution basic.
6.
a. The titration begins with a \(pH\) is higher than the titration of a strong acid. At the beginning of the titration, there is a sharp increase in \(pH\) because the anion of the weak acid becomes a common ion that reduces the ionization of the acid.
b. There is a sharp increase at the beginning of the titration that changes gradually due to the solution becoming a buffer. This continues until the strong base has overcome the buffer capacity. At the midpoint of the titration, the concentration of the weak acid is equal to the concentration of its conjugate base. This point is also known as half-neutralization because half the acid has been neutralized by the strong base.
c. At the equivalence point the pH is greater than 7 because the acid (\(HA\)) has been converted to its conjugate base (\(A^{-}\)) by sodium hydroxide and equilibrium moves backward toward the acid and produces hydroxide:
\(A^{-}+H_2O \rightleftharpoons AH+OH^{-}\)
d. When the excess titrant has been added the solution becomes basic because sodium hydroxide completely neutralized the weak acid.
7.
a. The titration begins with a \(pH\) that is lower than the titration of a strong base but higher than the \(pH=7\). At the beginning of the titration, there is a sharp decrease in \(pH\) because the cation of the weak base becomes a common ion that reduces the ionization of the base.
b. The sharp decrease at the beginning of the titration changes gradually due to the solution becoming a buffer. This continues until the strong acid has overcome the buffer capacity. At the midpoint of the titration, the concentration of the weak base is equal to the concentration of its conjugate acid \(pH=pK_a\). This point is also known as half-neutralization because half the base has been neutralized by the strong acid.
c. At the equivalence point the \(pH\) is less than 7 because the base \(NH_{3}\) has been converted to its conjugate acid \(NH_{4}^{+}\) by hydrochloric acid and equilibrium moves forwards toward the base and produces \(NH_{4}Cl^{-}\):
\(NH_{3}+HCl \rightleftharpoons NH_{4}Cl\)
d. When excess titrant has been added the solution becomes acidic because hydrochloric acid completely neutralized the weak base.
8.
\(HA \overset{K_a}{\rightleftharpoons} A^{-}+H^{+}\)
\(K_a= \frac{[H^{+}][A^{-}]}{[HA]}\)
\(pH=pK_a+log(\frac{[A^{-}]}{[HA]}\)
Assume \([A^{-}]=[HA]=1\)
\(pH=pK_a+log(1)\)
\(pH=pK_a+0\)
\(pH=pK_a\)
9. Electronic methods are preferred over chemical indicators because it is a more accurate method at determining the pH. Also, chemical indicators must be selected to observe a narrow pH range while electronic methods observe a wider range.
10.
Ammonia is a weak base and dissociates in water as:
\(NH_3\,(aq)+H_2O\,(l) \rightleftharpoons NH_4^{+}\,(aq)+OH^{-}\,(aq)\)
When \(NH_4Cl\) is added, it 100% dissociates into \(NH_4^{+}\) and \(Cl^{-}\) in water:
\(NH_{4}Cl\,(aq) \rightleftharpoons NH_{4}^{+}\,(aq)+Cl^{-}\,(aq)\)
Due to common ion, \(NH_4^{+}\,(aq)\) the dissociation of \(NH_{3}\) will decrease. Thus, the concentration of \(OH^{-}\,(aq)\) decreases and the concentration of \(H_{3}O^{+}\) increases.
Since \(pH=-log(H_{3}O^{+})\) the \(pH\) and \(H_{3}O^{+}\) are inversely related, the concentration of \(H_{3}O^{+}\) concentration increases and \(pH\) decreases.
11.
a. The position of equilibrium shift to the left and the pH decreases.
b. The position of equilibrium shifts to the right and the pH increases.
c. The position of equilibrium shifts to the left and the pH increases.
12.
a. The position of equilibrium shifts to the left and the pH decreases.
b. The position of equilibrium shifts to the left and the pH increases.
c. The position of equilibrium shifts to the left and the pH increases.
Numerical Problems
1. Calculate the pH of each solution.
- A volume of 25.0 mL of 6.09 M HCl is added to 100.0 mL of distilled water
- A volume of 5.0 mL of 2.55 M \(NaOH\) is added to 75.0 mL of distilled water.
2. What is the pH of a solution prepared by mixing 50.0 mL of 0.225 M HCl with 100.0 mL of a 0.184 M solution of \(NaOH\)?
3. What volume of 0.50 M HCl is needed to completely neutralize 25.00 mL of 0.86 M \(NaOH\)?
4.Calculate the final pH when each pair of solutions is mixed.
- 100 mL of 0.105 M HCl and 100 mL of 0.115 M sodium acetate
- 50 mL of 0.10 M HCl and 100 mL of 0.15 M sodium acetate
- 100 mL of 0.109 M acetic acid and 100 mL of 0.118 M \(NaOH\)
- 100 mL of 0.998 M acetic acid and 50.0 mL of 0.110 M \(NaOH\)
5. Calculate the final pH when each pair of solutions is mixed.
- 100 mL of 0.983 M HCl and 100 mL of 0.102 M sodium fluoride
- 50.0 mL of 0.115 M HCl and 100 mL of 0.109 M sodium fluoride
- 100 mL of 0.106 M hydrofluoric acid and 50.0 mL of 0.996 M \(NaOH\)
- 100 mL of 0.107 M sodium acetate and 50.0 mL of 0.987 M acetic acid
6. Calcium carbonate is a major contributor to the “hardness” of water. The amount of CaCO3 in a water sample can be determined by titrating the sample with an acid, such as HCl, which produces water and CO2. Write a balanced chemical equation for this reaction. Generate a plot of solution pH versus volume of 0.100 M HCl added for the titration of a solution of 250 mg of CaCO3 in 200.0 mL of water with 0.100 M HCl; assume that the HCl solution is added in 5.00 mL increments. What volume of HCl corresponds to the equivalence point?
7. For a titration of 50.0 mL of 0.288 M \(NaOH\), you would like to prepare a 0.200 M HCl solution. The only HCl solution available to you, however, is 12.0 M.
- How would you prepare 500 mL of a 0.200 M HCl solution?
- Approximately what volume of your 0.200 M HCl solution is needed to neutralize the \(NaOH\) solution?
- After completing the titration, you find that your “0.200 M” HCl solution is actually 0.187 M. What was the exact volume of titrant used in the neutralization?
8. While titrating 50.0 mL of a 0.582 M solution of HCl with a solution labeled “0.500 M KOH,” you overshoot the endpoint. To correct the problem, you add 10.00 mL of the HCl solution to your flask and then carefully continue the titration. The total volume of titrant needed for neutralization is 71.9 mL.
- What is the actual molarity of your KOH solution?
- What volume of titrant was needed to neutralize 50.0 mL of the acid?
9. Complete the following table and generate a titration curve showing the pH versus volume of added base for the titration of 50.0 mL of 0.288 M HCl with 0.321 M \(NaOH\). Clearly indicate the equivalence point.
| Base Added (mL) | 10.0 | 30.0 | 40.0 | 45.0 | 50.0 | 55.0 | 65.0 | 75.0 |
| pH |
10. The following data were obtained while titrating 25.0 mL of 0.156 M \(NaOH\) with a solution labeled “0.202 M HCl.” Plot the pH versus volume of titrant added. Then determine the equivalence point from your graph and calculate the exact concentration of your HCl solution.
| Volume of HCl (mL) | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| pH | 11.46 | 11.29 | 10.98 | 4.40 | 2.99 | 2.70 | 2.52 |
11. Fill in the data for the titration of 50.0 mL of 0.241 M formic acid with 0.0982 M KOH. The pKa of formic acid is 3.75. What is the pH of the solution at the equivalence point?
| Volume of Base Added (mL) | 0 | 5 | 10 | 15 | 20 | 25 |
| pH |
12. Glycine hydrochloride, which contains the fully protonated form of the amino acid glycine, has the following structure:
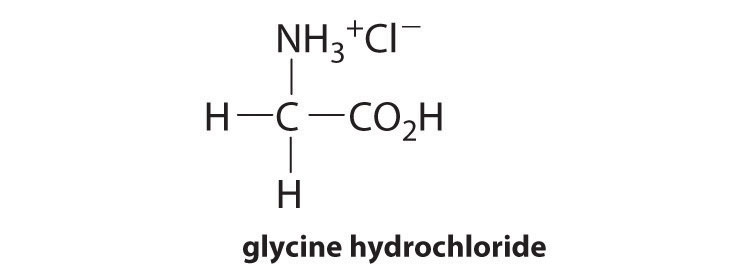
It is a strong electrolyte that completely dissociates in water. Titration with base gives two equivalence points: the first corresponds to the deprotonation of the carboxylic acid group and the second to loss of the proton from the ammonium group. The corresponding equilibrium equations are as follows:
\[ ^{+}NH_{3}-CH_{2}-CO_{2}H\left ( aq \right ) \rightleftharpoons \;\;\;\;\; pK_{a1}=2.3\]
\[ ^{+}NH_{3}-CH_{2}-CO_{2}\left ( aq \right )+ H^{+} \]
\[ ^{+}NH_{3}-CH_{2}-CO_{2}\left ( aq \right ) \rightleftharpoons \;\;\;\;\; pK_{a2}=9.6\]
\[ NH_{2}-CH_{2}-COO\left ( aq \right )+ H^{+} \]
Given 50.0 mL of solution that is 0.430 M glycine hydrochloride, how many milliliters of 0.150 M KOH are needed to fully deprotonate the carboxylic acid group?
- How many additional milliliters of KOH are needed to deprotonate the ammonium group?
- What is the pH of the solution at each equivalence point?
- How many milliliters of titrant are needed to obtain a solution in which glycine has no net electrical charge? The pH at which a molecule such as glycine has no net charge is its isoelectric point. What is the isoelectric point of glycine?
13. What is the pH of a solution prepared by adding 38.2 mL of 0.197 M HCl to 150.0 mL of 0.242 M pyridine? The pKb of pyridine is 8.77.
14. What is the pH of a solution prepared by adding 40.3 mL of 0.289 M \(NaOH\) to 150.0 mL of 0.564 M succinic acid (\(HO_2CCH_2CH_2CO_2H\))? (For succinic acid, pKa1 = 4.21 and pKa2 = 5.64).
14. Calculate the pH of a 0.15 M solution of malonic acid (\(HO_2CCH_2CO_2H\)), whose pKa values are as follows: pKa1 = 2.85 and pKa2 = 5.70.
Answers
1.
a.\(pH=-log([H_3O^{+}])=-log(1.218)=-0.086\)
\([HCl]=[H^{+}]\)
\(M_{1}V_{1}=M_{2}V_{2} \rightarrow (6.09\,M)(25\,mL)=(x)(125\,mL) \rightarrow x=1.218\)
b. \(pH+pOH=14 \rightarrow pH=14-pOH=14-0.80=13\)
\(pOH=-log([OH^{-}])=-log(0.159)=0.80\)
\([NaOH]=[OH^{-}]\)
\(M_{1}V_{1}=M_{2}V_{2} \rightarrow (2.55\,M)(5.0\,mL)=(x)(80\,mL) \rightarrow x=0.159\)
2.
\(pH+pOH=14 \rightarrow pH=14-pOH=14-1.321=12.7\)
\(HCl:50.0\,mL \times \frac{1\,L}{1,000\,mL} \times \frac{0.225\,mol}{1\,L}=0.01125\,mol\)
\(NaOH:100.0\,mL \times \frac{1\,L}{1,000\,mL} \times \frac{0.184\,mol}{1\,L}=0.0184\,mol\)
Note the number of moles for \(NaOH\) is greater than \(HCl\), therefore we calculate \(pOH\).
\(0.0184-0.01125=0.00715\,mol\)
\(\frac{0.00715\,mol}{.15\,L}=0.0477\)
\(pOH=-log([OH^{-}])=-log(0.0477)=1.321\)
3. \(M_{1}V_{1}=M_{2}V_{2} \rightarrow (0.50\,M)(x\,L)=(0.86\,M)(0.25\,L) \rightarrow x\,L=4.3 \times 10^{-2}\,L\)
4. Video Solution
a. \(pH=pK_a+log(\frac{C_{2}H_{3}NaO_{2}}{C_{2}H_{4}O_{2}})=4.76+log(\frac{0.0935}{0.0105})=5.71\)
\(HCl: 100\,mL \times \frac{1\,L}{1,000\,mL} \times \frac{0.0105\,mol}{1\,L}=0.0105\,mol\)
\(C_2H_3NaO_2: 100\,mL \times \frac{1\,L}{1,000\,mL} \times \frac{0.115\,mol}{1\,L}=0.0115\,mol\)
\(C_{2}H_{3}NaO_{2}\,(s)+HCl\,(aq) \rightarrow C_{2}H_{4}O_{2}\,(aq)+NaCl\,(s)\)
|
\(C_{2}H_{3}NaO_{2}\) |
\(HCl\) |
\(C_{2}H_{4}O_{2}\) |
\(NaCl\) |
|
|
I |
0.0115 |
0.0105 |
0 |
- |
|
C |
-0.0105 |
-0.0105 |
+0.0105 |
- |
|
E |
0.0935 |
0 |
0.0105 |
- |
b. \(pH=pK_a+log(\frac{C_{2}H_{3}NaO_{2}}{C_{2}H_{4}O_{2}})=4.76+log(\frac{0.01}{0.005})=5.05\)
\(HCl: 100\,mL \times \frac{1\,L}{1,000\,mL} \times \frac{0.0105\,mol}{1\,L}=0.005\,mol\)
\(C_2H_3NaO_2: 100\,mL \times \frac{1\,L}{1,000\,mL} \times \frac{0.115\,mol}{1\,L}=0.015\,mol\)
\(C_{2}H_{3}NaO_{2}\,(s)+HCl\,(aq) \rightarrow C_{2}H_{4}O_{2}\,(aq)+NaCl\,(s)\)
|
\(C_{2}H_{3}NaO_{2}\) |
\(HCl\) |
\(C_{2}H_{4}O_{2}\) |
\(NaCl\) |
|
|
I |
0.015 |
0.005 |
0 |
0 |
|
C |
-0.005 |
-0.005 |
+0.005 |
+0.005 |
|
E |
0.01 |
0 |
0.005 |
0.005 |
c. \(pH=14-pOH=14-(-log(\frac{0.0118-0.0109}{0.2\,L}))=11.7\)
\(CH_{3}COOH: 0.1\,L \times 0.109\,M=0.0109\,mol\)
\(NaOH: 0.1\,L \times 0.118\,M=0.0118\,mol\)
\(CH_{3}COOH\,(aq)+NaOH\,(aq) \rightarrow H_{2}O\,(l)+CH_{3}COO^{-}Na\,(aq)\)
|
\(CH_{3}COOH\) |
\(NaOH\) |
\(H_{2}O\) |
\(CH_{3}COONa\) |
|
|
I |
0.0109 |
0.0118 |
- |
0 |
|
C |
-0.0109 |
-0.0109 |
- |
+0.0109 |
|
E |
0 |
\(9 \times 10^{-4}\) |
- |
0.0109 |
d. \(pH=4.76+log(\frac{0.0055}{0.0943})=3.53\)
\(CH_{3}COOH:0.1\,L \times 0.998\,M=0.0998\,mol\)
\(NaOH: 0.05\,L \times 0.110\,M=0.0055\,mol\)
\(CH_{3}COOH\,(aq)+NaOH\,(aq) \rightarrow H_{2}O\,(l)+CH_{3}COONa\,(aq)\)
|
\(CH_{3}COOH\) |
\(NaOH\) |
\(H_{2}O\) |
\(CH_{3}COONa\) |
|
|
I |
0.0998 |
0.0055 |
- |
0 |
|
C |
-0.0055 |
-0.0055 |
- |
+0.0055 |
|
E |
0.0943 |
0 |
- |
0.0055 |
5. Video Solution
a. \(pH=-log(\frac{0.9728}{0.2\,L})=4.86\)
\(HCl:100\,mL \times \frac{1\,L}{1,000\,L} \times0.983\,M=0.983\,mol\)
\(NaF:100\,mL \times \frac{1\,L}{1,000\,L} \times 0.102\,M=0.0102\,mol\)
\(HCl\,(aq)+NaF\,(s) \rightarrow NaCl\,(aq)+HF\,(aq)\)
|
\(HCl\) |
\(NaF\) |
\(NaCl\) |
\(HF\) |
|
|
I |
0.983 |
0.0102 |
- |
0 |
|
C |
-0.0102 |
-0.0102 |
- |
-0.0102 |
|
E |
0.9728 |
0 |
- |
-0.0102 |
b. \(pH=pK_a+log(\frac{[NaF]}{[HF]})=3.14+log(\frac{0.00515}{0.00575})=3.09\)
\(HCl:50\,mL \times \frac{1\,L}{1,000\,L} \times 0.115\,M=0.00575\,mol\)
\(NaF:100\,mL \times \frac{1\,L}{1,000\,L} \times 0.109\,M=0.0109\,mol\)
\(HCl\,(aq)+NaF\,(s) \rightarrow NaCl\,(aq)+HF\,(aq)\)
|
\(HCl\) |
\(NaF\) |
\(NaCl\) |
\(HF\) |
|
|
I |
0.00575 |
0.0109 |
- |
0 |
|
C |
-0.00575 |
-0.00575 |
- |
+0.00575 |
|
E |
0 |
0.00515 |
- |
0.00575 |
c. \(pH=14-pOH=14-(-log(0.0498-0.0106))=12.6\)
\(HF:100\,mL \times \frac{1\,L}{1,000\,L} \times 0.106\,M=0.0106\,mol\)
\(NaOH: 50\,mL \times \frac{1\,L}{1,000\,L} \times 0.996\,M=0.0498\,mol\)
\(HF\,(aq)+NaOH\,(aq) \rightarrow NaF\,(aq)+H_{2}O\,(aq)\)
\(HCl(aq)+NaOH(aq) \rightarrow NaCl\,(aq)+H_2O\)
d.\(pH=pK_a+log(\frac{[C_2H_3NaO_2]}{[CH_{3}COOH]})=4.76+log(\frac{0.0107}{0.04935})=4.10\)
\(C_2H_3NaO_2: 0.1\,L \times 0.107\,M=0.0107\)
\(CH_3COOH: 0.05\,mL \times 0.987\,M=0.04935\)
\(CH_{3}COOH\,(aq)+H_{2}O \rightarrow C_2H_3O^{-}+H_3O^{+}\)
6.
\(CaCO_{3}\,(aq)+2\,HCl\,(aq) \rightarrow CaCl_{2}\,(aq)+H_2O\,(l)+CO_{2}\,(g)\)
\(CO_{3}^{2-}\,(aq)+H^{+}\,(aq) \rightleftharpoons HCO_{3}^{-}\,(aq)\)
\(HCO_{3}^{2-}\,(aq)+H^{+}\,(aq) \rightleftharpoons H_{2}CO_{3}\,(aq)\)
\(K_{a1}=4.3 \times 10^{-7}\)
\(K_{a2}=5.0 \times 10^{-11}\)
At 0 mL addition of \(HCl\): \(pH=14-pOH=14-(-log(\sqrt{0.0125 \times \frac{10^{-14}}{5.0 \times 10^{-11}}})=11.20\)
\(CaCO_{3}:250\,mg \times \frac{1\,g}{1,000\,mg} \times \frac{1\,mol}{100.0869\,g} \times \frac{1}{200\,mL \times \frac{1\,L}{1,000\,mL}}=0.0125\,M\)
At 5 mL addition of \(HCl\): \(pH=-log(5 \times 10^{-11})+log(\frac{0.002}{0.0005})=10.9\)
\(CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.005\,L \times 0.1\,M=0.0005\,mol\)
|
\(CO_{3}^{2-}\) |
\(H^{+}\) |
\(HCO_{3}^{-}\) |
|
|
I |
0.0025 |
0.0005 |
0 |
|
C |
-0.0005 |
-0.0005 |
0.0005 |
|
E |
0.002 |
0 |
0.0005 |
At 10 mL addition of \(HCl\): \(pH=-log(5 \times 10^{-11})+log(\frac{0.001}{0.0015})=10.5\)
\(CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.01\,L \times 0.1\,M=0.001\,mol\)
|
\(CO_{3}^{2-}\) |
\(H^{+}\) |
\(HCO_{3}^{-}\) |
|
|
I |
0.0025 |
0.001 |
0 |
|
C |
-0.001 |
-0.001 |
0.001 |
|
E |
0.0015 |
0 |
0.001 |
At 15 mL addition of \(HCl\):\(pH=-log(5 \times 10^{-11})+log(\frac{0.001}{0.0015})=10.1\)
\(CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.015\,L \times 0.1\,M=0.0015\,mol\)
|
\(CO_{3}^{2-}\) |
\(H^{+}\) |
\(HCO_{3}^{-}\) |
|
|
I |
0.0025 |
0.0015 |
0 |
|
C |
-0.0015 |
-0.0015 |
0.0015 |
|
E |
0.001 |
0 |
0.0015 |
At 20 mL addition of \(HCl\):\(pH=-log(5 \times 10^{-11})+log(\frac{5 \times 10^{-4}}{0.002})=9.7\)
\(CaCO_{3}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.02\,L \times 0.1\,M=0.002\,mol\)
|
\(CO_{3}^{2-}\) |
\(H^{+}\) |
\(HCO_{3}^{-}\) |
|
|
I |
0.0025 |
0.002 |
0 |
|
C |
-0.002 |
-0.002 |
0.002 |
|
E |
\(5 \times 10^{-4}\) |
0 |
0.002 |
At 25 mL addition of \(HCl\): first equivalence point: \(pH=\frac{-log(K_{a1})-log(K_{a2})}{2}=\frac{-log(4.3 \times 10^{-7})-log(5.0 \times 10^{-11})}{2}=8.33\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.025\,L \times 0.1\,M=0.0025\,mol\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.0025 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0 |
0.0025 |
At 30 mL addition of \(HCl\): \(pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.0005})=7.07\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.03\,L \times 0.1\,M=0.003\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.003 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
\(5 \times 10^{-4}\) |
0.0025 |
At 35 mL addition of \(HCl\): \(pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.001})=6.76\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.035\,L \times 0.1\,M=0.0035\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.0035 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.001 |
0.0025 |
At 40 mL addition of \(HCl\): \(pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.003})=6.59\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.040\,L \times 0.1\,M=0.004\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.004 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.0015 |
0.0025 |
At 45 mL addition of \(HCl\): \(pH=-log(4.3 \times 10^{-7})+log(\frac{0.0025}{0.002})=6.46\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.045\,L \times 0.1\,M=0.0045\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.0045 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.002 |
0.0025 |
At 50 mL addition of \(HCl\): second equivalence point: \(pH=3.86\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.05\,L \times 0.1\,M=0.005\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.005 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.0025 |
0.0025 |
At 55 mL addition of \(HCl\): \(pH=-log(\frac{0.003}{0.055})=1.26\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.055\,L \times 0.1\,M=0.0055\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.0055 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.003 |
0.0025 |
At 60 mL addition of \(HCl\): \(pH=-log(\frac{0.0035}{0.06})=1.23\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.06\,L \times 0.1\,M=0.006\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.006 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.0035 |
0.0025 |
At 65 mL addition of \(HCl\): \(pH=-log(\frac{0.0040}{0.065})=1.21\)
\(HCO_{3}^{-}:0.2\,L \times 0.0125\,M=0.0025\,mol\)
\(HCl: 0.06\,L \times 0.1\,M=0.006\)
|
\(HCO_{3}^{-}\) |
\(H^{+}\) |
\(H_{2}CO_{3}\) |
|
|
I |
0.0025 |
0.0065 |
0 |
|
C |
-0.0025 |
-0.0025 |
0.0025 |
|
E |
0 |
0.0040 |
0.0025 |
7. Video Solution
-
\(M_1V_1=M_2V_2 \rightarrow V_2=\frac{M_1V_1}{V_2}=\frac{(0.2\,M)(0.5\,L)}{12.0\,M}=8.33 \times10^{-3}\,L\) Therefore, dilute 8.33 mL of 12.0 M HCl to 500.0 mL.
-
\(M_1V_1=M_2V_2 \rightarrow V_2=\frac{M_1V_1}{V_2}=\frac{(0.288\,M)(0.05\,L)}{0.2\,M}=7.20 \times 10^{-3}\,L\)
-
\(M_1V_1=M_2V_2 \rightarrow V_2=\frac{M_1V_1}{V_2}=\frac{(0.288\,M)(0.05\,L)}{0.187\,M}=7.70 \times 10^{-2}\)
8.
a. \(M_{1}V_{1}=M_{2}V_{2} \rightarrow M_2= \frac{M_1V_1}{V_{2}}=\frac{(0.582\,M)(0.060\,L)}{0.0719\,L} =0.49\,M\)
b. \(M_{1}V_{1}=M_{2}V_{2} \rightarrow V_{2}=\frac{M_{1}V_{1}}{M_{2}} =\frac{(0.582\,M)(0.050\,L)}{0.49\,M}=59.4 \times 10^{-2}\,L\)
9.
| Volume of Base Added (mL) | 10.0 | 30.0 | 40.0 | 45.0 | 50.0 | 55.0 | 65.0 | 75.0 |
| pH | 0.73 | 1.22 | 1.76 | 7 | 12.2 | 12.5 | 13.0 | 13.1 |
\(NaOH\,(aq)+HCl\,(aq) \rightarrow NaCl\,(s)+H_{2}O\,(l)\)
At 0 mL of base added: \(pH=-log(0.288)=0.54\)
At 10 mL of base added: \(pH=-log(\frac{0.0144-0.00321}{0.06})=0.73\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.01\,L \times 0.321\,M=0.00321\)
At 30 mL of base added: \(pH=-log(\frac{0.0144-0.00963}{0.08})=1.22\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.03\,L \times 0.321\,M=0.00963\)
At 40.0 mL of base added: \(pH=-log(\frac{0.0144-0.01284}{0.09})=1.76\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.04\,L \times 0.321\,M=0.01284\)
At 45.0 mL of base added: \(pH=7\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.045\,L \times 0.321\,M=0.0144\)
All \(HCl\) will neutralize at the equivalence point \([H^{+}]=[OH^{-}]\) and the pH of the solution is 7.
At 50.0 mL base added: \(pH=14-pOH=14-log(\frac{0.01605-0.0144}{0.1})=12.2\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.050\,L \times 0.321\,M=0.01605\)
At 55 mL base added: \(pH=14-pOH=14-log(\frac{0.01605-0.0144}{0.1})=12.5\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.055\,L \times 0.321\,M=0.017655\)
At 65 mL base added: \(pH=14-pOH=14-log(\frac{0.020865-0.0144}{0.07})=13.0\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.065\,L \times 0.321\,M=0.020865\)
At 75 mL base added: \(pH=14-pOH=14-log(\frac{0.024075-0.0144}{0.08})=13.1\)
\(HCl:0.05\,L \times 0.288\,M=0.0144\)
\(NaOH:0.075\,L \times 0.321\,M=0.024075\)
10.
The equivalence point is at \(pH\) 7 and this occurs at 0.0193 L.
\(V_{2}=\frac{(0.156\,M)(0.025\,L)}{0.202}=0.0193\,L\)
11.
pH at equivalence point: \(14-(-log\sqrt{(\frac{10^{-14}}{10^{-3.75}} \times \frac{0.01205}{0.05+0.1227}}))=8.30\)
\(0.05\,L \times 0.241\,M=0.01205\,mol\)
\(V_2=\frac{(0.05\,L)(0.241\,M)}{0.0982}=0.1227\,L\)
| Volume of Base Added (mL) | 0 | 5 | 10 | 15 | 20 | 25 |
| pH | 2.18 | 2.38 | 2.70 | 2.89 | 3.04 | 3.16 |
At 0 mL of base added: \(pH=-log([H^{+}])=-log(2.52 \times 10^{-6})=2.18\)
\([H^{+}]= \sqrt{10^{-3.75} \times 0.241\,M}=2.52 \times 10^{-6}\)
At 5 mL of base added: \(pH=3.75+log(\frac{4.91 \times 10^{-4}}{0.01205-4.91 \times 10^{-4}})=2.38\)
\(KOH:0.05\,L \times 0.0982\,M=4.91 \times 10^{-4}\,mol\)
\(CH_{2}O_{2}: 0.05\,L \times 0.241\,M=0.01205\,mol\)
At 10 mL of base added: \(pH=3.75+log(\frac{9.82 \times 10^{-4}}{0.01205-9.82 \times 10^{-4}})=2.70\)
\(KOH:0.01\,L \times 0.0982\,M=9.82 \times 10^{-4}\,mol\)
\(CH_{2}O_{2}: 0.05\,L \times 0.241\,M=0.01205\,mol\)
At 15 mL of base added:\(pH=3.75+log(\frac{0.001473}{0.01205-0.001473}=2.89\)
\(KOH: 0.015\,L \times 0.0982\,M=0.001473\)
\(CH_{2}O_{2}: 0.05\,L \times 0.241\,M=0.01205\)
At 20 mL of base added: \(pH=3.75+log(\frac{0.001964}{0.01205-0.001964})=3.04\)
\(KOH: 0.02\,L \times 0.0982\,M=0.001964\)
\(CH_{2}O_{2}: 0.05\,L \times 0.241\,M=0.01205\)
At 25 mL base added: \(pH=3.75+log(\frac{0.002455}{0.01205-0.002455})=3.16\)
\(KOH:0.025\,L \times 0.0982\,M=0.002455\,mol\)
\(CH_{2}O_{2}: 0.05\,L \times 0.241\,M=0.01205\)
12. \(M_1V_1=M_2V_2 \rightarrow V_2=\frac{M_1V1}{M_2}=\frac{(0.430\,M)(0.05\,L)}{0.150\,M}=1.42 \times 10^{-1}\,L\)
143 mL are needed to fully deprotonate the carboxylic acid group.
a. 143 additional milliliters of KOH are needed to deprotonate the ammonium group.
b. At the first equivalence point: \(pH=\frac{(pKa_{1}+pKa_{2})}{2}=5.95\)
c. 143 mL of titrant are needed to obtain a solution in which glycine has no electrical charge. The isoelectric point of glycine 5.95.
13.
\(pH=pK_a+log(\frac{[C_5H_5N]}{[C_5H_5NH^{+}]})=(14-8.77)+log(\frac{0.02996}{0.0063434})=5.90\)
\(C_5H_5N\,(aq)+HCl\,(aq) \rightarrow C_5H_5NH^{+}\,(aq)+Cl^{-}\,(aq)\)
\(HCl: 32.2\,mL \times \frac{1\,L}{1,000\,mL} \times 0.197\,M=0.0063434\,mol\)
\(C_5H_5N: 150\,mL \times \frac{1\,L}{1,000\,mL} \times 0.242\,M=0.0363\,mol\)
|
\(C_5H_5N\) |
\(HCl\) |
\(C_5H_5NH^{+}\) |
\(Cl^{-}\) |
|
|
I |
0.0363 |
0.0063434 |
0 |
- |
|
C |
-0.0063434 |
-0.0063434 |
+0.0063434 |
- |
|
E |
0.02996 |
0 |
0.0063434 |
- |
14. \(pH=\frac{(4.21+5.64)}{2}=4.93\)
15. \(pH=\frac{(2.85+5.70)}{2}=4.25\)
17.4: Solubility Equilibria
Conceptual Problems
- Write an expression for Ksp for each salt.
- \(AgI\)
- \(CaF_{2}\)
- \(PbCl_2\)
- \(Ag_{2}CrO_{4}\)
- Some species are not represented in a solubility product expression. Why?
- Describe the differences between \(Q\) and \(K_{sp}\).
- How can an ion product be used to determine whether a solution is saturated?
- When using Ksp to directly compare the solubilities of compounds, why is it important to compare only the Ksp values of salts that have the same stoichiometry?
- Describe the effect of a common ion on the solubility of a salt. Is this effect similar to the common ion effect found in buffers? Explain your answer.
- Explain why the presence of MgCl2 decreases the molar solubility of the sparingly soluble salt MgCO3.
Conceptual Answers
a. \(K_{sp}=[Ag^{+}][I^{-}]\)
b. \(K_{sp}=[Ca^{2+}][F^{-}]^{2}\)
c. \(K_{sp}=[Pb^{2+}][Cl^{-}]^{2}\)
d. \(K_{sp}=[Ag^{+}]^{2}[CrO_{4}^{2-}]\)
2. The solubility constant expression, \(K_{sp}\) is an equilibrium constant for a solid substance dissolving in a an aqueous solution. Thus, it is a measure of solubility and species that do not dissolve are not represented in the solubility product expression.
3. The main difference between \(Q\) and \(K_sp\) is that \(Q\) describes a reaction that is not at equilibrium unlike \(K_{sp}\).
4. An ion product can be used to determine whether a solution is saturated as it is compared to \(K_{sp}\) where there are three possible conditions for an aqueous solution of an ionic solid:
-
\(Q<K_{sp}\). The solution is unsaturated, and more of the ionic solid, if available, will dissolve.
-
\(Q=K_{sp}\). The solution is saturated and at equilibrium.
-
\(Q>K_{sp}\). The solution is supersaturated, and ionic solid will precipitate.
- For a 1:1 salt, the molar solubility is simply \(\sqrt{K_{\textrm{sp}}}\); for a 2:1 salt, the molar solubility is \(\sqrt[3]{K_{\textrm{sp}}/4}\). Consequently, the magnitudes of Ksp can be correlated with molar solubility only if the salts have the same stoichiometry.
- By the presence of a common ion, the solubility of any sparingly soluble salt is always decreased. This is similar to the common ion effect found in buffers as adding a common cation or anion shifts the solubility equilibrium in the direction predicted by Le Chatelier’s principle.
- Because of the common ion effect. Adding a soluble Mg2+ salt increases [Mg2+] in solution, and Le Chatelier’s principle predicts that this will shift the solubility equilibrium of MgCO3 to the left, decreasing its solubility.
Numerical Problems
- Predict the molar solubility of each compound using the Ksp values given in Chapter 26.
- \(Cd(IO_{3})_{2}\)
- \(AgCN\)
- \(HgI_{2}\)
- Predict the molar solubility of each compound using the Ksp values given.
- Li3PO4: 2.37 × 10−11
- Ca(IO3)2: 6.47 × 10−6
- Y(IO3)3: 1.12 × 10−10
- A student prepared 750 mL of a saturated solution of silver sulfate (Ag2SO4). How many grams of Ag2SO4 does the solution contain? Ksp = 1.20 × 10−5.
- Given the Ksp values in Table 17.1 "Solubility Products for Selected Ionic Substances at 25°C" and Appendix B, predict the molar concentration of each species in a saturated aqueous solution.
- silver bromide
- lead oxalate
- iron(II) carbonate
- silver phosphate
- copper(I) cyanide
- Given the Ksp values in Table 17.1 "Solubility Products for Selected Ionic Substances at 25°C" and Appendix B predict the molar concentration of each species in a saturated aqueous solution.
- copper(I) chloride
- lanthanum(III) iodate
- magnesium phosphate
- silver chromate
- strontium sulfate
- Silicon dioxide, the most common binary compound of silicon and oxygen, constitutes approximately 60% of Earth’s crust. Under certain conditions, this compound can react with water to form silicic acid, which can be written as either H4SiO4 or Si(OH)4. Write a balanced chemical equation for the dissolution of SiO2 in basic solution. Write an equilibrium constant expression for the reaction.
- The Kspof Mg(OH)2 is 5.61 × 10−12. If you tried to dissolve 24.0 mg of Mg(OH)2 in 250 mL of water and then filtered the solution and dried the remaining solid, what would you predict to be the mass of the undissolved solid? You discover that only 1.0 mg remains undissolved. Explain the difference between your expected value and the actual value.
- The Ksp of lithium carbonate is 8.15 × 10−4. If 2.34 g of the salt is stirred with 500 mL of water and any undissolved solid is filtered from the solution and dried, what do you predict to be the mass of the solid? You discover that all of your sample dissolves. Explain the difference between your predicted value and the actual value.
- You have calculated that 24.6 mg of BaSO4 will dissolve in 1.0 L of water at 25°C. After adding your calculated amount to 1.0 L of water and stirring for several hours, you notice that the solution contains undissolved solid. After carefully filtering the solution and drying the solid, you find that 22.1 mg did not dissolve. According to your measurements, what is the Ksp of barium sulfate?
- In a saturated silver chromate solution, the molar solubility of chromate is 6.54 × 10−5. What is the Ksp?
- A saturated lead(II) chloride solution has a chloride concentration of 1.62 × 10−2 mol/L. What is the Ksp?
- From the solubility data given, calculate Ksp for each compound.
- AgI: 2.89 × 10−7 g/100 mL
- SrF2: 1.22 × 10−2 g/100 mL
- Pb(OH)2: 78 mg/500 mL
- BiAsO4: 14.4 mg/2.0 L
- From the solubility data given, calculate Ksp for each compound.
- BaCO3: 10.0 mg/500 mL
- CaF2: 3.50 mg/200 mL
- Mn(OH)2: 6.30 × 10−4 g/300 mL
- Ag2S: 1.60 × 10−13 mg/100 mL
- Given the following solubilities, calculate Ksp for each compound.
- BaCO3: 7.00 × 10−5 mol/L
- CaF2: 1.70 mg/100 mL
- Pb(IO3)2: 2.30 mg/100 mL
- SrC2O4: 1.58 × 10−7mol/L
- Given the following solubilities, calculate Ksp for each compound.
- Ag2SO4: 4.2 × 10−1 g/100 mL
- SrSO4: 1.5 × 10−3 g/100 mL
- CdC2O4: 6.0 × 10−3 g/100 mL
- Ba(IO3)2: 3.96 × 10−2 g/100 mL
- The Ksp of the phosphate fertilizer CaHPO4·2H2O is 2.7 × 10−7 at 25°C. What is the molar concentration of a saturated solution? What mass of this compound will dissolve in 3.0 L of water at this temperature?
- The Ksp of zinc carbonate monohydrate is 5.5 × 10−11 at 25°C. What is the molar concentration of a saturated solution? What mass of this compound will dissolve in 2.0 L of water at this temperature?
- Silver nitrate eye drops were formerly administered to newborn infants to guard against eye infections contracted during birth. Although silver nitrate is highly water soluble, silver sulfate has a Ksp of 1.20 × 10−5 at 25°C. If you add 25.0 mL of 0.015 M AgNO3to 150 mL of 2.8 × 10−3 M Na2SO4, will you get a precipitate? If so, what will its mass be?
- Use the data in Appendix B to predict whether precipitation will occur when each pair of solutions is mixed.
- 150 mL of 0.142 M Ba(NO3)2 with 200 mL of 0.089 M NaF
- 250 mL of 0.079 M K2CrO4 with 175 mL of 0.087 M CaCl2
- 300 mL of 0.109 M MgCl2 with 230 mL of 0.073 M Na2(C2O4)
- What is the maximum volume of 0.048 M Pb(NO3)2 that can be added to 250 mL of 0.10 M NaSCN before precipitation occurs?Ksp = 2.0 × 10−5 for Pb(SCN)2.
- Given 300 mL of a solution that is 0.056 M in lithium nitrate, what mass of solid sodium carbonate can be added before precipitation occurs (assuming that the volume of solution does not change after adding the solid)? Ksp = 8.15 × 10−4 for Li2CO3.
- Given the information in the following table, calculate the molar solubility of each sparingly soluble salt in 0.95 M MgCl2.
| Saturated Solution | Ksp |
| MgCO3·3H2O | 2.4 × 10−6 |
| Mg(OH)2 | 5.6 × 10−12 |
| Mg3(PO4)2 | 1.04 × 10−24 |
Numerical Answers
a. \(K_{sp}=[Cd^{2+}][IO_{3}]^2 \rightarrow 2.5 \times 10^{-8}=x(2x)^{2} \rightarrow 2.5 \times 10^{-8}=4x^{3} \rightarrow x=1.84 \times 10^{-3}\)
b. \(K_{sp}=[Ag^{+}][CN^{-}] \rightarrow 1.6 \times 10^{-14}=(x)(x) \rightarrow x=7.73 \times 10^{-9}\)
c. \(K_{sp}=[Hg^{2+}][I^{-}]^2 \rightarrow 2.9 \times 10^{-29}=(x)(2x)^{2} \rightarrow 1.94\times 10^{-10}\)
2.
a. \(K_{sp}=[Li^{+}]^{3}[PO_{4}^{3-}] \rightarrow 2.37 \times 10^{-11}=(3x)^{3}(x) \rightarrow x=9.68 \times 10^{-4}\)
b. \(K_{sp}=[Ca^{2+}][IO_{3}^{-}]^{2} \rightarrow 6.47 \times 10^{-6}=(x)(2x)^{2} \rightarrow 1.17 \times 10^{-2}\)
c. \(K_{sp}=[Y^{3+}][IO_{3}]^{-}]^{3} \rightarrow 1.12 \times 10^{-10}=(x)(3x)^{3} \rightarrow x=1.42 \times 10^{-3}\)
3. \(0.750\,L \times \frac{0.0144\,mol}{1\,L} \times \frac{311.199\,g}{1\,mol}=3.37\,g\)
\(K_{sp}=[Ag^{+}]^{2}[SO_{4}^{2-}] \rightarrow 1.20 \times 10^{-5}=(2x)^{2}(x) \rightarrow x=0.0144\)
4.
a. \(K_{sp}=[Ag^{+}][Br^{-}] \rightarrow 5.35 \times 10^{-13}=(x)(x) \rightarrow x=7.31 \times 10^{-7}\)
b. \(K_{sp}=[PB^{2+}][C_{2}O_{4}] \rightarrow 8.5 \times 10^{-9}=(x)(x) \rightarrow x=9.2 \times 10^{-5}\)
c. \(K_{sp}=[Fe^{2+}][CO_{3}^{2-}] \rightarrow 3.13 \times 10^{-11}=(x)(x) \rightarrow x=5.60 \times 10^{-6}\)
d. \(K_{sp}=[Ag^{+}]^{3}[PO_{4}^{3-}] \rightarrow 8.89 \times 10^{-17}=(3x)^{3}(x) \rightarrow x=4.26 \times 10^{-5}\)
e. \(K_{sp}=[Cu][CN] \rightarrow 3.47 \times 10^{-20}=(x)(x) \rightarrow x=1.86 \times 10^{-10}\)
5.
a. \(K_{sp}=[Cu][CN] \rightarrow 1.72 \times 10^{-20}=(x)(x) \rightarrow x=4.15 \times 10^{-4}\)
b. \(K_{sp}=[La^{3+}][IO_{3}^{-}]^{3}] \rightarrow 7.50 \times 10^{-12}=(x)(3x)^{3} \rightarrow x=7.26 \times 10^{-4}\)
c. \(K_{sp}=[Mg^{2+}]^{3}[PO_{4}^{3-}]^{2} \rightarrow 1.04 \times 10^{-24}=(3x)^{3}(2x)^{2} \rightarrow x=6.26 \times 10^{-6}\)
d. \(K_{sp}=[Ag^{+}]^{2}[CrO_{4}^{2-}] \rightarrow 1.12 \times 10^{-12}=(2x)^{2}(x) \rightarrow 6.54 \times 10^{-5}\)
e. \(K_{sp}=[Sr^{2+}][SO_{4}^{2-}] \rightarrow 3.44 \times 10^{-7}=(x)(x) \rightarrow x=5.87 \times 10^{-4}\)
6.
\(SiO_{2}\,(g)+H_{2}O\,(l) \rightarrow Si(OH)_{4}\,(aq)\)
\(K_{sp}=[Si^{4+}][OH^{-}]^{4}\)
- 22.4 mg; a secondary reaction occurs, where OH− from the dissociation of the salt reacts with H+ from the dissociation of water. This reaction causes further dissociation of the salt (Le Chatelier’s principle).
\(K_{sp}=[Mg^{2+}][OH^{-}]^{2} \rightarrow 5.61 \times 10^{-12}=(x)(2x)^{2} \rightarrow x=1.12 \times 10^{-4}\)
8.
\(Predicted\,mass: \frac{5.88 \times 10^{-2}\,mol}{1\,L} \times \frac{73.891\,g}{1\,mol} \times 0.5\,L=2.17\,g\)
\(K_{sp}=[Li^{+}]^2[CO_{3}^{2-}] \rightarrow 8.15 \times 10^{-4}=(2x)^{2}(x) \rightarrow x=5.88 \times 10^{-2}\)
The difference between the predicted value and the actual value occurs because the carbonate from the dissociation of the salt reacts with the \(H^{+}\) from the dissociation of water. This reaction causes further dissociation of the salt (Le Chatelier’s principle).
9.
\(K_{sp}=[Ba^{2+}][SO_{4}^{2-}]=(x)(x)=x^{2}=(1.07 \times 10^{-5}\,M)^{2}=1.15 \times 10^{-10}\)
\(BaSO_{4}:(24.6-22.1\,mg) \times \frac{1\,g}{1,000\,mg} \times \frac{1\,mol}{233.38\,g} \times \frac{1}{1.0\,L}=1.07 \times 10^{-5}\,M\)
10. \(K_{sp}=[Ag^{+}]^{2}[CrO_{4}^{2-}]=(2x)^{2}(x)=4x^{3}=4(6.54 \times 10^{-5})=1.12 \times 106{-12}\)
-
\(K_{sp}=[Pb^{2+}][Cl^{-}]^{2}=(x)(2x)^{2}=4x^{3}=4(3.24 \times 10^{-2})^{3}=1.70 \times 10^{-5}\)
-
a. \(K_{sp}=[Ag^{+}][I^{-}]=x^{2}=(1.23 \times 10^{-8})^{2})=1.52 \times 10^{-16}\)
\(AgI: (2.89 \times 10^{-7}\,g \times \frac{1\,mol}{234.77\,g} \times \frac{1}{0.1\,L}=1.23 \times 10^{-8}\)
b. \(K_{sp}=[Sr^{2+}][F^{-}]^{2}]=(x)(2x)^{2}=4x^{3}=4(9.72 \times 10^{-4})^{3}=3.66 \times 10^{-9}\)
\(SrF_{2}=1.22 \times 10^{-2}\,g \times \frac{1\,mol}{125.62\,g} \times \frac{1}{0.1\,L}=9.72 \times 10^{-4}\)
c. \(K_{sp}=[Pb^{2+}][OH^{-}]^{2}=4x^{3}=4(6.47 \times 10^{-4})^{3}=1.08 \times 10^{-9}\)
\(Pb(OH)_{2}=0.078\,g \times \frac{1\,mol}{241.21\,g} \times \frac{1}{0.1\,L}=6.47 \times 10^{-4}\)
d. \(K_{sp}=[Bi^{3+}][AsO_{4}^{3-}]=x^{2}=(2.05 \times 10^{-5})^{2} =4.21 \times 10^{-10}\)
\(BiAsO_{4}=0.0144\,g \times \frac{1\,mol}{350.924\,g} \times \frac{1}{2\,L}=2.05 \times 10^{-5}\)
13.
a. \(K_{sp}=[Ba^{2+}][CO_{3}^{2-}]=x^{2}=(1.01 \times 10^{-4})^{2}=1.03 \times 10^{-8}\)
\(BaCO_{3}:0.01\,g \times \frac{1\,mol}{197.34\,g} \times \frac{1}{0.5\,L}=1.01 \times 10^{-4}\)
b. \(K_{sp}=[Ca^{2+}][F^{-}]^{2}=4x^{3}=4(2.24 \times 10^{-4})^{3}=4.51 \times 10^{-11}\)
\(CaF_{2}: 0.0035\,g \times \frac{1\,mol}{78.07\,g} \times \frac{1}{0.2\,L}=2.24 \times 10^{-4}\)
c. \(K_{sp}=[Mn^{2+}][OH^{-}]^2=4x^{3}=4(2.36 \times 10^{-5})^{3}=5.26 \times 10^{-14}\)
\(Mn(OH)_{2}: 6.30 \times 10^{-4}\,g \times \frac{1\,mol}{88.95\,g} \times \frac{1}{0.3\,L}=2.36 \times 10^{-5}\)
d. \(K_{sp}=[Ag^{+}]^{2}[S^{2-}]=4x^{3}=4(6.46 \times 10^{-18})^{3}=1.08 \times 10^{-51}\)
\(Ag_{2}S: 1.60 \times 10^{-16}\,g \times \frac{1\,mol}{247.8\,g} \times \frac{1}{0.1\,L}=6.46 \times 10^{-18}\)
14.
a. \(K_{sp}=[Ba^{2+}][CO_{3}^{2-}]=x^{2}=(7.0 \times 10^{-5})^{2}=4.90 \times 10^{-9}\)
b. \(K_{sp}=[Ca^{2+}][F^{-}]^{2}=4x^{3}=4(2.18 \times 10^{-4})^{3}=4.13 \times 10^{-11}\)
\(CaF_{2}: 0.0017\,g \times \frac{1\,mol}{78.07\,g} \times \frac{1}{0.1\,L}=2.18 \times 10^{-4}\)
c. \(K_{sp}=[Pb^{2+}][IO_{3}^{-}]^{2}=4x^{3}=4(4.13 \times 10^{-5})^{3}=2.82 \times 10^{-13}\)
\(Pb(IO_{3})_{2}: 0.0023\,g \times \frac{1\,mol}{557.0053\,g} \times \frac{1}{0.1\,L}=4.13 \times 10^{-5}\)
d. \(K_{sp}=[Sr^{2+}][C_2O_4^{2-}]=x^{2}=(1.58 \times 10^{-7})^{2}=2.50 \times 10^{-14}\)
a. \(K_{sp}=[Ag^{+}]^{2}[SO_{4}]^{2-}=4x^{3}=4(1.35 \times 10^{-2})^{3}=9.8 \times 10^{-6}\)
\(Ag_{2}SO_{4}: 4.2 \times 10^{-1}\,g \times \frac{1\,mol}{311.799\,g} \times \frac{1}{0.1\,L}=1.35 \times 10^{-2}\)
b. \(K_{sp}=[Sr^{2+}][SO_{4}^{2-}]=x^{2}=(8.17 \times 10^{-5})^{2}=6.7 \times 10^{-9}\)
\(SrSO_{4}: 1.5 \times 10^{-3}\,g \times \frac{1\,mol}{183.68\,g} \times \frac{1}{0.1\,L}=8.17 \times 10^{-5}\)
c. \(K_{sp}=[Cd^{2+}][C_2O_4^{2-}]=x^{2}=(2.99 \times 10^{-4})^{2}=8.9 \times 10^{-8}\)
\(CdC_{2}O_{4}: 6.0 \times 10^{-3}\,g \times \frac{1\,mol}{200.43\,g} \times \frac{1}{0.1\,L}=2.99 \times 10^{-4}\)
d. \(K_{sp}=[Ba^{2+}][IO_{3}^{-}]^{2}=4x^{3}=4(8.13 \times 10^{-4})^{3}=2.15 \times 10^{-9}\)
\(Ba(IO_{3})_{2}: 3.96 \times 10^{-2}\,g \times \frac{1\,mol}{487.15\,g} \times \frac{1}{0.1\,L}=8.13 \times 10^{-4}\)
16.
\(K_{sp}=[Ca^{2+}][HPO_{4}^{2-}] \rightarrow 2.7 \times 10^{-7}=x^{2} \rightarrow x=5.2 \times 10^{-4}\)
\(CaHPO4·2H2O: 3.0\,L \times \frac{2.7 \times 10^{-7}\,mol}{1\,L} \times \frac{290.1299\,g}{1\,mol}=2.35 \times 10^{-4}\,g\)
17.
\(K_{sp}=[Zn^{2+}][CO_{3}^{2+}] \rightarrow 5.5 \times 10^{-11}=x^{2} \rightarrow x=7.4 \times 10^{-6}\)
2.1 mg
18. \(Q=[Ag^{+}]^{2}[SO_{4}^{2-}]=(2.14 \times 10^{-3})^{2} \times 2.4 \times 10^{-3}=1.1 \times 10^{-8}<1.20 \times 10^{-5}\) Therefore, no precipitate will form.
\(Ag^{+}: \frac{(0.025\,L)(0.015\,M)}{0.175\,L}=2.14 \times 10^{-3}\)
\(SO_{4}^{2-}: \frac{(0.15\,L)(2.8 \times 10^{-3}}{0.175\,L}=2.4 \times 10^{-3}\)
19.
a. \(Q=[Ba^{2+}][F^{-}]^{2}=(0.060857)(0.05643)^{2}=1.94 \times 10^{-4}>1.84 \times 10^{-7}\) Therefore, precipitate will form.
\(Ba^{2+}: \frac{(0.150)(0.142)}{0.35}=0.060857\)
\(F^{-}: \frac{(0.25)(0.079)}{0.35}=0.05643\)
b. \(Q=[K^{+}][Cl^{-}]=(0.0465)(0.0358)=1.66 \times 10^{-3}<21.7. Therefore, precipitate will not form.
\(K^{+}: \frac{(0.25)(0.079)}{0.425}=0.0465\)
\(Cl^{-}: \frac{(0.175)(0.087)}{0.425}=0.0358\)
c. \(Q=[Mg^{2+}][C_{2}O_{4}^{2-}]=(0.0617)(0.0317)=1.95 \times 10^{-3}>8.5 \times 10^{-5}\) Therefore, precipitate will form.
\(Mg^{2+}:\frac{(0.3)(0.109)}{0.53}=0.0617\)
\(C_{2}O_{4}: \frac{(0.23)(0.073)}{0.53}=0.0317\)
20. 520 mL
- 8.27 g
-
a. \(K_{sp}=\sqrt{2.4 \times 10^{-6}}=1.55 \times 10^{-3}\)
b. \(K_{sp}=(\frac{5.6 \times 10^{-12}}{4})^{\frac{1}{3}}=1.12 \times 10^{-4}\)
c. \(K_{sp}=(\frac{1.04 \times 10^{-24}}{108})^{\frac{1}{5}}=6.26 \times 10^{-6}\)
17.5: Factors that Affect Solubility
Conceptual Problems
- Do you expect the actual molar solubility of LaPO4 to be greater than, the same as, or less than the value calculated from its Ksp? Explain your reasoning.
- Do you expect the difference between the calculated molar solubility and the actual molar solubility of Ca3(PO4)2 to be greater than or less than the difference in the solubilities of Mg3(PO4)2? Why?
- Write chemical equations to describe the interactions in a solution that contains Mg(OH)2, which forms ion pairs, and in one that contains propanoic acid (CH3CH2CO2H), which forms a hydrated neutral molecule.
- Draw representations of Ca(IO3)2 in solution
- as an ionic solid.
- in the form of ion pairs.
- as discrete ions.
Conceptual Answers
1. It is expected that the molar solubility of \LaPO_{4}\) be less than the value from its \(K_{sp}\) because the \(K_{sp}=[La^{3+}][PO_{4}^{3-}]=x^{2}\) in which the molar solubility would be the square root of of \(K_{sp}\).
2. It would be expected that there would be no difference in the calculated molar solubility and actual molar solubility of \(Ca_{3}(PO_{4})_{2}\) and \(Mg_{3}(PO_{4})_{2}\) follow the similar equation: \(K_{sp}=108x^{5}\) . It would ultimately depend on the K_{sp} values as \(x=(\frac{K_{sp}}{108})^{\frac{1}{5}} in which the larger \(K_{sp} gives the larger molar solubility.
3.
\(Mg(OH)_{2}\,(s) \rightleftharpoons Mg^{2+}\,(aq)+2\,OH^{-}\,(aq)\)
\(CH_{3}CH_{2}CO_{2}H\,(aq) \rightleftharpoons CH_{3}CH_{2}CO_{2}^{-}\,(aq)+H^{+}\,(aq)\)
Numerical Problem
- Ferric phosphate has a molar solubility of 5.44 × 10−16 in 1.82 M Na3PO4. Predict its Ksp. The actual Ksp is 1.3 × 10−22. Explain this discrepancy.
Numerical Answer
- 9.90 × 10−16; the solubility is much higher than predicted by Ksp due to the formation of ion pairs (and/or phosphate complexes) in the sodium phosphate solution.
17.6: Precipitation and Separation of Ions
Questions
- Iron(II) hydroxide is only sparingly soluble in water at 25oC; its Ksp is \(7.9 \times 10^{-16}\). Calculate the solubility of iron(II) hydroxide in a buffer solution with pH = 7.00.
- A solution contains 0.60 M \(\ce{Ba^2+}\) and 0.30 M \(\ce{Ca^2+}\); Ksp values for \(\ce{BaCrO4}\) and \(\ce{CaCrO4}\) are \(1.2 \times 10^{-10}\) and \(7.1 \times 10^{-4}\) respectively. What value of \(\ce{[CrO4^2- ]}\) will result in a maximum separation of these two ions?
- A solution contains 0.60 M \(\ce{Ba^2+}\) and 0.30 M \(\ce{Ca^2+}\); Ksp values for \(\ce{BaCrO4}\) and \(\ce{CaCrO4}\) are \(1.2 \times 10^{-10}\) and \(7.1 \times 10^{-4}\) respectively. Calculate the \(\ce{[Ca^2+]/[Ba^2+]}\) ratio in the solution when \(\ce{[CrO4^2- ]}\) is maintained at \(1.2 \times 10^{-3}\; M\).
Solutions
- Answer \(\ce{[Fe^2+]} = \textrm{0.079 M}\)
Consider...
\(\ce{[OH- ]} = 10^{(-14+7)} = \textrm{1.00e-7 (buffer)}\).
\(\ce{[Fe^2+]} (\textrm{1.00e-7})^2 = K_{\ce{sp}}\); \(\ce{[Fe^2+]} =\: ?\)
This \(\ce{Fe^2+}\) concentration is low; it is not very soluble in a neutral solution (pH = 7).
What is \(\ce{[Fe^2+]}\) in a solution whose pH = 6.00? - Answer \(\ce{[CrO4^2- ]} = \textrm{2.37e-3 M}\)
Consider...
Solid \(\ce{BaCrO4}\) will form first as \(\ce{[CrO4^2- ]}\) increases. The maximum \(\ce{[CrO4^2- ]}\) to precipitate \(\ce{CaCrO4}\) is estimated as follows.
\(\ce{[CrO4^2- ]} = \dfrac{\textrm{7.1e-4}}{0.30} = \textrm{2.37e-3 M}\)
Estimate \(\ce{[Ba^2+]}\) when \(\ce{[CrO4^2- ]} = \textrm{2.3e-3 M}\), slightly below the maximum concentration. - Answer \(\ce{\dfrac{[Ca^2+]}{[Ba^2+]}} = \textrm{3e6}\)
Consider...
\(\ce{[Ba^2+]} = \dfrac{\textrm{1.2e-10}}{\textrm{1.2e-3}} = \textrm{1e-7}\);
\(\ce{\dfrac{[Ca^2+]}{[Ba^2+]}} = \dfrac{0.3}{\textrm{1e-7}} =\: ?\) The ratio of three million is large!
17.7: Qualitative Analysis for Metallic Elements
Conceptual Problem
- Given a solution that contains a mixture of \(NaCl\), \(CuCl_{2}\), and \(ZnCl_{2}\), propose a method for separating the metal ions.
Conceptual Solution
1. Given a solution that contains a mixture of \(NaCl\), \(CuCl_{2}\), and \(ZnCl_{2}\), we can first use \(H_{2}S\) to separate the \(Zn^{2+}\) through filtration, then use \(ZnS\) to separate the \(Cu^{2+}\) through filtration, and be left with \(Na^{+}\).

