16.4: The pH Scale
- Page ID
- 25228
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To define the pH scale as a measure of acidity of a solution
Because of its amphoteric nature (i.e., acts as both an acid or a base), water does not always remain as \(H_2O\) molecules. In fact, two water molecules react to form hydronium and hydroxide ions:
\[ 2\, H_2O \;(l) \rightleftharpoons H_3O^+ \;(aq) + OH^− \; (aq) \label{1} \]
This is also called the self-ionization of water. The concentration of \(H_3O^+\) and \(OH^-\) are equal in pure water because of the 1:1 stoichiometric ratio of Equation 1. The molarity of H3O+ and OH- in water are also both \(1.0 \times 10^{-7} \,M\) at 25° C. Therefore, a constant of water (\(K_w\)) is created to show the equilibrium condition for the self-ionization of water. The product of the molarity of hydronium and hydroxide ion is always \(1.0 \times 10^{-14}\).
\[K_w= [H_3O^+][OH^-] = 1.0 \times 10^{-14} \label{2} \]
This equations also applies to all aqueous solutions. However, \(K_w\) does change at different temperatures, which affects the pH range discussed below.
\(H^+\) and \(H_3O^+\) is often used interchangeably to represent the hydrated proton, commonly call the hydronium ion.
The equation for water equilibrium is:
\[ H_2O \rightleftharpoons H^+ + OH^- \label{3} \]
- If an acid (\(H^+\)) is added to the water, the equilibrium shifts to the left and the \(OH^-\) ion concentration decreases
- If base ( \(OH^-\)) is added to water, the equilibrium shifts to left and the \(H^+\) concentration decreases.
pH and pOH
The constant of water determines the range of the pH scale. To understand what the pKw is, it is important to understand first what the "p" means in pOH, and pH. The Danish biochemist Søren Sørenson proposed the term pH to refer to the "potential of hydrogen ion." He defined the "p" as the negative of the logarithm, -log, of [H+]. Therefore the pH is the negative logarithm of the molarity of H. The pOH is the negative logarithm of the molarity of OH- and the pKw is the negative logarithm of the constant of water. These definitions give the following equations:
\[pH= -\log [H^+] \label{4a} \]
\[pOH= -\log [OH^-] \label{4b} \]
\[pK_w= -\log [K_w] \label{4c} \]
At room temperature (25 °C),
\[K_w =1.0 \times 10^{-14} \label{4d} \]
So
\[pK_w=-\log [1.0 \times 10^{-14}] \label{4e} \]
Using the properties of logarithms, Equation \(\ref{4e}\) can be rewritten as
\[10^{-pK_w}=10^{-14}. \label{4f} \]
By substituting, we see that pKw is 14. The equation also shows that each increasing unit on the scale decreases by the factor of ten on the concentration of \(H^+\). For example, a pH of 1 has a molarity ten times more concentrated than a solution of pH 2.
Since
\[pK_w\ = 14 \label{5a} \]
\[pK_w= pH + pOH = 14 \label{5b} \]
- A solution with more \(OH^-\) ions than \(H^+\) ion is basic; for aqueous solutions at 25°C that corresponds to pH > 7.
- A solution with more \(H^+\) ions than \(OH^-\) ions is acidic; for aqueous solutions at 25°C that corresponds to pH < 7.
- A solution with that same concentration of \(H^+\) ions than \(OH^-\) ions is neutral; for aqueous solutions at 25°C that corresponds to pH = 7.
Since the autoionization constant \(K_w\) is temperature dependent, these correlations between pH values and the acidic/neutral/basic adjectives will be different at temperatures other than 25 °C. For example, the hydronium molarity of pure water at 80 °C is 4.9 × 10−7 M, which corresponds to pH and pOH values of:
\[\mathrm{pH=-\log[H_3O^+]=-\log(4.9\times 10^{−7})=6.31}\label{12} \]
\[\mathrm{pOH=-\log[OH^-]=-\log(4.9\times 10^{−7})=6.31}\label{13} \]
At this temperature, then, neutral solutions exhibit pH = pOH = 6.31, acidic solutions exhibit pH less than 6.31 and pOH greater than 6.31, whereas basic solutions exhibit pH greater than 6.31 and pOH less than 6.31. This distinction can be important when studying certain processes that occur at nonstandard temperatures, such as enzyme reactions in warm-blooded organisms. Unless otherwise noted, references to pH values are presumed to be those at standard temperature (25 °C) (Table \(\PageIndex{1}\)).
The pH scale is logarithmic, meaning that an increase or decrease of an integer value changes the concentration by a tenfold. For example, a pH of 3 is ten times more acidic than a pH of 4. Likewise, a pH of 3 is one hundred times more acidic than a pH of 5. Similarly a pH of 11 is ten times more basic than a pH of 10.
Figure \(\PageIndex{1}\) depicts the pH scale with common solutions and where they are on the scale.
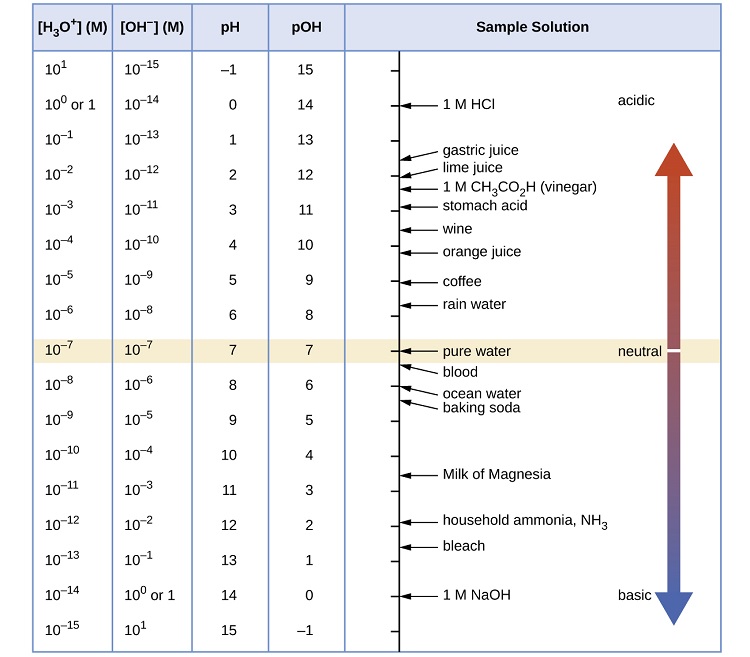
It is common that the pH scale is argued to range from 0-14 or perhaps 1-14, but neither is correct. The pH range does not have an upper nor lower bound, since as defined above, the pH is an indication of concentration of H+. For example, at a pH of zero the hydronium ion concentration is one molar, while at pH 14 the hydroxide ion concentration is one molar. Typically the concentrations of H+ in water in most solutions fall between a range of 1 M (pH=0) and 10-14 M (pH=14). Hence a range of 0 to 14 provides sensible (but not absolute) "bookends" for the scale. One can go somewhat below zero and somewhat above 14 in water, because the concentrations of hydronium ions or hydroxide ions can exceed one molar.
If the concentration of \(NaOH\) in a solution is \(2.5 \times 10^{-4}\; M\), what is the concentration of \(H_3O^+\)?
Solution
Because
\[1.0 \times 10^{-14} = [H_3O^+][OH^-] \nonumber \]
to find the concentration of H3O+, solve for the [H3O+].
\[\dfrac{1.0 \times 10^{-14}}{[OH^-]} = [H_3O^+] \nonumber \]
\[\dfrac{1.0 \times 10^{-14}}{2.5 \times 10^{-4}} = [H_3O^+] = 4.0 \times 10^{-11}\; M \nonumber \]
- Find the pH of a solution of 0.002 M of HCl.
- Find the pH of a solution of 0.00005 M NaOH.
Solution
- The equation for pH is -log [H+]
\[[H^+]= 2.0 \times 10^{-3}\; M \nonumber \]
\[pH = -\log [2.0 \times 10^{-3}] = 2.70 \nonumber \]
- The equation for pOH is -log [OH-]
\[ [OH^-]= 5.0 \times 10^{-5}\; M \nonumber \]
\[pOH = -\log [5.0 \times 10^{-5}] = 4.30 \nonumber \]
\[pK_w = pH + pOH \nonumber \]
and
\[pH = pK_w - pOH \nonumber \]
then
\[pH = 14 - 4.30 = 9.70 \nonumber \]
If moist soil has a pH of 7.84, what is the H+ concentration of the soil solution?
Solution
\[pH = -\log [H^+] \nonumber \]
\[7.84 = -\log [H^+] \nonumber \]
\[[H^+] = 1.45 \times 10^{-8} M \nonumber \]
Hint: Place -7.84 in your calculator and take the antilog (often inverse log or 10x) = 1.45 x 10-8M
A Video Introduction to pH: Introduction to pH [youtu.be]
Summary
The concentration of hydronium ion in a solution of an acid in water is greater than \( 1.0 \times 10^{-7}\; M\) at 25 °C. The concentration of hydroxide ion in a solution of a base in water is greater than \( 1.0 \times 10^{-7}\; M\) at 25 °C. The concentration of H3O+ in a solution can be expressed as the pH of the solution; \(\ce{pH} = -\log \ce{H3O+}\). The concentration of OH− can be expressed as the pOH of the solution: \(\ce{pOH} = -\log[\ce{OH-}]\). In pure water, pH = 7.00 and pOH = 7.00.
References
- Petrucci, et al. "Self-Ionization of Water and the pH Scale." General Chemistry: Principles & Modern Applications. 7th ed. Upper Saddle River: Pearson Prentice Hall, 2007. 669-71.
- Segel, Irwin H. "Acid and Base." Biochemical Calculations. 2nd ed. Wiley: BK Book, 1976. 12.
- Christopher G. McCarty and Ed Vitz, Journal of Chemical Education, 83(5), 752 (2006)
Contributors and Attributions
- Emmellin Tung (UCD), Sharon Tsao (UCD), Divya Singh (UCD), Patrick Gormley (Lapeer Community School District)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

