8.2: Ionic Bonding
- Page ID
- 21746
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To describe the characteristics of ionic bonding.
- To quantitatively describe the energetic factors involved in the formation of an ionic bond.
Ions are atoms or molecules which are electrically charged. Cations are positively charged and anions carry a negative charge. Ions form when atoms gain or lose electrons. Since electrons are negatively charged, an atom that loses one or more electrons will become positively charged; an atom that gains one or more electrons becomes negatively charged. Ionic bonding is the attraction between positively- and negatively-charged ions. These oppositely charged ions attract each other to form ionic networks (or lattices). Electrostatics explains why this happens: opposite charges attract and like charges repel. When many ions attract each other, they form large, ordered, crystal lattices in which each ion is surrounded by ions of the opposite charge. Generally, when metals react with non-metals, electrons are transferred from the metals to the non-metals. The metals form positively-charged ions and the non-metals form negatively-charged ions.
Generating Ionic Bonds
Ionic bonds form when metals and non-metals chemically react. By definition, a metal is relatively stable if it loses electrons to form a complete valence shell and becomes positively charged. Likewise, a non-metal becomes stable by gaining electrons to complete its valence shell and become negatively charged. When metals and non-metals react, the metals lose electrons by transferring them to the non-metals, which gain them. Consequently, ions are formed, which instantly attract each other—ionic bonding.
In the overall ionic compound, positive and negative charges must be balanced, because electrons cannot be created or destroyed, only transferred. Thus, the total number of electrons lost by the cationic species must equal the total number of electrons gained by the anionic species.
For example, in the reaction of Na (sodium) and Cl (chlorine), each Cl atom takes one electron from a Na atom. Therefore each Na becomes a Na+ cation and each Cl atom becomes a Cl- anion. Due to their opposite charges, they attract each other to form an ionic lattice. The formula (ratio of positive to negative ions) in the lattice is \(\ce{NaCl}\).
\[\ce{2Na (s) + Cl 2(g) \rightarrow 2NaCl (s)} \nonumber \]
These ions are arranged in solid NaCl in a regular three-dimensional arrangement (or lattice):
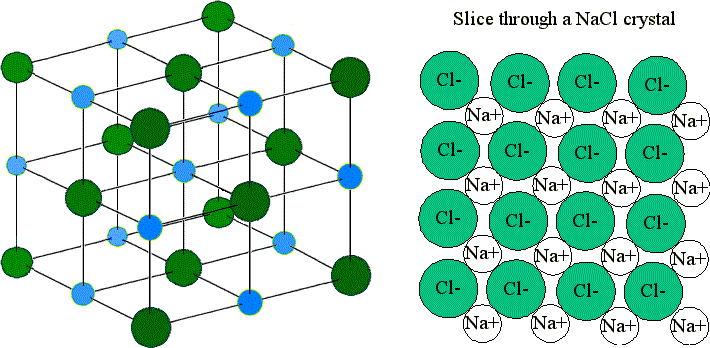
NaCl lattice. (left) 3-D structure and (right) simple 2D slice through lattes. Images used with permission from Wikipedia and Mike Blaber.
The chlorine has a high affinity for electrons, and the sodium has a low ionization energy. Thus the chlorine gains an electron from the sodium atom. This can be represented using ewis dot symbols (here we will consider one chlorine atom, rather than Cl2):
The arrow indicates the transfer of the electron from sodium to chlorine to form the Na+ metal ion and the Cl- chloride ion. Each ion now has an octet of electrons in its valence shell:
- Na+: 2s22p6
- Cl-: 3s23p6
Energetics of Ionic Bond Formation
Ionic bonds are formed when positively and negatively charged ions are held together by electrostatic forces. Consider a single pair of ions, one cation and one anion. How strong will the force of their attraction be? According to Coulomb's Law, the energy of the electrostatic attraction (\(E\)) between two charged particles is proportional to the magnitude of the charges and inversely proportional to the internuclear distance between the particles (\(r\)):
\[E \propto \dfrac{Q_{1}Q_{2}}{r} \label{Eq1a} \]
\[ E = k\dfrac{Q_{1}Q_{2}}{r} \label{Eq1b} \]
where each ion’s charge is represented by the symbol Q. The proportionality constant k is equal to 2.31 × 10−28 J·m. This value of k includes the charge of a single electron (1.6022 × 10−19 C) for each ion. The equation can also be written using the charge of each ion, expressed in coulombs (C), incorporated in the constant. In this case, the proportionality constant, k, equals 8.999 × 109 J·m/C2. In the example given, Q1 = +1(1.6022 × 10−19 C) and Q2 = −1(1.6022 × 10−19 C). If Q1 and Q2 have opposite signs (as in NaCl, for example, where Q1 is +1 for Na+ and Q2 is −1 for Cl−), then E is negative, which means that energy is released when oppositely charged ions are brought together from an infinite distance to form an isolated ion pair.
Energy is always released when a bond is formed and correspondingly, it always requires energy to break a bond.
As shown by the green curve in the lower half of Figure \(\PageIndex{1}\), the maximum energy would be released when the ions are infinitely close to each other, at r = 0. Because ions occupy space and have a structure with the positive nucleus being surrounded by electrons, however, they cannot be infinitely close together. At very short distances, repulsive electron–electron interactions between electrons on adjacent ions become stronger than the attractive interactions between ions with opposite charges, as shown by the red curve in the upper half of Figure \(\PageIndex{1}\). The total energy of the system is a balance between the attractive and repulsive interactions. The purple curve in Figure \(\PageIndex{1}\) shows that the total energy of the system reaches a minimum at r0, the point where the electrostatic repulsions and attractions are exactly balanced. This distance is the same as the experimentally measured bond distance.
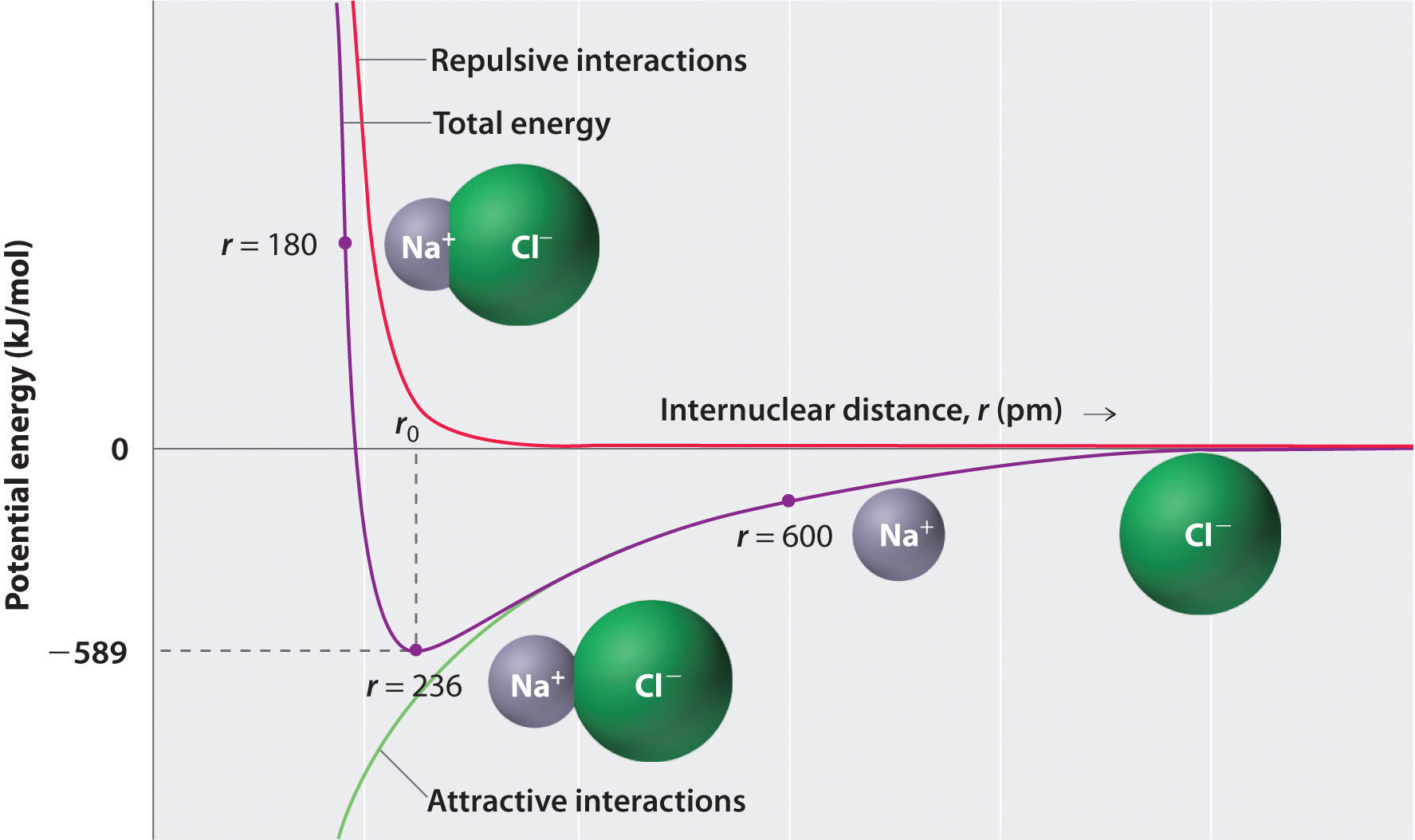
Consider the energy released when a gaseous \(Na^+\) ion and a gaseous \(Cl^-\) ion are brought together from r = ∞ to r = r0. Given that the observed gas-phase internuclear distance is 236 pm, the energy change associated with the formation of an ion pair from an \(Na^+_{(g)}\) ion and a \(Cl^-_{(g)}\) ion is as follows:
\[ \begin{align*} E &= k\dfrac{Q_{1}Q_{2}}{r_{0}} \\[4pt] &= (2.31 \times {10^{ - 28}}\rm{J}\cdot \cancel{m} ) \left( \dfrac{( + 1)( - 1)}{236\; \cancel{pm} \times 10^{ - 12} \cancel{m/pm}} \right) \\[4pt] &= - 9.79 \times 10^{ - 19}\; J/ion\; pair \label{Eq2} \end{align*} \]
The negative value indicates that energy is released. Our convention is that if a chemical process provides energy to the outside world, the energy change is negative. If it requires energy, the energy change is positive. To calculate the energy change in the formation of a mole of NaCl pairs, we need to multiply the energy per ion pair by Avogadro’s number:
\[ E=\left ( -9.79 \times 10^{ - 19}\; J/ \cancel{ion pair} \right )\left ( 6.022 \times 10^{ 23}\; \cancel{ion\; pair}/mol\right )=-589\; kJ/mol \label{Eq3} \]
This is the energy released when 1 mol of gaseous ion pairs is formed, not when 1 mol of positive and negative ions condenses to form a crystalline lattice. Because of long-range interactions in the lattice structure, this energy does not correspond directly to the lattice energy of the crystalline solid. However, the large negative value indicates that bringing positive and negative ions together is energetically very favorable, whether an ion pair or a crystalline lattice is formed.
We summarize the important points about ionic bonding:
- At r0, the ions are more stable (have a lower potential energy) than they are at an infinite internuclear distance. When oppositely charged ions are brought together from r = ∞ to r = r0, the energy of the system is lowered (energy is released).
- Because of the low potential energy at r0, energy must be added to the system to separate the ions. The amount of energy needed is the bond energy.
- The energy of the system reaches a minimum at a particular internuclear distance (the bond distance).
Calculate the amount of energy released when 1 mol of gaseous Li+F− ion pairs is formed from the separated ions. The observed internuclear distance in the gas phase is 156 pm.
Given: cation and anion, amount, and internuclear distance
Asked for: energy released from formation of gaseous ion pairs
Strategy:
Substitute the appropriate values into Equation \(\ref{Eq1b}\) to obtain the energy released in the formation of a single ion pair and then multiply this value by Avogadro’s number to obtain the energy released per mole.
Solution:
Inserting the values for Li+F− into Equation \(\ref{Eq1b}\) (where Q1 = +1, Q2 = −1, and r = 156 pm), we find that the energy associated with the formation of a single pair of Li+F− ions is
\[ \begin{align*} E &=k \dfrac{Q_1Q_2}{r_0} \\[4pt] &=\left(2.31 \times 10^{−28} J⋅\cancel{m} \right) \left(\dfrac{\text{(+1)(−1)}}{156\; pm \times 10^{−12} \cancel{m/pm}} \right)\\[4pt] &=−1.48 \times 10^{−18} \end{align*} \nonumber \]
Then the energy released per mole of Li+F− ion pairs is
\[ \begin{align*} E&= \left(−1.48 \times 10^{−18} J/ \cancel{\text{ion pair}}\right) \left(6.022 \times 10^{23} \cancel{\text{ion pair}}/mol\right)\\[4pt] &−891 \;kJ/mol \end{align*} \nonumber \]
Because Li+ and F− are smaller than Na+ and Cl− (see Section 7.3), the internuclear distance in LiF is shorter than in NaCl. Consequently, in accordance with Equation \(\ref{Eq1b}\), much more energy is released when 1 mol of gaseous Li+F− ion pairs is formed (−891 kJ/mol) than when 1 mol of gaseous Na+Cl− ion pairs is formed (−589 kJ/mol).
Calculate the amount of energy released when 1 mol of gaseous \(\ce{MgO}\) ion pairs is formed from the separated ions. The internuclear distance in the gas phase is 175 pm.
- Answer
-
−3180 kJ/mol = −3.18 × 103 kJ/mol
Electron Configuration of Ions
How does the energy released in lattice formation compare to the energy required to strip away a second electron from the Na+ ion? Since the Na+ ion has a noble gas electron configuration, stripping away the next electron from this stable arrangement would require more energy than what is released during lattice formation (Sodium I2 = 4,560 kJ/mol). Thus, sodium is present in ionic compounds as Na+ and not Na2+. Likewise, adding an electron to fill a valence shell (and achieve noble gas electron configuration) is exothermic or only slightly endothermic. To add an additional electron into a new subshell requires tremendous energy - more than the lattice energy. Thus, we find Cl- in ionic compounds, but not Cl2-.
| Compound | Lattice Energy (kJ/mol) |
|---|---|
| LiF | 1024 |
| LiI | 744 |
| NaF | 911 |
| NaCl | 788 |
| NaI | 693 |
| KF | 815 |
| KBr | 682 |
| KI | 641 |
| MgF2 | 2910 |
| SrCl2 | 2130 |
| MgO | 3938 |
This amount of energy can compensate for values as large as I3 for valence electrons (i.e. can strip away up to 3 valence electrons). Because most transition metals would require the removal of more than 3 electrons to attain a noble gas core, they are not found in ionic compounds with a noble gas core. A transition metal always loses electrons first from the higher 's' subshell, before losing from the underlying 'd' subshell. (The remaining electrons in the unfilled d subshell are the reason for the bright colors observed in many transition metal compounds!) For example, iron ions will not form a noble gas core:
- Fe: [Ar]4s23d6
- Fe2+: [Ar] 3d6
- Fe3+: [Ar] 3d5
Some metal ions can form a pseudo noble gas core (and be colorless), for example:
- Ag: [Kr]5s14d10 Ag+ [Kr]4d10 Compound: AgCl
- Cd: [Kr]5s24d10 Cd2+ [Kr]4d10 Compound: CdS
The valence electrons do not adhere to the "octet rule" in this case (a limitation of the usefulness of this rule). Note: The silver and cadmium atoms lost the 5s electrons in achieving the ionic state.
When a positive ion is formed from an atom, electrons are always lost first from the subshell with the largest principle quantum number
Polyatomic Ions
Not all ionic compounds are formed from only two elements. Many polyatomic ions exist, in which two or more atoms are bound together by covalent bonds. They form a stable grouping which carries a charge (positive or negative). The group of atoms as a whole acts as a charged species in forming an ionic compound with an oppositely charged ion. Polyatomic ions may be either positive or negative, for example:
- NH4+ (ammonium) = cation
- SO42- (sulfate) = anion
The principles of ionic bonding with polyatomic ions are the same as those with monatomic ions. Oppositely charged ions come together to form a crystalline lattice, releasing a lattice energy. Based on the shapes and charges of the polyatomic ions, these compounds may form crystalline lattices with interesting and complex structures.
Summary
The amount of energy needed to separate a gaseous ion pair is its bond energy. The formation of ionic compounds are usually extremely exothermic. The strength of the electrostatic attraction between ions with opposite charges is directly proportional to the magnitude of the charges on the ions and inversely proportional to the internuclear distance. The total energy of the system is a balance between the repulsive interactions between electrons on adjacent ions and the attractive interactions between ions with opposite charges.
Contributors and Attributions
- Wikibooks [en.wikibooks.org]
Modified by Joshua Halpern (Howard University)

