7.5: Electron Affinities
- Page ID
- 21741
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To master the concept of electron affinity as a measure of the energy required to add an electron to an atom or ion.
- To recognize the inverse relationship of ionization energies and electron affinities
The electron affinity (\(EA\)) of an element \(E\) is defined as the energy change that occurs when an electron is added to a gaseous atom or ion:
\[ E_{(g)}+e^- \rightarrow E^-_{(g)} \;\;\; \text{energy change=}EA \label{7.5.1} \]
Unlike ionization energies, which are always positive for a neutral atom because energy is required to remove an electron, electron affinities can be negative (energy is released when an electron is added), positive (energy must be added to the system to produce an anion), or zero (the process is energetically neutral). This sign convention is consistent with a negative value corresponded to the energy change for an exothermic process, which is one in which heat is released (Figure \(\PageIndex{1}\)).
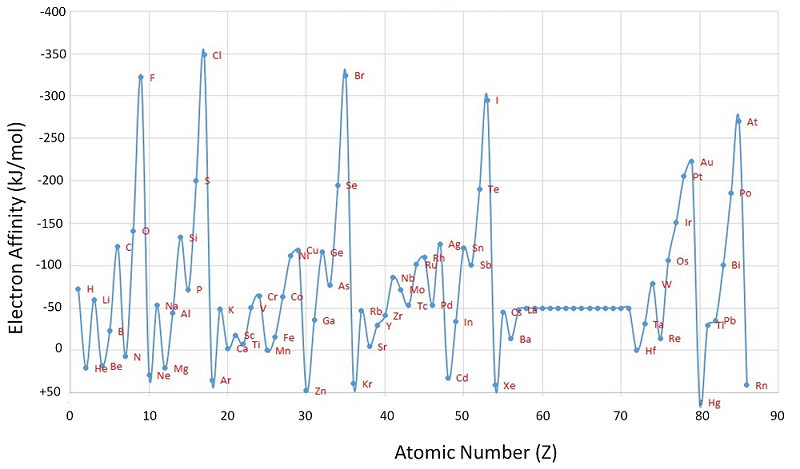
The chlorine atom has the most negative electron affinity of any element, which means that more energy is released when an electron is added to a gaseous chlorine atom than to an atom of any other element:
\[ \ce{ Cl(g) + e^- \rightarrow Cl^- (g)} \;\;\; EA=-346\; kJ/mol \label{7.5.2} \]
In contrast, beryllium does not form a stable anion, so its effective electron affinity is
\[ \ce{ Be(g) + e^- \rightarrow Be^- (g)} \;\;\; EA \ge 0 \label{7.5.3} \]
Nitrogen is unique in that it has an electron affinity of approximately zero. Adding an electron neither releases nor requires a significant amount of energy:
\[ \ce{ N(g) + e^- \rightarrow N^- (g)} \;\;\; EA \approx 0 \label{7.5.4} \]
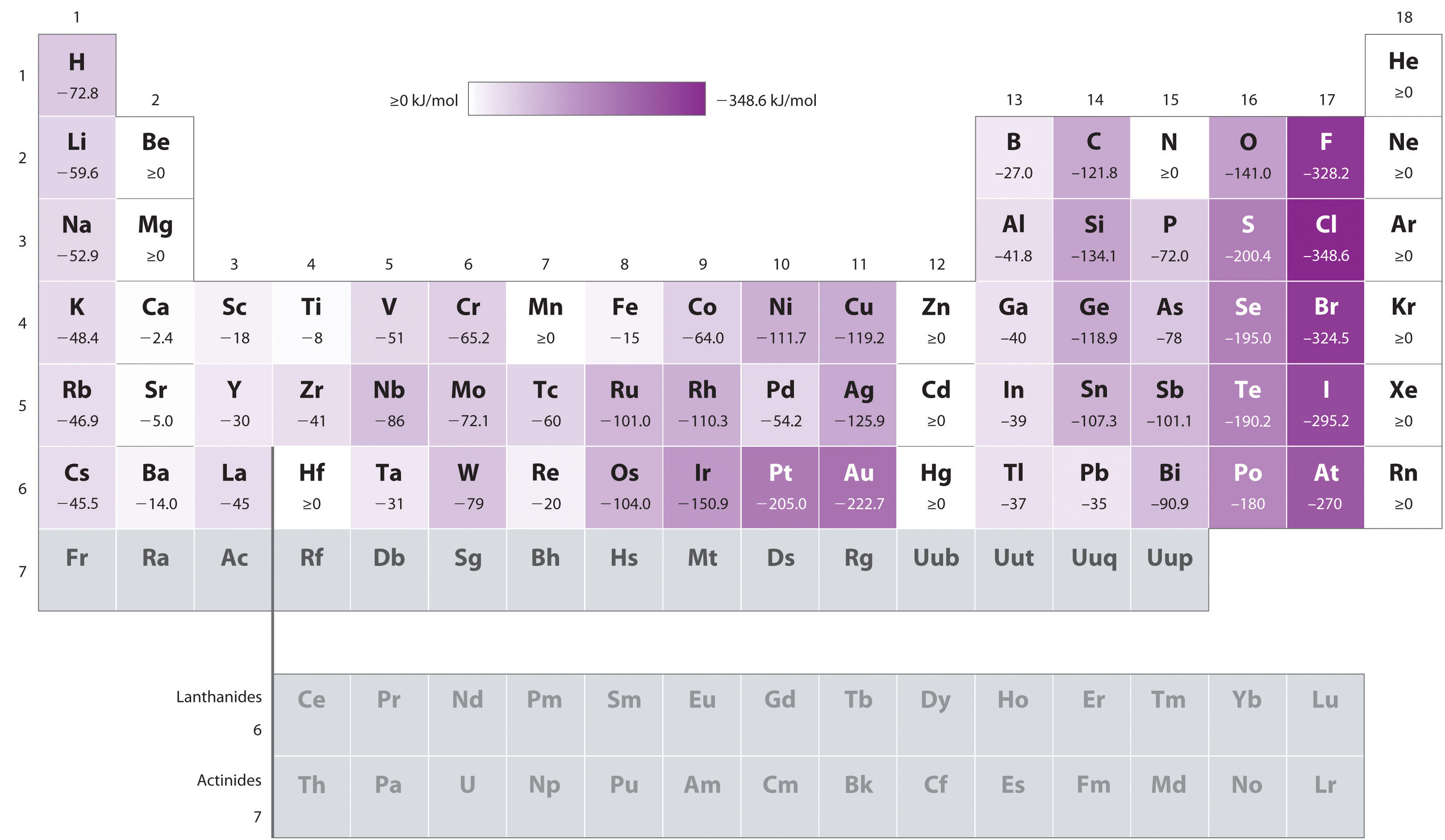
Generally, electron affinities become more negative across a row of the periodic table.
In general, electron affinities of the main-group elements become less negative as we proceed down a column. This is because as n increases, the extra electrons enter orbitals that are increasingly far from the nucleus.
Atoms with the largest radii, which have the lowest ionization energies (affinity for their own valence electrons), also have the lowest affinity for an added electron. There are, however, two major exceptions to this trend:
- The electron affinities of elements B through F in the second row of the periodic table are less negative than those of the elements immediately below them in the third row. Apparently, the increased electron–electron repulsions experienced by electrons confined to the relatively small 2p orbitals overcome the increased electron–nucleus attraction at short nuclear distances. Fluorine, therefore, has a lower affinity for an added electron than does chlorine. Consequently, the elements of the third row (n = 3) have the most negative electron affinities. Farther down a column, the attraction for an added electron decreases because the electron is entering an orbital more distant from the nucleus. Electron–electron repulsions also decrease because the valence electrons occupy a greater volume of space. These effects tend to cancel one another, so the changes in electron affinity within a family are much smaller than the changes in ionization energy.
- The electron affinities of the alkaline earth metals become more negative from Be to Ba. The energy separation between the filled ns2 and the empty np subshells decreases with increasing n, so that formation of an anion from the heavier elements becomes energetically more favorable.
The equations for second and higher electron affinities are analogous to those for second and higher ionization energies:
\[E_{(g)} + e^- \rightarrow E^-_{(g)} \;\;\; \text{energy change=}EA_1 \label{7.5.5} \]
\[E^-_{(g)} + e^- \rightarrow E^{2-}_{(g)} \;\;\; \text{energy change=}EA_2 \label{7.5.6} \]
As we have seen, the first electron affinity can be greater than or equal to zero or negative, depending on the electron configuration of the atom. In contrast, the second electron affinity is always positive because the increased electron–electron repulsions in a dianion are far greater than the attraction of the nucleus for the extra electrons. For example, the first electron affinity of oxygen is −141 kJ/mol, but the second electron affinity is +744 kJ/mol:
\[O_{(g)} + e^- \rightarrow O^-_{(g)} \;\;\; EA_1=-141 \;kJ/mol \label{7.5.7} \]
\[O^-_{(g)} + e^- \rightarrow O^{2-}_{(g)} \;\;\; EA_2=+744 \;kJ/mol \label{7.5.8} \]
Thus the formation of a gaseous oxide (\(O^{2−}\)) ion is energetically quite unfavorable (estimated by adding both steps):
\[O_{(g)} + 2e^- \rightarrow O^{2-}_{(g)} \;\;\; EA=+603 \;kJ/mol \label{7.5.9} \]
Similarly, the formation of all common dianions (such as \(S^{2−}\)) or trianions (such as \(P^{3−}\)) is energetically unfavorable in the gas phase.
While first electron affinities can be negative, positive, or zero, second electron affinities are always positive.
Electron Affinity: Electron Affinity, YouTube(opens in new window) [youtu.be] (opens in new window)
If energy is required to form both positively charged cations and monatomic polyanions, why do ionic compounds such as \(MgO\), \(Na_2S\), and \(Na_3P\) form at all? The key factor in the formation of stable ionic compounds is the favorable electrostatic interactions between the cations and the anions in the crystalline salt.
Based on their positions in the periodic table, which of Sb, Se, or Te would you predict to have the most negative electron affinity?
Given: three elements
Asked for: element with most negative electron affinity
Strategy:
- Locate the elements in the periodic table. Use the trends in electron affinities going down a column for elements in the same group. Similarly, use the trends in electron affinities from left to right for elements in the same row.
- Place the elements in order, listing the element with the most negative electron affinity first.
Solution:
A We know that electron affinities become less negative going down a column (except for the anomalously low electron affinities of the elements of the second row), so we can predict that the electron affinity of Se is more negative than that of Te. We also know that electron affinities become more negative from left to right across a row, and that the group 15 elements tend to have values that are less negative than expected. Because Sb is located to the left of Te and belongs to group 15, we predict that the electron affinity of Te is more negative than that of Sb. The overall order is Se < Te < Sb, so Se has the most negative electron affinity among the three elements.
Based on their positions in the periodic table, which of Rb, Sr, or Xe would you predict to most likely form a gaseous anion?
- Answer
-
Rb
Summary
The electron affinity (EA) of an element is the energy change that occurs when an electron is added to a gaseous atom to give an anion. In general, elements with the most negative electron affinities (the highest affinity for an added electron) are those with the smallest size and highest ionization energies and are located in the upper right corner of the periodic table.

